Wykres wielomianu
Poziom rozszerzony
Zanim przystąpisz do rysowania wykresów wielomianów, musisz: - umieć rozkładać wielomiany na czynniki
- umieć rozwiązywać równania wielomianowe
- umieć określać krotności pierwiastków wielomianu
Do sprawdzania poprawności wykonanego wykresu możesz wykorzystywać program do rysowania wykresów funkcji.
Metoda rysowania wykresu wielomianu: - Przekształcamy wzór wielomianu do postaci iloczynowej.
- Wyznaczamy miejsca zerowe (pierwiastki) wielomianu.
- Określamy krotności wyliczonych pierwiastków oraz stopień wielomianu.
- Rysujemy wykres wielomianu od lewej strony do prawej według schematu:
- Rysujemy układ współrzędnych.
- Na osi x-ów zaznaczamy wyliczone miejsca zerowe.
- Określamy miejsce z którego zaczniemy rysować nasz wykres:
- Jeżeli stopień wielomianu jest parzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest dodatni, to zaczynamy rysowanie z lewego górnego rogu układu współrzędnych.
- Jeżeli stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest dodatni, to zaczynamy rysowanie z lewego dolnego rogu układu współrzędnych.
- Jeżeli stopień wielomianu jest parzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest ujemny, to zaczynamy rysowanie z lewego dolnego rogu układu współrzędnych.
- Jeżeli stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest ujemny, to zaczynamy rysowanie z lewego górnego rogu układu współrzędnych.
- Rysujemy linię wykresu do najbliższego miejsca zerowego.
Jeżeli dane miejsce zerowe ma krotność nieparzystą, to w tym miejscu wykres przebija oś x-ów.
Jeżeli miejsce zerowe ma krotność parzystą, to w tym miejscu wykres odbija się od osi x-ów. - Gdy już przejdziemy przez wszystkie miejsca zerowe, to kończymy rysowanie wykresu, pozwalając mu uciec do nieskończoności, po tej stronie osi x-ów, po której się znajduje.
Naszkicuj wykres wielomianu \(w(x) = x^2(x + 3)(x - 4)(x - 7)^3\).
Nasz wielomian dany jest już w postaci iloczynowej. Wyznaczamy zatem jego miejsca zerowe: \[ x^2(x + 3)(x - 4)(x - 7)^3 = 0\\[6pt] x = 0 \ \lor \ x + 3 = 0 \ \lor \ x - 4 = 0 \ \lor \ x - 7 = 0\\[6pt] x = 0 \ \lor \ x = -3 \ \lor \ x = 4 \ \lor \ x = 7\\[6pt] \] Teraz określamy krotności tych pierwiastków: 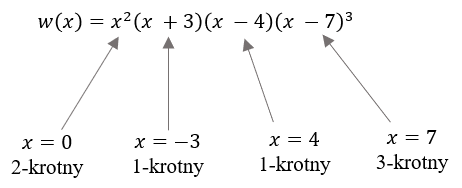 Wielomian \(w(x)\) jest \(7\) stopnia (bo suma wykładników \(2 + 1 + 1 + 3 = 7\)).
Wielomian \(w(x)\) jest \(7\) stopnia (bo suma wykładników \(2 + 1 + 1 + 3 = 7\)).
Ponadto współczynnik liczbowy przy \(x^7\) jest dodatni (jest równy \(1\)). W postaci iloczynowej nie widać bezpośrednio wyrażenia \(x^7\), ale łatwo zauważyć, że po wymnożeniu wszystkich nawiasów otrzymamy \(x^7\) ze współczynnikiem liczbowym równym \(1\).
Stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy \(x\) w najwyższej potędze jest dodatni, więc zaczynamy rysowanie wykresu od lewego dolnego rogu układu współrzędnych:
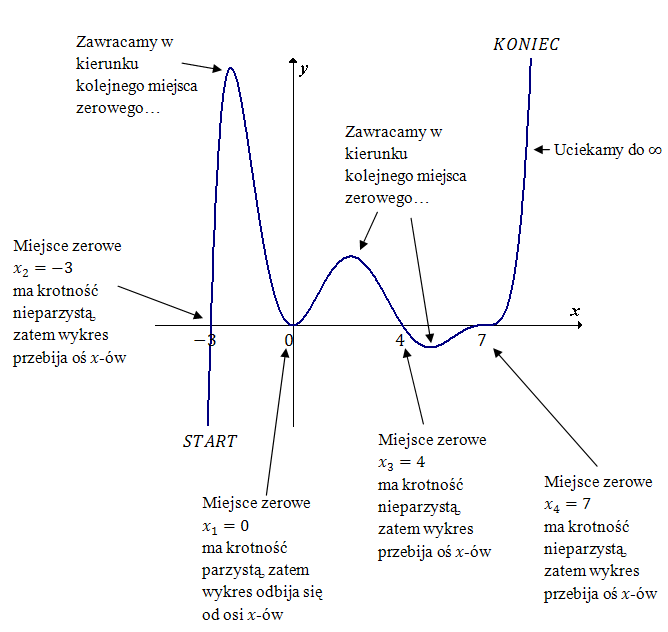 Uwaga
Uwaga
Wielkość "górek i dołków", czyli tych miejsc gdzie wykres zawraca, nie ma znaczenia. Można wszystkie rysować tej samej wielkości. Na powyższym wykresie górka między pierwszym, a drugim miejscem zerowym jest największa, bo tak w rzeczywistości wygląda ten wykres. My jednak nie musimy tego wiedzieć i moglibyśmy równie dobrze narysować ją dużo mniejszą.
 Wielomian \(w(x)\) jest \(7\) stopnia (bo suma wykładników \(2 + 1 + 1 + 3 = 7\)).
Wielomian \(w(x)\) jest \(7\) stopnia (bo suma wykładników \(2 + 1 + 1 + 3 = 7\)).Ponadto współczynnik liczbowy przy \(x^7\) jest dodatni (jest równy \(1\)). W postaci iloczynowej nie widać bezpośrednio wyrażenia \(x^7\), ale łatwo zauważyć, że po wymnożeniu wszystkich nawiasów otrzymamy \(x^7\) ze współczynnikiem liczbowym równym \(1\).
Stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy \(x\) w najwyższej potędze jest dodatni, więc zaczynamy rysowanie wykresu od lewego dolnego rogu układu współrzędnych:
 Uwaga
UwagaWielkość "górek i dołków", czyli tych miejsc gdzie wykres zawraca, nie ma znaczenia. Można wszystkie rysować tej samej wielkości. Na powyższym wykresie górka między pierwszym, a drugim miejscem zerowym jest największa, bo tak w rzeczywistości wygląda ten wykres. My jednak nie musimy tego wiedzieć i moglibyśmy równie dobrze narysować ją dużo mniejszą.
Naszkicuj wykres wielomianu \(W(x) = x^3 - 4x\).
Przekształcamy wielomian do postaci iloczynowej: \[\begin{split}W(x) &= x(x^2 - 4)\\[6pt] W(x) &= x(x - 2)(x + 2)\end{split}\] Teraz wyznaczamy miejsca zerowe: \[x(x - 2)(x + 2) = 0\\[6pt] x = 0 \quad \lor \quad x - 2 = 0 \quad \lor \quad x + 2 = 0\\[6pt] x = 0 \quad \lor \quad x = 2 \quad \lor \quad x = -2 \] Teraz określamy krotności tych pierwiastków: 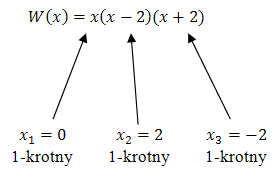


Nasz wielomian jest stopnia \(3\), a współczynnik liczbowy przy \(x^3\) jest dodatni (jest równy dokładnie \(1\)).
Stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy \(x\) w najwyższej potędze jest dodatni, więc zaczynamy rysowanie wykresu od lewego dolnego rogu układu współrzędnych: 
Naszkicuj wykres wielomianu \(W(x) = -6x^3 + 18x\).
Przekształcamy wielomian do postaci iloczynowej: \[\begin{split}W(x) &= -6x(x^2 - 3)\\[6pt] W(x) &= -6x(x - \sqrt{3})(x + \sqrt{3}) \end{split}\] Teraz wyznaczamy miejsca zerowe: \[ -6x(x - \sqrt{3})(x + \sqrt{3}) = 0\\[6pt] x = 0 \quad \lor \quad x - \sqrt{3} = 0 \quad \lor \quad x + \sqrt{3} = 0\\[6pt] x = 0 \quad \lor \quad x = \sqrt{3} \quad \lor \quad x = -\sqrt{3} \] Teraz określamy krotności tych pierwiastków: 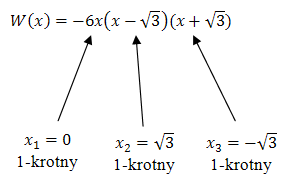

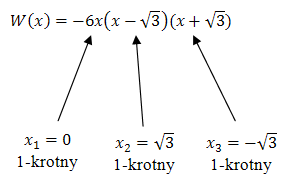
Nasz wielomian jest stopnia \(3\), a współczynnik liczbowy przy \(x^3\) jest ujemny (jest równy dokładnie \(-6\)).
Stopień wielomianu jest nieparzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest ujemny, więc zaczynamy rysowanie wykresu od lewego górnego rogu układu współrzędnych: 
Naszkicuj wykres wielomianu \(W(x) = (x + 4)^2(x + 1)(x - 3)\).
Wielomian jest dany w postaci iloczynowej, więc zaczynamy od wyznaczenia miejsc zerowych: \[ (x + 4)^2(x + 1)(x - 3) = 0\\[6pt] x + 4 = 0 \quad \lor \quad x + 1 = 0 \quad \lor \quad x - 3 = 0\\[6pt] x = -4 \quad \lor \quad x = -1 \quad \lor \quad x = 3 \] Teraz określamy krotności tych pierwiastków: 
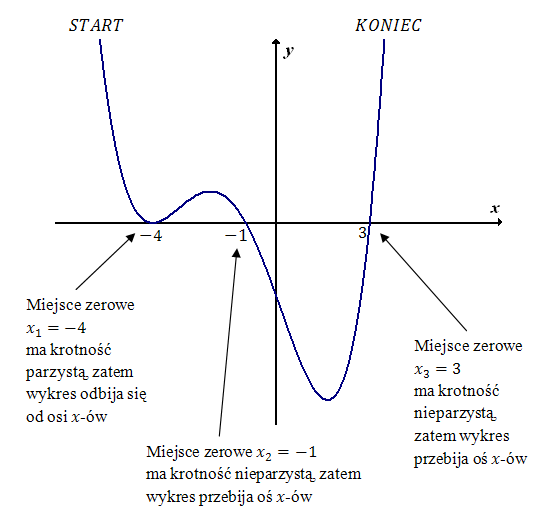

Nasz wielomian jest stopnia \(4\), a współczynnik liczbowy przy \(x^4\) (po wymnożeniu nawiasów) jest dodatni (jest równy dokładnie \(1\)).
Stopień wielomianu jest parzysty oraz współczynnik liczbowy przy x w najwyższej potędze jest dodatni, więc zaczynamy rysowanie wykresu od lewego górnego rogu układu współrzędnych: 
Naszkicuj wykres wielomianu \(W(x) = -2(x + 7)^2(x + 3)^3(x - 1)^4(x - 3)^5(x - 6)^2\).
Wielomian jest dany w postaci iloczynowej, więc zaczynamy od wyznaczenia miejsc zerowych: \[-2(x + 7)^2(x + 3)^3(x - 1)^4(x - 3)^5(x - 6)^2 = 0\\[6pt] x + 7 = 0 \quad \lor \quad x + 3 = 0 \quad \lor \quad x - 1 = 0 \quad \lor \quad x - 3 = 0 \quad \lor \quad x - 6 = 0\\[6pt] x = -7 \quad \lor \quad x = -3 \quad \lor \quad x = 1 \quad \lor \quad x = 3 \quad \lor \quad x = 6 \] Teraz określamy krotności tych pierwiastków: 


Nasz wielomian jest stopnia \(16\), a współczynnik liczbowy przy \(x^{16}\) (po wymnożeniu nawiasów) jest ujemny (jest równy dokładnie \(-2\)).
Stopień wielomianu jest parzysty oraz współczynnik liczbowy przy \(x\) w najwyższej potędze jest ujemny, więc zaczynamy rysowanie wykresu od lewego dolnego rogu układu współrzędnych: 
Tematy nadrzędne i sąsiednie