Nierówności wielomianowe

Poziom rozszerzony

Zanim przystąpisz do rozwiązywania nierówności wielomianowych, musisz umieć:

Nierówności wielomianowe rozwiązujemy rysując wykres wielomianu i odczytując z niego rozwiązanie.

Oto przykładowe nierówności wielomianowe:

\(6x^2 + 10x - 1 \lt 0\)

\(x^4 + x^2 - 6x - 10 \le 0\)

\(x^6 + 4x^3 - 2 \gt 0\)

\(x^7 \ge 2x^3 + x\)

Nierówności wielomianowe drugiego stopnia (czyli tzw. nierówności kwadratowe) rozwiązujemy metodami opisanymi na tej stronie.

Metoda rozwiązywania nierówności \(3\) stopnia i wyższych

Przenosimy wszystkie wyrażenia na lewą stronę nierówności, tak aby po prawej stronie zostało zero.
Od tego momentu lewą stronę nierówności traktujemy jako wzór wielomianu, którego wykres będziemy chcieli naszkicować.
Wyznaczamy miejsca zerowe otrzymanego wielomianu.
Rysujemy wykres wielomianu i odczytujemy z niego rozwiązanie.

Rozwiąż nierówność \(x^3 + 5x^2 \lt 4x + 20\).

Przenosimy wszystkie wyrazy na lewą stronę: \[x^3 + 5x^2 - 4x - 20 \lt 0\] Lewą stronę naszej nierówności traktujemy jako wielomian: \[W(x) = x^3 + 5x^2 - 4x - 20\] Teraz musimy wyznaczyć miejsca zerowe tego wielomianu. W tym celu rozwiązujemy równanie: \[\begin{split} x^3 + 5x^2 - 4x - 20 &= 0\\[6pt] x^2(x + 5) - 4(x + 5) &= 0\\[6pt] (x + 5)(x^2 - 4) &= 0\\[6pt] (x + 5)(x - 2)(x + 2) &= 0\\[6pt] x + 5 = 0 \quad \lor \quad x - 2 = 0 \quad &\lor \quad x + 2 = 0\\[6pt] x = -5 \quad \lor \quad x = 2 \quad &\lor \quad x = -2 \end{split}\] Mamy już wyliczone miejsca zerowe wielomianu \(W(x)\). Możemy zatem naszkicować wykres tego wielomianu:

Wracamy teraz do naszej nierówności i patrzymy na jej znak: \[x^3 + 5x^2 - 4x - 20 \lt 0\] W tej nierówności występuje znak mniejszości (\(\lt\)), zatem jej rozwiązaniem będzie zbiór tych wszystkich argumentów \(x\), dla których wykres wielomianu jest poniżej osi \(x\)-ów.
Zaznaczamy na wykresie odpowiednie przedziały:

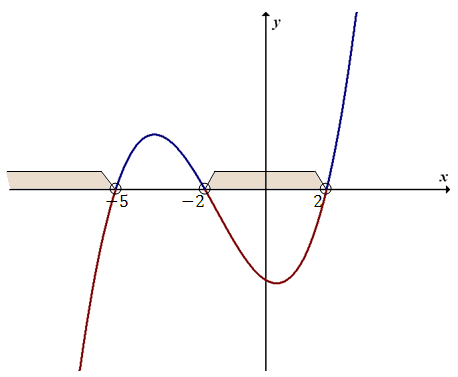Rozwiązaniem naszej nierówności jest zbiór: \[x \in (-\infty; -5) \cup (-2; 2)\]

Rozwiąż nierówność \(x^3 + 3x^2 - 3x - 9 \lt 0\).

Lewą stronę naszej nierówności traktujemy jako wielomian: \[W(x) = x^3 + 3x^2 - 3x - 9\] Wyznaczamy miejsca zerowe tego wielomianu, rozwiązując równanie: \[\begin{split} x^3 + 3x^2 - 3x - 9 &= 0\\[6pt] x^2(x + 3) - 3(x + 3) &= 0\\[6pt] (x + 3)(x^2 - 3) &= 0\\[6pt] (x + 3)(x - \sqrt{3})(x + \sqrt{3}) &= 0\\[6pt] x + 3 = 0 \quad \lor \quad x - \sqrt{3} = 0 \quad &\lor \quad x + \sqrt{3} = 0\\[6pt] x = -3 \quad \lor \quad x = \sqrt{3} \quad &\lor \quad x = -\sqrt{3} \end{split}\] Mamy już wyliczone miejsca zerowe wielomianu \(W(x)\). Możemy zatem naszkicować wykres tego wielomianu:

Patrzymy teraz na znak w naszej nierówności. Jest to znak mniejszości (\(\lt\)). Zaznaczamy zatem ten fragment wykresu, który znajduje się pod osią \(x\)-ów. Od razu zaznaczamy również odpowiednie przedziały na osi \(x\)-ów dla tych fragmentów wykresu.

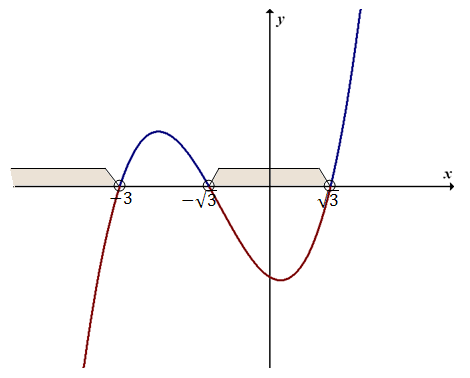Zapisujemy zbiór rozwiązań nierówności: \[x \in (-\infty; -3) \cup (-\sqrt{3}; \sqrt{3})\]

Rozwiąż nierówność \((-x - 2)(x - 3)(x - 6) \le 0\).

Lewą stronę naszej nierówności traktujemy jako wielomian: \[W(x) = (-x - 2)(x - 3)(x - 6)\] Wyznaczamy miejsca zerowe tego wielomianu, rozwiązując równanie: \[\begin{split} (-x - 2)(x - 3)(x - 6) &= 0\\[6pt] -x - 2 = 0 \quad \lor \quad x - 3 = 0 \quad &\lor \quad x - 6 = 0\\[6pt] x = -2 \quad \lor \quad x = 3 \quad &\lor \quad x = 6 \end{split}\] Mamy już wyliczone miejsca zerowe wielomianu \(W(x)\). Możemy zatem naszkicować wykres tego wielomianu: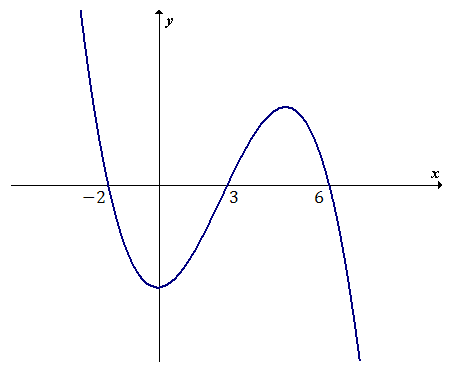

Patrzymy teraz na znak w naszej nierówności. Jest to znak mniejszości bądź równości (\(\le\)). Zaznaczamy zatem ten fragment wykresu, który znajduje się pod osią \(x\)-ów, wraz z miejscami zerowymi. Zaznaczamy również przedziały na osi \(x\)-ów, dla tych fragmentów wykresu.

Zapisujemy zbiór rozwiązań nierówności: \[x ∈ \langle -2; 3\rangle \cup \langle 6; +\infty )\]

Rozwiąż nierówność \(-3x^3 + 15x \gt 0\).

Lewą stronę naszej nierówności traktujemy jako wielomian: \[W(x) = -3x^3 + 15x\] Wyznaczamy miejsca zerowe tego wielomianu, rozwiązując równanie: \[\begin{split} -3x^3 + 15x &= 0\\[6pt] -3x(x^2 - 5) &= 0\\[6pt] -3x(x - \sqrt{5})(x + \sqrt{5}) &= 0\\[6pt] x = 0 \quad \lor \quad x - \sqrt{5} = 0 \quad &\lor \quad x + \sqrt{5} = 0\\[6pt] x = 0 \quad \lor \quad x = \sqrt{5} \quad &\lor \quad x = -\sqrt{5} \end{split}\] Mamy już wyliczone miejsca zerowe wielomianu \(W(x)\). Możemy zatem naszkicować wykres tego wielomianu: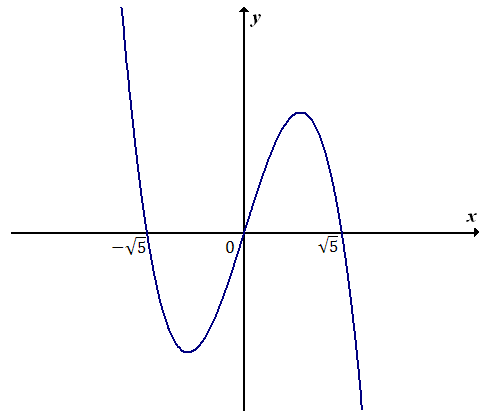

Patrzymy teraz na znak w naszej nierówności. Jest to znak większości (\(\gt\)). Zaznaczamy zatem ten fragment wykresu, który znajduje się nad osią \(x\)-ów. Od razu zaznaczamy również odpowiednie przedziały na osi \(x\)-ów dla tych fragmentów wykresu.

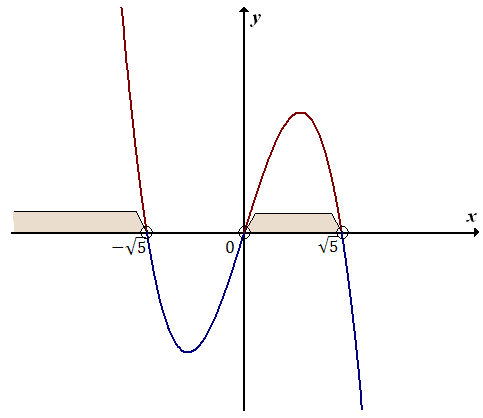Zapisujemy zbiór rozwiązań nierówności: \[x \in (-\infty; -\sqrt{5}) \cup (0; \sqrt{5})\]

Jedną z liczb spełniających nierówność \((x-6)\cdot (x-2)^2\cdot (x+4)\cdot (x+10)\gt0\) jest

A.\( -5 \)

B.\( 0 \)

C.\( 3 \)

D.\( 5 \)

Na rysunku poniżej przedstawiono fragment wykresu funkcji liniowej \(f(x)=-2x+2\) oraz fragment wykresu wielomianu \(w(x)=x^4-6x^3+8x^2+4x-7\). Rozwiąż nierówność \(w(x)\ge f(x)\).

\(x\in (-\infty ,-1\rangle \cup \langle 1,+\infty )\)

Na rysunku przedstawiono fragment wykresu wielomianu \(W(x)=\frac{1}{2}x^4+\frac{3}{2}x^3-4x^2-6x+8\). Wielomian \(W\) jest podzielny przez dwumian \(\frac{1}{2}x+2\). Rozwiąż nierówność \(W(x+2)\ge 0\).

\(x\in (-\infty ,-6\rangle \cup \langle -4,-1 \rangle \cup \langle 0,+\infty ) \)

Wielomian określony wzorem \(W(x) = 2x^3 + (m^3 + 2)x^2 - 11x - 2(2m + 1)\) jest podzielny przez dwumian \((x - 2)\) oraz przy dzieleniu przez dwumian \((x + 1)\) daje resztę \(6\). Oblicz \(m\) i dla wyznaczonej wartości \(m\) rozwiąż nierówność \(W(x) \le 0\).

\(x \in (-\infty, -3\bigl] \cup \biggl[-\frac{1}{2}, 2\biggl]\)

Reszta z dzielenia wielomianu \(W(x)=4x^3-6x^2-(5m+1)x-2m\) przez dwumian \(x+2\) jest równa \((−30)\). Oblicz \(m\) i dla wyznaczonej wartości \(m\) rozwiąż nierówność \(W(x)\ge 0\).

\(x\in \left\langle -1,-\frac{1}{2} \right\rangle\cup \langle 3,+\infty ) \)