Nierówności kwadratowe

Poziom podstawowy

Nierówność kwadratowa - to nierówność, którą można zapisać w postaci: \[ax^2+bx+c\lt 0\] gdzie \(a, b, c \in \mathbb{R} \) i \(a\ne 0\).
Znak nierówności może być dowolny spośród: \(\lt, \leqslant, \gt, \geqslant \).

Metoda rozwiązywania nierówności kwadratowej

Żeby rozwiązać nierówność kwadratową \(ax^2+bx+c\lt 0\), to należy:

wyznaczyć miejsca zerowe funkcji kwadratowej \(f(x)=ax^2+bx+c\ \) (o ile istnieją),
naszkicować wykres funkcji \(f(x)\),
odczytać z wykresu rozwiązanie nierówności.

Rozwiąż nierówność \(x^2 + 4x + 3 \lt 0\).

Lewą stronę nierówności traktujemy jak funkcję kwadratową: \[f(x) = x^2 + 4x + 3\] Wyznaczamy miejsca zerowe tej funkcji. Najpierw liczymy deltę: \[ \Delta = 4^2 - 4 \cdot 1 \cdot 3 = 16 - 12 = 4 \] Czyli: \[\sqrt{\Delta} = 2\] Zatem miejsca zerowe, to: \[\begin{split} x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-4-2}{2\cdot 1}=-3\\[6pt] x_2=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-4+2}{2\cdot 1}=-1 \end{split}\] Teraz szkicujemy wykres paraboli: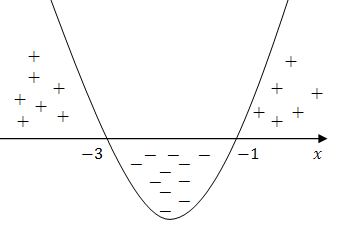

Ramiona paraboli będą skierowane do góry, ponieważ współczynnik liczbowy przy \(x^2\) jest dodatni.

Z rysunku odczytujemy, że parabola przyjmuje wartości mniejsze od zera dla: \[x \in (-3, -1)\]

Rozwiąż nierówność \(x^2 + 4x + 3 \le 0\).

Ten przykład różni się od poprzedniego jedynie znakiem nierówności. W tym przypadku rozwiązaniem są te wszystkie \(x\)-y dla których parabola jest ujemna lub równa zero, czyli: \[x \in \langle -3, -1\rangle \]

Rozwiąż nierówność \(x^2 + 4x + 3 \gt 0\).

Ten przykład różni się od poprzedniego jedynie znakiem nierówności. W tym przypadku rozwiązaniem są te wszystkie \(x\)-y dla których parabola przyjmuje wartości dodatnie, czyli: \[x \in (-\infty ,-3)\cup (-1,+\infty ) \]

Rozwiąż nierówność \(x^2 + 4x + 3 \ge 0\).

Ten przykład różni się od poprzedniego jedynie znakiem nierówności. W tym przypadku rozwiązaniem są te wszystkie \(x\)-y dla których parabola jest dodatnia lub równa zero, czyli: \[x \in (-\infty ,-3\rangle \cup \langle -1,+\infty ) \]

Szybka nawigacja do zadania numer: 5 10 15 20 25 30 35 .

Na filmie pokazuję wszystkie możliwe typy nierówności kwadratowych oraz sposoby ich rozwiązywania.

Czas nagrania: 27 min.

Rozwiąż nierówność \(-2x^2 + 0{,}5x \ge 0\).

\(x\in \left\langle 0;\frac{1}{4} \right\rangle \)

Rozwiąż nierówność: \(-x^2+2x+8\ge 0\).

\(x\in \langle -2,4\rangle \)

Zbiorem rozwiązań nierówności \(x^2\lt 4\) jest

A.\( (-2;2) \)

B.\( (-\infty ;-2)\cup (2;\infty ) \)

C.\( (-\infty ;2) \)

D.\( \langle -2;2 \rangle \)

Rozwiąż nierówność \(x^2+6x-7\le 0\).

\(x\in \left\langle -7; 1 \right\rangle \)

Rozwiąż nierówność \(x^2-9>0\).

\(x\in (-\infty ;-3)\cup (3;+\infty )\)

Zbiorem rozwiązań nierówności \(x(x+6)\lt 0\) jest

A.\( (-6,0) \)

B.\( (0,6) \)

C.\( (-\infty ,-6)\cup (0,+\infty ) \)

D.\( (-\infty ,0)\cup (6,+\infty ) \)

Rozwiąż nierówność \(x^2-8x+7\ge 0\).

\(x\in (-\infty ;1\rangle \cup \langle 7;+\infty )\)

Rozwiąż nierówność \(x^2 - 3x - 10 \lt 0\).

\(x\in (-2,5)\)

Rozwiąż nierówność \(x^2 + 8x + 15 > 0\).

\(x\in (-\infty ;-5) \cup (-3;+\infty )\)

Rozwiąż nierówność \(-2x^2+3x+2\le 0\) .

\(x\in \left(-\infty ;-\frac{1}{2}\right\rangle \cup \langle 2;+\infty )\)

Rozwiąż nierówność \(-3x^2 + 3x + 36 \ge 0\) .

\(x\in \langle -3; 4 \rangle \)

Do zbioru rozwiązań nierówności \((x-2)(x+3)\lt 0\) należy liczba

A.\( 9 \)

B.\( 7 \)

C.\( 4 \)

D.\( 1 \)

Rozwiąż nierówność \(x^2 - x - 2 \le 0\).

\(x\in \langle -1; 2\rangle \)

Do zbioru rozwiązań nierówności \(9\le x^2\) należy liczba

A.\( -2 \)

B.\( 0 \)

C.\( -3 \)

D.\( 2 \)

Rozwiąż nierówność \(x^2 + 5x \le 6\).

\(x\in \langle -6; 1 \rangle \)

Rozwiąż nierówność \(x^2 - 3x + 2 \lt 0\).

\(x\in (1;2)\)

Zbiorem rozwiązań nierówności \(x^2 > 4x\) jest

A.\( (-\infty ,-4)\cup (0,+\infty ) \)

B.\( (4,+\infty ) \)

C.\( (-\infty ,-2)\cup (2,+\infty ) \)

D.\( (-\infty ,0)\cup (4,+\infty ) \)

Rozwiąż nierówność \(x^2-x+5>0\).

\(x\in \mathbb{R} \)

Zbiorem rozwiązań nierówności \(\ 3x^2+2x-1 \le 0\ \) jest

A.\( (-\infty ,-1)\cup \left \langle \frac{1}{3},+\infty \right ) \)

B.\( \left (-1,\frac{1}{3} \right ) \)

C.\( (-\infty ,-1)\cup \left (\frac{1}{3},+\infty \right ) \)

D.\( \left \langle -1,\frac{1}{3} \right \rangle \)

Zbiorem rozwiązań nierówności \(-x^2+2x-1 \lt 0\) jest

A.zbiór pusty

B.\( \mathbb{R} \backslash \{ 1 \} \)

C.\( \mathbb{R} \)

D.\( \mathbb{R} \backslash \{ -1 \} \)

Zbiorem rozwiązań nierówności \((x-2)(x+3) \ge 0\) jest

A.\( \langle -2, 3 \rangle \)

B.\( \langle -3, 2 \rangle \)

C.\( ( -\infty , -3 \rangle \cup \langle 2, +\infty ) \)

D.\( ( -\infty , 2 \rangle \cup \langle 3, +\infty ) \)

Rozwiąż nierówność \(x^2+11x+30 \le 0\).

\(x\in \langle -6;-5 \rangle \)

Zbiorem rozwiązań nierówności \(\ x(x+5)>0\ \) jest

A.\( (-\infty, 0)\cup (5, +\infty ) \)

B.\( (-\infty, -5)\cup (0, +\infty ) \)

C.\( (-\infty, -5)\cup (5, +\infty ) \)

D.\( (-5, +\infty ) \)

Rozwiąż nierówność \(x^2−14x+24 \gt 0\).

\(x\in (-\infty ;2)\cup (12;+\infty )\)

Rozwiąż nierówność \(2x^2-7x+5 \ge 0\).

\(x\in (-\infty ;1\rangle \cup \langle 2{,}5; +\infty )\)

Rozwiąż nierówność \(3x-x^2 \ge 0\).

\(x\in \langle 0;3 \rangle \)

Rozwiąż nierówność: \(-2x^2+3x\lt 4\).

\(x\in \mathbb{R} \)

Najmniejszą liczbą naturalną, która nie spełnia nierówności \( x^2-7x-5\lt 0 \) jest:

A.\(0 \)

B.\(3 \)

C.\(7 \)

D.\(8 \)

Wyznacz wszystkie liczby naturalne spełniające nierówność \( x^2-x-12\leqslant 0 \).

\(x\in \{1,2,3,4\} \) lub ewentualnie \(x\in \{0,1,2,3,4\} \) jeżeli \(0\) uznajemy za liczbę naturalną.

Rozwiąż nierówność \( (2-x)^2 \le 9 \).

\(x\in \langle -1;5 \rangle \)

Rozwiąż nierówność \( -x^2-5x+14\lt 0 \).

\(x\in (-\infty ;-7)\cup (2;+\infty )\)

Rozwiąż nierówność: \( -x^2-4x+21\lt 0 \).

\(x\in (-\infty ;-7)\cup (3;+\infty )\)

Rozwiąż nierówność \(2x^2-4x\gt (x+3)(x-2)\).

\(x\in (-\infty ;2)\cup (3;+\infty )\)

Rozwiąż nierówność \(2x^2-4x\ge x-2\).

\(x\in \left(-\infty ;\frac{1}{2}\right\rangle \cup \langle 2;+\infty ) \)

Rozwiąż nierówność \(20x \ge 4x^2 + 24\).

\(x\in \langle 2;3\rangle \)

Rozwiąż nierówność \(5x^2 − 45 \le 0\).

\(x\in \langle -3;3\rangle \)