Określamy kwadraty \(K_1, K_2, K3_,...\) następująco: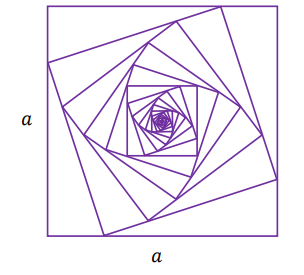

• \(K_1\) jest kwadratem o boku długości \(a\)
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1 ∶ 3\)
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1 ∶ 3\)

i ogólnie, dla każdej liczby naturalnej \(n \ge 2\),

• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_{n-1}\) i dzieli ten bok w stosunku \(1 ∶ 3\).

Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.