Matura rozszerzona - zbiór zadań - szeregi geometryczne

Dany jest ciąg geometryczny \((a_n)\) określony wzorem \(a_n=\left(\frac{1}{2x-371}\right )^n\) dla \(n\ge 1\). Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą \(x\), dla której nieskończony szereg \(a_1+a_2+a_3+...\) jest zbieżny.

Pierwszy wyraz \(a_1\) nieskończonego ciągu geometrycznego \((a_n)\) jest równy \(\sqrt{2}\), natomiast suma pierwszych trzech jego wyrazów jest równa \(\frac{7}{4}\sqrt{2}\). Szereg nieskończony \(a_1+a_2+a_3+...\) jest zbieżny. Oblicz jego sumę.

Dany jest nieskończony ciąg geometryczny \((a_n)\) zbieżny o pierwszym wyrazie dodatnim. Wykaż, że suma wszystkich wyrazów tego ciągu o numerach nieparzystych jest większa lub równa od czterokrotności trzeciego wyrazu ciągu \((a_n)\).

Dany jest nieskończony ciąg sześcianów. Krawędź pierwszego z nich jest równa \(x_1\). Krawędź drugiego z tych sześcianów ma długość \(x_2\) równą różnicy długości przekątnej pierwszego sześcianu i przekątnej ściany pierwszego sześcianu. Analogicznie trzeci sześcian ma krawędź \(x_3\) o długości równej różnicy długości przekątnej drugiego sześcianu i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę \(x_1+x_2+x_3+...\).

Funkcja \(f\), której dziedziną jest zbiór \((1,+\infty )\), jest określona wzorem \[f(x)=x+1+\frac{x+1}{x}+\frac{x+1}{x^2}+\frac{x+1}{x^3}+...\] Wyznacz wszystkie argumenty, dla których funkcja \(f\) przyjmuje wartość \(6\).

Określamy kwadraty \(K_1, K_2, K3_,...\) następująco: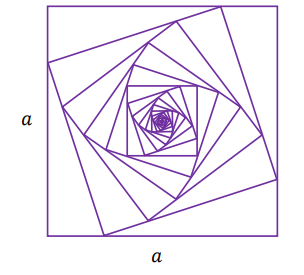

• \(K_1\) jest kwadratem o boku długości \(a\)
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1 ∶ 3\)
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1 ∶ 3\)

i ogólnie, dla każdej liczby naturalnej \(n \ge 2\),

• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_{n-1}\) i dzieli ten bok w stosunku \(1 ∶ 3\).

Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.

Dany jest nieskończony szereg geometryczny \[2x-\frac{6x}{x-1}+\frac{18x}{(x-1)^2}-\frac{54x}{(x-1)^3}+\ ...\]

Rozwiąż nierówność \(\frac{1}{x-3}+\frac{1}{(x-3)^2}+\frac{1}{(x-3)^3}+...\ge2-x\), gdzie lewa strona nierówności jest szeregiem geometrycznym zbieżnym. Podaj odpowiednie założenia.