Pewniaki do matury rozszerzonej 2026
Poziom rozszerzony
Pewniaki do matury rozszerzonej 2026!
Strona zawiera typy zadań, które mają największą szansę pojawić się na maturze rozszerzonej w nowej formule w roku 2026.
Strona zawiera typy zadań, które mają największą szansę pojawić się na maturze rozszerzonej w nowej formule w roku 2026.
Jak wybrałem pewniaki?
Pewniaki to są typy zadań, które pojawiały się najczęściej we wszystkich ostatnich oficjalnych arkuszach i materiałach od CKE i są zgodne z najnowszymi wymaganiami.
Pewniaki to są typy zadań, które pojawiały się najczęściej we wszystkich ostatnich oficjalnych arkuszach i materiałach od CKE i są zgodne z najnowszymi wymaganiami.
Pełną wiedzę niezbędną do zdania matury na 100% znajdziesz w kursie do nowej matury rozszerzonej.
Spis zagadnień
Wyjaśnienie oznaczeń:- Wytłuszczone – typowe zagadnienia, które prawie na pewno pojawią się na maturze (szansa ponad 90%) i które względnie łatwo opanować.
- Niewytłuszczone, bez gwiazdek – zagadnienia które prawie na pewno pojawią się na maturze (szansa ponad 80%), ale które mają więcej różnorodnych typów zadań i które trochę trudniej opanować.
- Zagadnienia z * – to grupa tematów z których przynajmniej jeden na pewno pojawi się na maturze.
- Zagadnienia z ** – tematy z małą szansą pojawienia się na maturze.
Dodatkowe uwagi:
- W zagadnieniach 1 - 8 mamy typowe pewniaki - konkretne typy zadań - dosyć schematyczne i względnie łatwe w opanowaniu.
- W zagadnieniach 9 - 10 mamy zagadnienia z geometrii bez konkretnych typów zadań. Ciężko wskazać w geometrii konkretne typy zadań, ponieważ mam tutaj dużo różnych możliwości.
- W zagadnieniach 11 - 12 mamy zagadnienia z kombinatoryki i rachunku prawdopodobieństwa. Na pewno coś z tego będzie na maturze. Może pojawić się też zwykłe prawdopodobieństwo warunkowe.
- W zagadnieniach 13 - 15 mamy typowe zadania z badania funkcji. Jest bardzo duża szansa, że któreś z tych zadań pojawi się na maturze, ale raczej nie wszystkie trzy na raz. Zatem zagadnienia 13 14 i 15 można traktować w sumie jako jednego pewniaka (szansa powyżej 90%).
Zamiana podstaw logarytmów [2-3 punkty]
Dane są liczby \[a=4^{\log_245}\ \ \ \text{oraz}\ \ \ b=\frac{\log_32023}{\log_92023}\]
Oblicz \(a-b\).
Dane są liczby \(a = \log_23\) oraz \(b = \log_37\).
Wyraź \(\log_449\) za pomocą liczb \(a\) oraz \(b\).
Zapisz obliczenia.
Wykaż, że \[ \frac{1}{\log _{2} 35+1}+\frac{1}{\log _{7} 140-\log _{7} 2}+\frac{1}{\log _{5} 7+\log _{5} 2+1}=1 \]
Równanie kwadratowe z parametrem [5 punktów]
Dane jest równanie \((x - 6) ⋅ \bigl[(m - 2)x^2 - 4(m + 3)x + m + 1\bigl] = 0\) z niewiadomą \(x\) i parametrem \(m\in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(m\), dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\ne 2\), dla których równanie \[x^2+4x-\frac{m-3}{m-2}=0\] ma dwa różne rozwiązania rzeczywiste \(x_1, x_2\) spełniające warunek \(x_1^3+x_2^3\gt-28\). Zapisz obliczenia.
Wyznacz wszystkie wartości parametru \(m\), dla których równanie \[mx^2-(m+1)x-2m+3=0\] ma dokładnie dwa różne rozwiązania rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \[x_1\ne 0, \ \ \ x_2\ne 0\ \ \ \text{oraz}\ \ \ \frac{1}{x_1^2}+\frac{1}{x_2^2} \lt 1\] Zapisz obliczenia.
Równanie trygonometryczne [3-4 punkty]
Rozwiąż równanie \[4\sin(4x)\cos(6x)=2\sin(10x)+1\]
Rozwiąż równanie \[\sin (3x)=2\sin x\] w zbiorze \([0,\pi ]\).
Rozwiąż równanie \[ \sin ^{4} x=\sin x \cdot \cos x-\cos ^{4} x \] w zbiorze \([-\pi, 2 \pi]\). Zapisz obliczenia.
Rozwiąż równanie \[\sin(5x)+\cos x=0\] w zbiorze \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\). Zapisz obliczenia.
Rozwiąż równanie \[ \sin (6 x)+\sqrt{3} \cdot \sin (5 x)+\sin (4 x)=0 \] Zapisz obliczenia.
Funkcja wykładnicza w praktyce [2 punkty]
W chwili początkowej \((t=0)\) zainicjowano pewną reakcję chemiczną, w której brał udział związek A.
W wyniku tej reakcji masa \(m\) związku A zmieniała się w czasie zgodnie z zależnością \[ m(t)=a \cdot 2^{-0,05 \cdot t}+b \quad \text { dla } \quad t \geq 0 \] gdzie:
\(m\) - masa związku A wyrażona w gramach,
\(t\) - czas wyrażony w sekundach (liczony od chwili \(t=0\) ),
\(a, b\) - współczynniki liczbowe.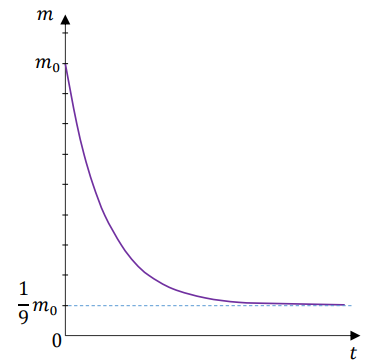
W wyniku tej reakcji masa \(m\) związku A zmieniała się w czasie zgodnie z zależnością \[ m(t)=a \cdot 2^{-0,05 \cdot t}+b \quad \text { dla } \quad t \geq 0 \] gdzie:
\(m\) - masa związku A wyrażona w gramach,
\(t\) - czas wyrażony w sekundach (liczony od chwili \(t=0\) ),
\(a, b\) - współczynniki liczbowe.
Masa początkowa związku A (tj. masa w chwili \(t=0\) ) była równa \(m_{0}\) gramów.
Po osiągnięciu stanu równowagi (tj. gdy \(t \rightarrow \infty\) ) masa tego związku była równa \(\frac{1}{9}\) jego masy początkowej (zobacz rysunek).
Po osiągnięciu stanu równowagi (tj. gdy \(t \rightarrow \infty\) ) masa tego związku była równa \(\frac{1}{9}\) jego masy początkowej (zobacz rysunek).

Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało \(87,5 \%\) masy początkowej tego związku. Zapisz obliczenia.
Ładunek elektryczny zgromadzony w kondensatorze można opisać zależnością \[ Q(t)=Q_{0} \cdot \beta^{-t} \quad \text { dla } \quad t \geq 0 \] gdzie:
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.
Wiadomo, że w chwili \(t=4 \mathrm{~s}\) w kondensatorze był zgromadzony ładunek \(2\) milikulombów, a w chwili \(t=6 \mathrm{~s}\) - ładunek \(18\) milikulombów.
Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili \(t=5 \mathrm{~s}\). Zapisz obliczenia.
Zadanie optymalizacyjne [6 punktów]
Funkcja \(f\) jest określona wzorem \(f(x) = 81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\) dla każdej liczby dodatniej \(x\).
Wykaż, że dla każdej liczby dodatniej \(x\) wyrażenie \[81^{\log_3x}+\frac{2\cdot \log_2\sqrt{27}\cdot \log_32}{3}\cdot x^2-6x\] można równoważnie przekształcić do postaci \(x^4+x^2-6x\).
Oblicz najmniejszą wartość funkcji \(f\) określonej dla każdej liczby dodatniej \(x\). Zapisz obliczenia.
Wskazówka: przyjmij, że wzór funkcji \(f\) można przedstawić w postaci \(f(x) = x^4 + x^2 - 6x\).
Dana jest kula o promieniu \(1\). Rozpatrujemy wszystkie stożki zawierające środek kuli i wpisane w tę kulę, to znaczy takie, w których: 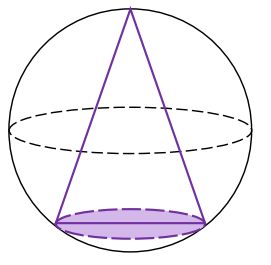
- wierzchołek leży na powierzchni kuli
- okrąg, będący krawędzią podstawy stożka, leży na powierzchni kuli (zobacz rysunek).

Oblicz promień podstawy tego stożka, który ma największą objętość. Oblicz objętość tego stożka. Zapisz obliczenia.
Ciąg arytmetyczny i geometryczny [4-5 punktów]
Trzywyrazowy ciąg \((x, y, z)\) jest geometryczny i rosnący. Suma wyrazów tego ciągu jest równa \(105\). Liczby \(x, y\) oraz \(z\) są - odpowiednio - pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego \(\left(a_{n}\right)\), określonego dla każdej liczby naturalnej \(n \geq 1\).
Oblicz \(x, y\) oraz z. Zapisz obliczenia.
Nieskończony ciąg geometryczny \((a_{n})\) jest określony dla każdej liczby naturalnej \(n \geq 1\). Suma wszystkich wyrazów ciągu \((a_{n})\) o numerach nieparzystych jest równa \(16\), tj. \[ a_{1}+a_{3}+a_{5}+\ldots=16 \] Ponadto \(a_{1}+a_{3}=\frac{5}{2} \cdot a_{2}\).
Wyznacz wzór ogólny na \(n\)-ty wyraz ciągu \((a_{n})\). Zapisz obliczenia.
Trzeci i piąty wyraz malejącego ciągu arytmetycznego \((a_{n})\), określonego dla każdej liczby naturalnej \(n \geq 1\), spełniają warunek \(a_{3}+a_{5}=10\).
Trzywyrazowy ciąg ( \(2 a_{1}+4, a_{4}-1,-\frac{1}{8} a_{7}\) ) jest geometryczny.
Trzywyrazowy ciąg ( \(2 a_{1}+4, a_{4}-1,-\frac{1}{8} a_{7}\) ) jest geometryczny.
Oblicz wyrazy tego ciągu geometrycznego. Zapisz obliczenia.
Szereg geometryczny [4 punkty]
Dany jest nieskończony ciąg geometryczny \((a_n)\), określony dla każdej liczby naturalnej \(n \ge 1\). Suma trzech początkowych wyrazów ciągu \((a_n)\) jest równa \(7\), a suma \(S\) wszystkich wyrazów tego ciągu jest równa \(8\).
Wyznacz wszystkie wartości \(n\), dla których spełniona jest nierówność \[\left|\frac{S-S_n}{S_n}\lt0{,}001\right|\] gdzie \(S_n\) oznacza sumę \(n\) początkowych wyrazów ciągu \((a_n)\).
Zapisz obliczenia.
Zapisz obliczenia.
Określamy kwadraty \(K_1, K_2, K3_,...\) następująco: 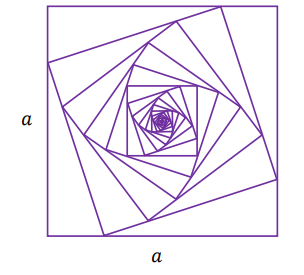
- \(K_1\) jest kwadratem o boku długości \(a\)
- \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1 ∶ 3\)
- \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1 ∶ 3\)
- \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_{n-1}\) i dzieli ten bok w stosunku \(1 ∶ 3\).

Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.
Dany jest nieskończony szereg geometryczny \[2x-\frac{6x}{x-1}+\frac{18x}{(x-1)^2}-\frac{54x}{(x-1)^3}+\ ...\]
Wyznacz wszystkie wartości zmiennej \(x\) (różnej od \(0\) i od \(1\)), dla których suma tego szeregu istnieje i jest równa \(\frac{15}{2}\). Zapisz obliczenia.
Geometria płaska [3-4 punkty]
Dany jest trójkąt \(A B C\), który nie jest równoramienny. W tym trójkącie miara kąta \(ABC\) jest dwa razy większa od miary kąta \(BAC\).
Wykaż, że długości boków tego trójkąta spełniają warunek
\[ |A C|^{2}=|B C|^{2}+|A B| \cdot|B C| \]Dany jest trapez prostokątny \(A B C D\) o kątach prostych przy wierzchołkach \(A\) i \(D\). Ramię \(B C\) trapezu ma długość \(5\) . W ten trapez wpisano okrąg o środku w punkcie \(S\) i promieniu \(2\). Punkt \(P\) jest punktem styczności tego okręgu i dłuższej podstawy \(A B\) tego trapezu (zobacz rysunek). 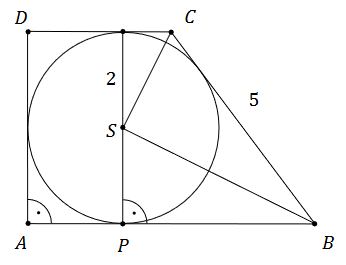
Wykaż, że trójkąty BPS i BSC są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa. Zapisz obliczenia.

W trójkącie ostrokątnym \(ABC\) miara kąta \(BAC\) jest dwa razy większa od miary kąta \(ABC\). Punkt \(D\) jest środkiem boku \(AB\). Niech \(\alpha\) oznacza miarę kąta \(ABC\), natomiast \(\beta\)-miarę kąta \(ADC\) (zobacz rysunek). 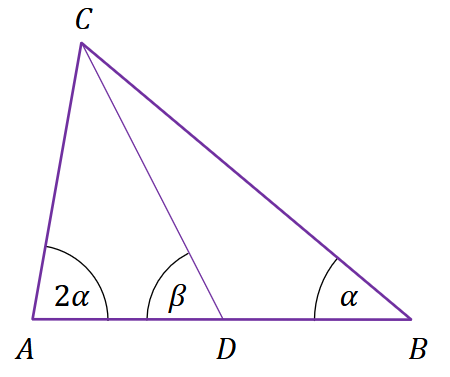

Oblicz \(\frac{\operatorname{tg} \beta}{\sin (2 \alpha)}\). Zapisz obliczenia.
Geometria analityczna [4-5 punktów]
W kartezjańskim układzie współrzędnych \((x, y)\) dane są:
okrąg o równaniu \((x+1)^{2}+(y-3)^{2}=50\) i punkty \(A=(6,4)\) oraz \(B=(-6,8)\).
Punkt \(C\) leży na tym okręgu i \(|A C|=|B C|\).
okrąg o równaniu \((x+1)^{2}+(y-3)^{2}=50\) i punkty \(A=(6,4)\) oraz \(B=(-6,8)\).
Punkt \(C\) leży na tym okręgu i \(|A C|=|B C|\).
Oblicz współrzędne punktu \(C\). Rozważ wszystkie przypadki. Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) środek \(S\) okręgu o promieniu \(\sqrt{5}\) leży na prostej o równaniu \(y=x+1\). Przez punkt \(A=(1,2)\), którego odległość od punktu \(S\) jest większa od \(\sqrt{5}\), poprowadzono dwie proste styczne do tego okręgu w punktach - odpowiednio - \(B\) i \(C\). Pole czworokąta \(ABSC\) jest równe \(15\).
Oblicz współrzędne punktu \(S\). Rozważ wszystkie przypadki. Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) proste o równaniach \(2 x+y-4 m-4=0\) oraz \(x-3 y+5 m+5=0\) przecinają się w punkcie \(P\) o współrzędnych \(\left(x_{P}, y_{P}\right)\).
Wyznacz wszystkie wartości parametru \(m\), dla których współrzędne punktu \(P\) spełniają warunki: \[ x_{P}>0, y_{P}>0, y_{P} \geq x_{P}^{2} \quad \text { oraz } \quad 2<-\frac{8}{\left(y_{P}\right)^{2}}+\frac{8}{x_{P}} \] Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) czworokąt \(A B C D\) jest równoległobokiem takim, że \(\overrightarrow{B D}=[-21,-7]\) i \(\overrightarrow{D C}=[15,8]\).
Oblicz pole tego równoległoboku. Zapisz obliczenia.
Geometria przestrzenna [3-5 punktów]
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(a\). Punkt \(P\) jest środkiem krawędzi \(C G\) tego sześcianu (zobacz rysunek poniżej).  \[ |P G|=|P C| \]
\[ |P G|=|P C| \]
 \[ |P G|=|P C| \]
\[ |P G|=|P C| \] Oblicz odległość wierzchołka \(C\) od płaszczyzny zawierającej punkty \(B, D\) oraz \(P\). Zapisz obliczenia.
W ostrosłupie prawidłowym czworokątnym \(A B C D E\) punkt \(O\) jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy \(A B C D\) do sumy długości wszystkich krawędzi ostrosłupa jest równy \(1: 5\). Przez przekątną \(A C\) podstawy i środek \(S\) krawędzi bocznej \(B E\) poprowadzono płaszczyznę.
Skorzystaj z tablicy wartości funkcji trygonometrycznych (Wybrane wzory matematyczne, strona 34).
Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miare kąta BSO (w zaokrągleniu do \(1^{\circ}\) ). Zapisz obliczenia.
Wskazówka.Skorzystaj z tablicy wartości funkcji trygonometrycznych (Wybrane wzory matematyczne, strona 34).
Iloczyn długości średnicy podstawy walca i wysokości walca jest równy \(12 \sqrt{3}\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).
Oblicz objętość tego walca. Zapisz obliczenia.
Kombinatoryka [3-4 punkty]
Rozważamy wszystkie liczby naturalne, w których zapisie dziesiętnym nie powtarza się jakakolwiek cyfra oraz dokładnie trzy cyfry są nieparzyste i dokładnie dwie cyfry są parzyste.
Oblicz, ile jest wszystkich takich liczb. Zapisz obliczenia.
Niech \(n\) będzie ustaloną liczbą naturalną dodatnią. Ze zbioru \(\mathbb{M}=\{1 ; 2 ; 3 ; \ldots ; 3 n+1\}\) losujemy jednocześnie trzy liczby. Zdarzenie \(A\) odpowiada jednoczesnemu wylosowaniu ze zbioru \(\mathbb{M}\) trzech liczb, których suma przy dzieleniu przez \(3\) daje resztę \(1\).
Oblicz prawdopodobieństwo zdarzenia \(\boldsymbol{A}\). Zapisz obliczenia.
Wzór Bayesa i schemat Bernoulliego [3-4 punkty]
Tutaj może również pojawić się zadanie na zwykłe prawdopodobieństwo warunkowe, ale obstawiam większą szansę na Bayesa lub Bernoulliego.Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe \(0{,}1\).
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych. Zapisz obliczenia.
Egzamin składa się z \(15\) zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej \(11\) zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny.
Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
Zapisz obliczenia.
Pewna choroba dotyka \(0,2 \%\) całej populacji i w początkowym stadium nie daje widocznych objawów chorobowych. W ramach profilaktyki stosuje się pewien test przesiewowy, który daje wynik pozytywny lub negatywny. Prawdopodobieństwo tego, że test wykonany na osobie chorej da wynik pozytywny (oznaczający chorobę), jest równe \(0,99\). Ponadto wiadomo, że prawdopodobieństwo tego, że test wykonany na osobie zdrowej da wynik negatywny, jest równe \(0,98\).
Pan X poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby.
Pan X poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby.
Oblicz prawdopodobieństwo tego, że pan X jest rzeczywiście chory. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych. Zapisz obliczenia.
W pewnej lokalnej społeczności \(35 \%\) osób ma wyższe wykształcenie. W tej społeczności językiem niemieckim dobrze włada \(70 \%\) osób mających wyższe wykształcenie i \(40 \%\) osób bez wyższego wykształcenia.
Spośród członków tej społeczności wybieramy losowo jedną osobę.
Spośród członków tej społeczności wybieramy losowo jedną osobę.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wybierzemy osobę z wyższym wykształceniem, jeżeli wiadomo, że ta osoba dobrze włada językiem niemieckim. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych. Zapisz obliczenia.
Granice [2-3 punkty]
Oblicz granicę \[ \lim _{x \rightarrow 2^{-}} \frac{x^{3}-8}{(x-2)^{2}} \] Zapisz obliczenia.
Oblicz granicę \[ \lim _{x \rightarrow 3^{-}} \frac{|x-3|}{x^{2}-9} \] Zapisz obliczenia.
Oblicz granice \(\lim _{n \rightarrow \infty} \sqrt[n]{6^{n}+7^{n}}\). Zapisz obliczenia.
Oblicz granicę \[ \lim _{n \rightarrow+\infty} \frac{1+3+5+7+\ldots+(2 n+1)}{\binom{n}{2}} \] gdzie \(1+3+5+7+\ldots+(2 n+1)\) jest sumą kolejnych liczb naturalnych nieparzystych.
Własność Darboux [3 punkty]
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2 x-3}{x+2}+4 \log _{\frac{1}{2}} x\) dla każdego \(x\gt 0\).
Wykaż, że funkcja \(\boldsymbol{f}\) ma co najmniej jedno miejsce zerowe, które należy do przedziału \(\left[\frac{1}{2}, 4\right]\).
Funkcja \(f\) jest określona wzorem \(f(x)=x^{6}-2 x^{4}-x^{3}+1\) dla każdego \(x \in \mathbb{R}\).
Wykaż, że liczba \(5\) należy do zbioru wartości tej funkcji.
Pochodna i styczna do wykresu funkcji [3 punkty]
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2+3}{x-1}\) dla każdej liczby rzeczywistej \(x \ne 1\).
Wyznacz równanie stycznej do wykresu tej funkcji w punkcie \(P=(-3,-3)\).
Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x) = \frac{3x^2-2x}{x^2+2x+8}\) dla każdej liczby rzeczywistej \(x\). Punkt \(P = (x_0, 3)\) należy do wykresu funkcji \(f\).
Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x) = 2x^3-4x^2+9x\) dla każdego \(x\in \mathbb{R} \). Punkt \(P = (x_0, 18)\) należy do wykresu funkcji \(f\).
Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Monotoniczności i ekstrem funkcji [3 punkty]
Wykaż, że dla każdej liczby rzeczywistej dodatniej \(a\) prawdziwa jest nierówność \[a^2+\frac{16}{a}\ge12\]
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{3x}{x+1}\) dla każdego \(x \in(-1,+\infty)\).
Wykaż, że \(f\) jest funkcją rosnącą.
Funkcja wymierna \(f\) jest dana wzorem \(f(x)=\frac{x+1}{x^2+2x+2}\). Wyznacz wartość najmniejszą i wartość największą, jakie ta funkcja przyjmuje dla argumentów z przedziału \(\langle -3,1 \rangle \)
Funkcja \(f\) jest określona wzorem \(f(x)=x^{4}+0,5 \cdot(2 x+1)^{4}\) dla każdego \(x \in \mathbb{R}\).
Oblicz najmniejszą wartość tej funkcji. Zapisz obliczenia.
Inne zagadnienia
- układy równań z parametrem
- wielomiany (pierwiastki wymierne)
- równania z wartościami bezwzględnymi
Dany jest układ równań \[ \left\{\begin{array}{l} m x+y=m^{2} \tag{1}\\ 4 x+m y=8 \end{array}\right. \] z niewiadomymi \(x\) i \(y\) oraz parametrem \(m \in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(m\), dla których układ jest oznaczony, a para liczb \((x, y)\) będąca rozwiązaniem układu spełnia warunek \(|x+y|\lt2\). Zapisz obliczenia.
Wielomian \(W\) jest określony wzorem \(W(x)=(x-1)\left(x^{2}-m x+m-1\right)\) dla każdego \(x \in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(\boldsymbol{m}\), dla których wielomian \(\boldsymbol{W}\) ma dokładnie jeden pierwiastek rzeczywisty. Zapisz obliczenia.
Rozwiąż równanie \[ |4x-8|+|x-2|=|2-x|+|x+2|+4 \]
Tematy nadrzędne i sąsiednie

