Pewniaki do matury podstawowej 2026
Poziom podstawowy
Pewniaki do matury 2026!
Strona zawiera wszystkie typy zadań, które mają największą szansę pojawić się na maturze podstawowej w nowej formule w roku 2026.
Wybrane typy zadań stanowią ok 75% punktów do zdobycia na maturze.
Strona zawiera wszystkie typy zadań, które mają największą szansę pojawić się na maturze podstawowej w nowej formule w roku 2026.
Wybrane typy zadań stanowią ok 75% punktów do zdobycia na maturze.
Jak wybrałem pewniaki?
Pewniaki to są typy zadań, które pojawiały się najczęściej we wszystkich ostatnich oficjalnych arkuszach i materiałach od CKE i są zgodne z najnowszymi wymaganiami.
Pewniaki to są typy zadań, które pojawiały się najczęściej we wszystkich ostatnich oficjalnych arkuszach i materiałach od CKE i są zgodne z najnowszymi wymaganiami.
Pełną wiedzę niezbędną do zdania matury na 100% znajdziesz w KURSIE do nowej matury podstawowej.
Spis zagadnień
Wytłuszczonym drukiem zaznaczyłem te zagadnienia, które minimalnym wysiłkiem pozwalają zdobyć dużo punktów. Zagadnienia z * już nie zaliczają się do "pewniaków" i szansa na ich pojawienie się wynosi ok 50%.
Potęgi i pierwiastki [1 punkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(3^{-2,4}\cdot 3^{\Large{\frac{2}{5}}}\right)^{\Large{\frac{1}{2}}}\) jest równa A.\( \sqrt{3} \)
B.\( \frac{\sqrt{3}}{3} \)
C.\( \frac{1}{3} \)
D.\( 0{,}3 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sqrt[3]{-\frac{27}{16}}\cdot \sqrt[3]{2}\) jest równa A.\( \left(-\frac{3}{2}\right) \)
B.\( \frac{3}{2} \)
C.\( \frac{2}{3} \)
D.\( \left(-\frac{2}{3}\right) \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\sqrt[5]{5} \cdot \frac{1}{5}\right)^{-5}\) jest równa A.\(5^{4}\)
B.\(5^{-4}\)
C.\(5^{0,25}\)
D.\(5^{-0,25}\)
Liczba \(\log_2\left[(\sqrt{2})^2\cdot (\sqrt{2})^4\cdot (\sqrt{2})^8\right]\) jest równa
A.\( \sqrt{2} \)
B.\( 7 \)
C.\( 14 \)
D.\( 2^7 \)
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(\frac{\sqrt[3]{250}+\sqrt[3]{54}}{\sqrt[3]{250}-\sqrt[3]{54}}\) jest równa A.\(\sqrt[3]{\frac{76}{49}}\)
B.\( (-1) \)
C.\( 4 \)
D.\( 4 \sqrt[3]{2} \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej \(x\) iloczyn \(\sqrt{x}\cdot \sqrt[3]{x}\cdot \sqrt[6]{x}\) jest równy A.\( x \)
B.\( \sqrt[10]{x} \)
C.\( \sqrt[18]{x} \)
D.\( x^2 \)
Logarytmy [1 punkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_2\frac{1}{8} + \log_2 4\) jest równa A.\( (-1) \)
B.\( \frac{1}{2} \)
C.\( 2 \)
D.\( 5 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log_{25}1-\frac{1}{2}\log_{25}5\) jest równa A.\( \left(-\frac{1}{4}\right) \)
B.\( \left(-\frac{1}{2}\right) \)
C.\( \frac{1}{4} \)
D.\( \frac{1}{2} \)
Dane są liczby \(a=\log _2(3 \sqrt{5}+\sqrt{13})\) oraz \(b=\log _2(3 \sqrt{5}-\sqrt{13})\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(a+b\) jest równa A.\(\log _2 45\)
B.\(\log _2 30\)
C.\(4\)
D.\(5\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej \(x\) i dla każdej dodatniej liczby rzeczywistej \(y\) wartość wyrażenia \(\log _{7} x+6 \log _{7} y\) jest równa wartości wyrażenia A.\(\log _{7}\left(\frac{x}{y^{6}}\right)\)
B.\(\log _{7}(x y)^{6}\)
C.\(\log _{7}(6 x y)\)
D.\(\log _{7}\left(x y^{6}\right)\)
Wartość bezwzględna [1 punkt]
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Liczba \(|\sqrt{5}-1|-3|2-\sqrt{5}|\) jest równa A.\((-7)\)
B.\(5-4 \sqrt{5}\)
C.\(4 \sqrt{5}-7\)
D.\(5-2 \sqrt{5}\)
Liczby \(x_{1}\) i \(x_{2}\) są różnymi rozwiązaniami równania \(|x+4|=7\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma \(x_{1}+x_{2}\) jest równa A.\((-14)\)
B.\((-8)\)
C.\(3\)
D.\(8\)
Wartość wyrażenia \( \vert{3-x}\vert-\vert{x+4}\vert \) dla \( x \in (3,+\infty) \) jest równa
A.\(7-2x \)
B.\(-2x-1 \)
C.\(7 \)
D.\(-7 \)
Dla każdej liczby \( x \), spełniającej warunek \( -3 \lt x \lt 0 \), wyrażenie \( \frac{|x+3|-x+3}{x} \) jest równe
A.\(2 \)
B.\(3 \)
C.\(-\frac{6}{x} \)
D.\(\frac{6}{x} \)
Zadania dowodowe z podzielnością i resztą [2-3 punkty]
Udowodnij, że dla każdej liczby całkowitej \(n\) liczba \((3 n+5)^2+11 n^2-18\) przy dzieleniu przez \(5\) daje resztę \(2\).
Wykaż, że dla każdej liczby naturalnej \(n \geq 1\) liczba \(n\left(n^2+3 n+2\right)\) jest podzielna przez \(6\).
Wykaż, że dla każdej liczby całkowitej nieparzystej \(n\) liczba \(3n^2+4n+1\) jest podzielna przez \(4\).
Udowodnij, że liczba \(3^{45}+9^{22}+27^{14}\) jest podzielna przez \(37\).
Wykaż, że liczba \(2^{100}+4^{49}+16^{24}\) jest podzielna przez \(21\).
Rozważmy dwie kolejne liczby naturalne \(a\) i \(b\) takie, że \(a\lt b\) oraz obie są niepodzielne przez \(3\).
Udowodnij, że liczba \(a^2+11 a b+b^2\) jest podzielna przez \(9\).
Wyrażenia wymierne [1 punkt]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(\frac{(x^2-3x)(x+2)}{x^2-4}=0\) w zbiorze liczb rzeczywistych ma dokładnie A.jedno rozwiązanie.
B.dwa rozwiązania.
C.trzy rozwiązania.
D.cztery rozwiązania.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) różnej od \(0\) i \(2\) wyrażenie \(\frac{x^2+x}{(x-2)^2}\cdot \frac{x-2}{x}\) jest równe A.\( \frac{x^2+1}{x-2} \)
B.\( \frac{x+1}{2} \)
C.\( \frac{x^2}{(x-2)^2} \)
D.\( \frac{x+1}{x-2} \)
Równania wymierne [3 punkty]
Dane jest równanie \[ \frac{2}{2 x+1}=\frac{x-1}{x+2} \]
Wyznacz dziedzinę tego równania. Rozwiąż to równanie.
Rozwiąż równanie \[\frac{x+3}{x-1}=\frac{x}{2 x-2}\] Zapisz konieczne założenie i obliczenia.
Nierówności kwadratowe [2 punkty]
Rozwiąż nierówność
\[(3 x-4)(x-1)\lt x\]Rozwiąż nierówność \[ x(x-6) \leq 7 \] Zapisz obliczenia.
Analiza wykresu funkcji [4 punkty]
W kartezjańskim układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dziedziną funkcji \(f\) jest zbiór
A.\( [-6,5] \)
B.\( (-6,5) \)
C.\( (-3,5] \)
D.\( [-3,5] \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największa wartość funkcji \(f\) w przedziale \([−4, 1]\) jest równa A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( 5 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest malejąca w zbiorze A.\( [-6,-3) \)
B.\( [-3,1] \)
C.\( (1,2] \)
D.\( [2,5] \)
W kartezjańskim układzie współrzędnych \((x, y)\) narysowano wykres funkcji \(y = f(x)\) (zobacz rysunek). 

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-F.
| Dziedziną funkcji \(f\) jest zbiór | |
| Zbiorem wartości funkcji \(f\) jest zbiór |
A.\( [-3,-1]\cup [1,3] \)
B.\( (-3,3) \)
C.\( (-3,-1)\cup (1,3) \)
D.\( [-5,-1]\cup [1,5] \)
E.\( (-5,5) \)
F.\( (-5,-1)\cup (1,5) \)
Zapisz poniżej zbiór wszystkich rozwiązań nierówności \(f(x)\lt -1\).
.......................................................
W kartezjańskim układzie współrzędnych \((x, y)\) narysowano wykres funkcji \(y = f(x)\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest rosnąca w przedziale A.\( [-5,4] \)
B.\( [5,7] \)
C.\( [1,5] \)
D.\( [-1,5] \)
Zapisz poniżej w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości większe od \(1\).
....................................................................
Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x) = f(-x)\) dla każdego \(x\in [-7,-5]\cup [-4,4]\cup [5,7]\). Na jednym z rysunków A-D przedstawiono, w kartezjańskim układzie współrzędnych \((x, y)\), wykres funkcji \(y = g(x)\). 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wykres funkcji \(y = g(x)\) przedstawiono na rysunku 
W kartezjańskim układzie współrzędnych \((x, y)\) przedstawiono fragment wykresu funkcji kwadratowej \(f\) (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji \(f\), oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wartości funkcji \(f\) jest przedział A.\( (-\infty,-2\rangle \)
B.\( (-\infty,4\rangle \)
C.\( \langle -2,+\infty) \)
D.\( \langle 4,+\infty) \)
Zapisz poniżej w postaci przedziału zbiór wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości ujemne.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Wzór funkcji \(f\) można przedstawić w postaci: ………. oraz ………. . A.\( f(x)=\frac{1}{2}(x-2)(x-6) \)
B.\( f(x)=\frac{1}{2}(x-4)^2-2 \)
C.\( f(x)=2(x-2)(x-6) \)
D.\( f(x)=\frac{1}{2}(x+4)^2-2 \)
E.\( f(x)=2(x+2)(x+6) \)
F.\( f(x)=2(x+4)^2-2 \)
Funkcja kwadratowa \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x) = f(x + 1)\). Na jednym z rysunków A-D przedstawiono, w kartezjańskim układzie współrzędnych \((x, y)\), fragment wykresu funkcji \(y = g(x)\). 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Fragment wykresu funkcji \(y = g(x)\) przedstawiono na rysunku 
Funkcja liniowa i proste równoległe[1-2 punkt]
W kartezjańskim układzie współrzędnych \((x, y)\) dane są proste \(k\) oraz \(l\) o równaniach \[k: y=-\frac{1}{2}x-7\] \[l: y=(2m-1)x+13\]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Proste \(k\) oraz \(l\) są równoległe, gdy A.\( m=-\frac{1}{2} \)
B.\( m=\frac{1}{4} \)
C.\( m=\frac{3}{2} \)
D.\( m=2 \)
Na rysunku, w kartezjańskim układzie współrzędnych \((x, y)\), przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego \(z\) poniższych układów równań A-D. 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest A.\(\left\{\begin{array}{l}y=-\frac{3}{2} x+3 \\ y=-\frac{3}{2} x-1\end{array}\right.\)
B.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=-\frac{2}{3} x-1\end{array}\right.\)
C.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=\frac{3}{2} x-1\end{array}\right.\)
D.\(\left\{\begin{array}{l}y=-\frac{3}{2} x-3 \\ y=\frac{3}{2} x+1\end{array}\right.\)
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
W kartezjańskim układzie współrzędnych \((x, y)\) wykresy funkcji liniowych \(f(x)=(2m+7) x+5\) oraz \(g(x)=3x\) nie maja punktów wspólnych dla A.\(m=-2\)
B.\(m=-1\)
C.\(m=1\)
D.\(m=2\)
Miejscem zerowym funkcji liniowej \(f\) jest liczba 2, a punkt przecięcia wykresu funkcji \(f\) z osią \(O y\) kartezjańskiego układu współrzędnych \((x, y)\) ma współrzędne \((0,4)\) (zobacz rysunek). 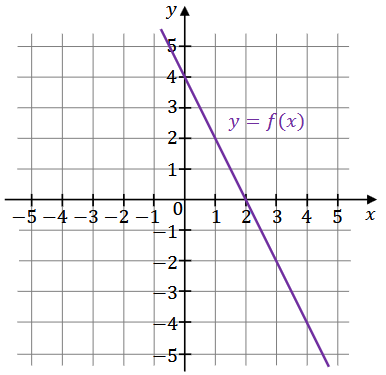
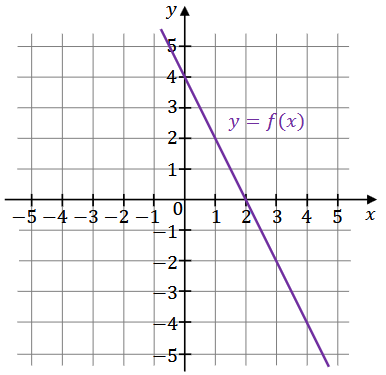
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Współczynnik kierunkowy prostej, która jest wykresem funkcji \(f\), jest równy \((-2)\). | P | F |
| Pole trójkąta ograniczonego osiami kartezjańskiego układu współrzędnych \((x, y)\) oraz wykresem funkcji \(f\) jest równe \(8\). | P | F |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dany jest trapez \(A B C D\), w którym boki \(AB\) i \(CD\) są równoległe oraz \(C=(3,15)\). Wierzchołki \(A\) i \(B\) tego trapezu leżą na prostej o równaniu \(3x-y+10=0\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Bok \(CD\) tego trapezu zawiera się w prostej o równaniu A.\(y=3 x+15\)
B.\(y=3 x+6\)
C.\(y=\frac{5}{3} x+10\)
D.\(y=-\frac{1}{3} x+16\)
Kąty w okręgu [1 punkt]
Punkty \(A, B, C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę \(70^\circ\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta ostrego \(ABC\) jest równa A.\( 10^\circ \)
B.\( 20^\circ \)
C.\( 35^\circ \)
D.\( 40^\circ \)
Na łukach \(AB\) i \(CD\) okręgu są oparte kąty wpisane \(ADB\) i \(DBC\), takie, że \(|\sphericalangle ADB| = 20^\circ\) i \(|\sphericalangle DBC| = 40^\circ\) (zobacz rysunek). Cięciwy \(AC\) i \(BD\) przecinają się w punkcie \(K\). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta \(DKC\) jest równa A.\( 80^\circ \)
B.\( 60^\circ \)
C.\( 50^\circ \)
D.\( 40^\circ \)
W okręgu \(O\) kąt środkowy \(\beta\) oraz kąt wpisany \(\alpha\) są oparte na tym samym łuku. Kąt \(\beta\) ma miarę o \(40^\circ\) większą od kąta \(\alpha\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta \(\beta\) jest równa A.\( 40^\circ \)
B.\( 80^\circ \)
C.\( 100^\circ \)
D.\( 120^\circ \)
Punkty \(A\), \(B\) oraz \(C\) leżą na okręgu o środku w punkcie \(O\). Prosta \(k\) jest styczna do tego okręgu w punkcie \(A\) i tworzy z cięciwą \(AB\) kąt o mierze \(32^\circ\). Ponadto odcinek \(AC\) jest średnicą tego okręgu (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta rozwartego \(BOC\) jest równa A.\( 148^\circ \)
B.\( 116^\circ \)
C.\( 154^\circ \)
D.\( 122^\circ \)
Ciąg geometryczny i arytmetyczny [2 punkt]
Trzywyrazowy ciąg \((27, 9, a - 1)\) jest geometryczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa A.\( 3 \)
B.\( 0 \)
C.\( 4 \)
D.\( 2 \)
Trzywyrazowy ciąg \((1, 4, a + 5)\) jest arytmetyczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa A.\( 0 \)
B.\( 7 \)
C.\( 2 \)
D.\( 11 \)
Ciąg \((3x^2+5x,x^2,20-x^2)\) jest arytmetyczny.
Oblicz \(x\). Zapisz obliczenia.
Trzywyrazowy ciąg \((1 - 2a, 12, 48)\) jest geometryczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa A.\( (-1) \)
B.\( 3 \)
C.\( 4 \)
D.\( 12{,}5 \)
Dany jest ciąg geometryczny \(\left(a_{n}\right)\) określony dla każdej liczby naturalnej \(n \geq 1\), w którym \(a_{2}=\frac{1}{6}\) oraz \(a_{3}=\frac{1}{9}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Piąty wyraz ciągu \(\left(a_{n}\right)\) jest równy A.\(\frac{1}{15}\)
B.\(\frac{2}{27}\)
C.\(\frac{4}{81}\)
D.\(\frac{8}{243}\)
Ciąg określony ogólnie [1 punkt]
Ciąg \((a_n)\) jest określony wzorem \(a_n = 2^n \cdot (n + 1)\) dla każdej liczby naturalnej \(n \ge 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wyraz \(a_4\) jest równy A.\( 64 \)
B.\( 40 \)
C.\( 48 \)
D.\( 80 \)
Ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{n-2}{3}\) dla każdej liczby naturalnej \(n \ge 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba wyrazów tego ciągu mniejszych od \(10\) jest równa A.\( 28 \)
B.\( 31 \)
C.\( 32 \)
D.\( 27 \)
Ciąg \((a_n)\) jest określony wzorem \(a_n=(-1)^n\cdot \frac{n+1}{2}\) dla każdej liczby naturalnej \(n \ge 1\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Trzeci wyraz tego ciągu jest równy A.\( 2 \)
B.\( (-2) \)
C.\( 3 \)
D.\( (-1) \)
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n \ge 1\). Suma \(n\) początkowych wyrazów tego ciągu jest określona wzorem \(S_n = 4\cdot (2^n - 1)\) dla każdej liczby naturalnej \(n \ge 1\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.
| Pierwszy wyraz ciągu \((a_n)\) jest równy \(4\). | P | F |
| Drugi wyraz ciągu \((a_n)\) jest równy \(12\). | P | F |
Obliczanie funkcji trygonometrycznych [1 punkt]
W kartezjańskim układzie współrzędnych \((x, y)\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O = (0, 0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(Ox\), a drugie przechodzi przez punkt \(P = (-3, 1)\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta \(\alpha\) jest równy A.\( \frac{1}{\sqrt{10}} \)
B.\( \left(-\frac{3}{\sqrt{10}}\right) \)
C.\( \left(-\frac{3}{1}\right) \)
D.\( \left(-\frac{1}{3}\right) \)
Kąt \(\alpha\) jest ostry i \(\cos \alpha = \frac{2\sqrt{6}}{7}\) .
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Sinus kąta \(\alpha\) jest równy A.\( \frac{24}{49} \)
B.\( \frac{5}{7} \)
C.\( \frac{25}{49} \)
D.\( \frac{\sqrt{6}}{7} \)
Kąt o mierze \(\alpha\) jest rozwarty oraz \(\sin \alpha=\frac{\sqrt{3}}{4}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cosinus kąta o mierze \(\alpha\) jest równy A.\(\left(-\frac{\sqrt{13}}{4}\right)\)
B.\(\left(-\frac{1}{2}\right)\)
C.\(\frac{1}{2}\)
D.\(\frac{\sqrt{13}}{4}\)
Dane są dwa kąty o miarach \(\alpha\) oraz \(\beta\), spełniające warunki:

\(\alpha \in (0^\circ, 180^\circ)\) i \(\operatorname{tg} \alpha = -\frac{2}{3}\) oraz \(\beta \in (0^\circ, 180^\circ)\) i \(\cos \beta = \frac{1}{\sqrt{10}}\).
Na rysunkach A-F w kartezjańskim układzie współrzędnych \((x, y)\) zaznaczono różne kąty - w tym kąt o mierze \(\alpha\) oraz kąt o mierze \(\beta\). Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią \(Ox\), a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: \(A\) lub \(B\), lub \(C\), lub \(D\), lub \(E\), lub \(F\).
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-F.
| 1. | Kąt \(\alpha\) jest zaznaczony na rysunku | |
| 2. | Kąt \(\beta\) jest zaznaczony na rysunku |

Równanie okręgu [1 punkt]
Na płaszczyźnie, w kartezjańskim układzie współrzędnych \((x, y)\), dany jest okrąg \(\mathcal{O}\) określony równaniem: \[ (x-2)^2+(y+3)^2=16 \] 2. Promień \(r\) okręgu \(\mathcal{O}\) jest równy
Dokończ zdania. Zaznacz odpowiedź spośród A-D oraz odpowiedź spośród E-G.
1. Ṡrodek \(S\) okręgu \(\mathcal{O}\) ma współrzędne A.\(S=(2,-3)\)
B.\(S=(-2,-3)\)
C.\(S=(-2,3)\)
D.\(S=(-2,3)\)
E.\(r=16\)
F.\(r=4\)
G.\(r=5\)
W kartezjańskim układzie współrzędnych \((x, y)\) dane są cztery okręgi: \(o_{1}, o_{2}, o_{3}, o_{4}\), o równaniach: \[ \begin{aligned} & o_{1}:(x-1)^{2}+(y-2)^{2}=1 \\[6pt] & o_{2}:(x+1)^{2}+(y+2)^{2}=9 \\[6pt] & o_{3}:(x-3)^{2}+(y-4)^{2}=4 \\[6pt] & o_{4}:(x+3)^{2}+(y+4)^{2}=16 \end{aligned} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okręgiem, który nie ma żadnego punktu wspólnego z osiami układu współrzędnych \((x, y)\), jest A.\(o_{1}\)
B.\(o_{2}\)
C.\(o_{3}\)
D.\(o_{4}\)
Bryły obrotowe [1-2 punkty]
Pole powierzchni bocznej walca jest równe \(16 \pi\), a promień jego podstawy ma długość \(2\).
Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Objętość tego walca jest równa A.\( 16 \)
B.\( 32 \)
C.\( 16 \pi \)
D.\( 32 \pi \)
Objętość stożka o wysokości \(2\) jest równa \(8 \pi\).
Oblicz miarę kąta rozwarcia tego stożka. Zapisz obliczenia.
Kombinatoryka - reguła mnożenia[1-2 punkty]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry \(0, 5, 7\) (np. \(57\ 075, 55\ 555\)), jest A.\( 5^3 \)
B.\( 2\cdot 4^3 \)
C.\( 2\cdot 3^4 \)
D.\( 3^5 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym cyfry się nie powtarzają, jest A.\( 9\cdot 10\cdot 10\cdot 10\cdot 10 \)
B.\( 9\cdot 9\cdot 9\cdot 9\)
C.\( 10\cdot 9\cdot 8\cdot 7\)
D.\( 9\cdot 9\cdot 8\cdot 7\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych trzycyfrowych o sumie cyfr równej \(3\) jest A.\( 8 \)
B.\( 4 \)
C.\( 5 \)
D.\( 6 \)
E-dowód ma zapisany na pierwszej stronie specjalny sześciocyfrowy numer CAN, który zabezpiecza go przed odczytaniem danych przez osoby nieuprawnione.
Oblicz, ile jest wszystkich sześciocyfrowych numerów CAN o różnych cyfrach, spełniających warunek: trzy pierwsze cyfry są kolejnymi wyrazami ciągu arytmetycznego o różnicy \((-3)\). Zapisz obliczenia.
Prawdopodobieństwo klasyczne [1-2 punkty]
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek - od jednego oczka do sześciu oczek.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe A.\( \frac{1}{2} \)
B.\( \frac{1}{5} \)
C.\( \frac{1}{4} \)
D.\( \frac{3}{4} \)
Ze zbioru ośmiu liczb \(\{2, 3, 4, 5, 6, 7, 8, 9\}\) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez \(15\). Zapisz obliczenia.
Ze zbioru ośmiu kolejnych liczb naturalnych - od \(1\) do \(8\) - losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech \(A\) oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby \(8\).
Oblicz prawdopodobieństwo zdarzenia \(A\). Zapisz obliczenia.
Ze zbioru pięciu liczb \(\{1, 2, 3, 4, 5\}\) losujemy bez zwracania kolejno dwa razy po jednej liczbie.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że obie wylosowane liczby są nieparzyste. Zapisz obliczenia
Dane są dwa zbiory: \(C=\{1,2,3,4,5,6\}\) oraz \(D=\{7,8,9,10\}\). Losujemy jedną liczbę ze zbioru \(C\), a następnie losujemy jedną liczbę ze zbioru \(D\).
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że wylosujemy liczby, których iloczyn będzie podzielny przez \(4\). Zapisz obliczenia.
Średnia arytmetyczna, mediana, dominanta [1-2 punkty]
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach. 

Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
| 1. | Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa | |
| 2. | Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa |
A.\( 5{,}80 \)
B.\( 5{,}73 \)
C.\( 5{,}85 \)
D.\( 6{,}00 \)
E.\( 5{,}70 \)
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku. 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa A.\( 5\ 690 \) zł
B.\( 5\ 280\) zł
C.\( 6\ 257\) zł
D.\( 5\ 900\) zł
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [\(19\) dag, \(21\) dag]. Pobrano próbę kontrolną liczącą \(50\) jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano - wyrażoną w dekagramach - masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie. 

Spośród \(50\) zważonych jabłek z pobranej próby kontrolnej losujemy jedno jabłko.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowane jabłko spełnia normę jakości, jest równe A.\( \frac{3}{7} \)
B.\( \frac{5}{7} \)
C.\( \frac{18}{25} \)
D.\( \frac{9}{10} \)
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.
Dominanta masy \(50\) zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa | A. | 20 dag | ponieważ | 1. | ta masa jest największa w tej próbie. |
| 2. | iloczyn tej masy i liczby jabłek o takiej masie jest największy w tej próbie. | |||
| B. | 23 dag | |||
| 3. | ta masa występuje najliczniej w tej próbie. | |||
Zadanie optymalizacyjne [4 punkty]
Działka ma kształt trapezu. Podstawy \(AB\) i \(CD\) tego trapezu mają długości \(|AB| = 400\) m oraz \(|CD| = 100\) m. Wysokość trapezu jest równa \(75\) m, a jego kąty \(DAB\) i \(ABC\) są ostre.
Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie \(AB\) tego trapezu, a dwa pozostałe - \(E\) oraz \(F\) - na ramionach \(AD\) i \(BC\) trapezu (zobacz rysunek).
Aby powiązać ze sobą wymiary prostokąta, skorzystaj z tego, że pole trapezu \(ABCD\) jest sumą pól trapezów \(ABFE\) oraz \(EFCD\): \[P_{ABCD}=P_{ABFE}+P_{EFCD}\]
Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie \(AB\) tego trapezu, a dwa pozostałe - \(E\) oraz \(F\) - na ramionach \(AD\) i \(BC\) trapezu (zobacz rysunek).

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię. Zapisz obliczenia.
Wskazówka:Aby powiązać ze sobą wymiary prostokąta, skorzystaj z tego, że pole trapezu \(ABCD\) jest sumą pól trapezów \(ABFE\) oraz \(EFCD\): \[P_{ABCD}=P_{ABFE}+P_{EFCD}\]
Zakład stolarski produkuje krzesła, które sprzedaje po \(196\) złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
- przychód \(P\) (w złotych) ze sprzedaży \(x\) krzeseł można opisać funkcją \(P(x) = 196x\)
- koszt \(K\) (w złotych) produkcji \(x\) krzeseł dziennie można opisać funkcją \[K(x) = 4x^2 + 4x + 240\]
Wskazówka: przyjmij, że zysk jest różnicą przychodu i kosztów.
Zgodnie z założeniem architekta okno na poddaszu ma mieć kształt trapezu równoramiennego, który nie jest równoległobokiem. Dłuższa podstawa trapezu ma mieć długość \(12\) dm, a suma długości krótszej podstawy i wysokości tego trapezu ma być równa \(18\) dm.
Oblicz, jaką długość powinna mieć krótsza podstawa tego trapezu, tak aby pole powierzchni okna było największe. Oblicz to pole. Zapisz obliczenia.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z \(30\) kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja \[L(n) = -n^2 + 22n + 279\] gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n \ge 1\) i \(n \le 30\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. | Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\). | P | F |
| W trzecim dniu analizowanego okresu obsłużono \(336\) klientów. | P | F |
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Podobieństwo figur (trójkątów) [1 punkt]
Trójkąty prostokątne \(T_1\) i \(T_2\) są podobne. Przyprostokątne trójkąta \(T_1\) mają długości 5 i 12. Przeciwprostokątna trójkąta \(T_2\) ma długość \(26\).
Oblicz pole trójkąta \(T_2\). Zapisz obliczenia.
W trapezie \(ABCD\) o podstawach \(AB\) i \(CD\) przekątne przecinają się w punkcie \(E\) (zobacz rysunek). 

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Trójkąt \(ABE\) jest podobny do trójkąta \(CDE\). | P | F |
| Pole trójkąta \(ACD\) jest równe polu trójkąta \(BCD\). | P | F |
Trapez \(T_1\), o polu równym \(52\) i obwodzie \(36\), jest podobny do trapezu \(T_2\). Pole trapezu \(T_2\) jest równe \(13\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód trapezu \(T_2\) jest równy A.\( 18 \)
B.\( 9 \)
C.\( \frac{169}{9} \)
D.\( \frac{52}{3} \)
Dany jest okrąg \(O\) o środku w punkcie \(S\). Średnica \(AB\) tego okręgu przecina cięciwę \(CD\) w punkcie \(P\) (zobacz rysunek). Ponadto: \(|PB| = 4\), \(|PC| = 8\) oraz \(|PD| = 5\). 

Oblicz promień okręgu \(O\). Zapisz obliczenia.
Geometria przestrzenna z zaznaczonym kątem [3-4 punkty]
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\) i ma długość równą \(6\) (zobacz rysunek). 

Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.
Dany jest graniastosłup prawidłowy sześciokątny \(ABCDEFA'B'C'D'E'F'\), w którym krawędź podstawy ma długość \(5\). Przekątna \(AD'\) tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(45^\circ\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole ściany bocznej tego graniastosłupa jest równe A.\( 12{,}5 \)
B.\( 25 \)
C.\( 50 \)
D.\( 100 \)
Objętość ostrosłupa prawidłowego czworokątnego jest równa \(384\). Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze \(\alpha\) taki, że \(\operatorname{tg} \alpha =\frac{4}{3}\) (zobacz rysunek). 

Oblicz wysokość ściany bocznej tego ostrosłupa. Zapisz obliczenia.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą \(6\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni całkowitej tego graniastosłupa jest równe A.\( 216+18\sqrt{3} \)
B.\( 216+54\sqrt{3} \)
C.\( 216+216\sqrt{3} \)
D.\( 216+108\sqrt{3} \)
Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa. Zapisz obliczenia.
Inne ważne zagadnienia
- procent składany i kapitalizacja odsetek
- równania i nierówności liniowe
- układy równań liniowych
- przesunięcia wykresów funkcji
- ciągi rekurencyjne
- funkcja wykładnicza i czas połowicznego rozpadu
- jedynka trygonometryczna
- wzory na pole trójkąta (trójkąt równoboczny)
- twierdzenie Pitagorasa i Talesa
- symetrie osiowe
- własności trójkąta wpisanego i opisanego na okręgu
- długość odcinka w układzie współrzędnych
Tematy nadrzędne i sąsiednie


