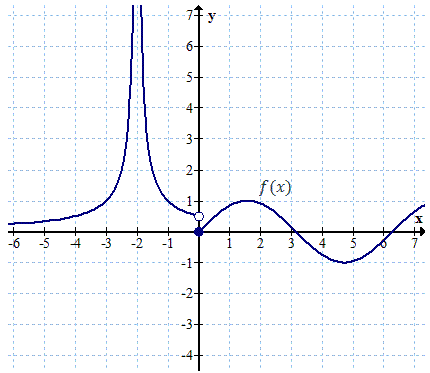
Zacznijmy od naszkicowania wykresu tej funkcji: W punkcie \(x_1 = -2\) funkcja nie jest określona, zatem badamy granicę lewostronną i prawostronną: \[\begin{split} &\lim_{x \to -2^{-}}f(x)=+\infty \\[6pt] &\lim_{x \to -2^{+}}f(x)=+\infty \end{split}\] Obie granice są równe, zatem: \[\lim_{x \to -2}f(x)=+\infty \] W punkcie \(x_2 = 0\) funkcja jest nieciągła, zatem liczymy granicę lewostronną i prawostronną: \[\begin{split} &\lim_{x \to 0^{-}}f(x)=\frac{1}{2} \\[6pt] &\lim_{x \to 0^{+}}f(x)=0 \end{split}\] Granica lewostronna jest różna od prawostronnej zatem granica w punkcie \(x_2\) nie istnieje. W punkcie \(x_3 = \pi\) funkcja jest określona i ciągła, zatem liczymy granicę wprost ze wzoru: \[\lim_{x \to \pi }f(x)=f(\pi )=\sin \pi =0 \] W \(-\infty\) funkcja dąży do osi \(x\)-ów, zatem: \[\lim_{x \to -\infty }f(x)=0 \] W \(+\infty\) funkcja nie ma granicy, ponieważ \(\sin x\) jest funkcją okresową i nie dąży do żadnej konkretnej wartości (tylko waha się w przedziale \((-1, 1)\)).