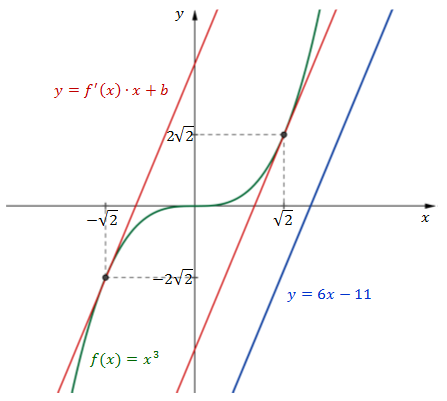Prosta styczna do wykresu funkcji \(f(x)\) w punkcie \(x_0\) ma współczynnik kierunkowy równy \(f'(x_0)\).
Inaczej mówiąc - równanie prostej stycznej do wykresu funkcji \(f(x)\) w punkcie \(x_0\) jest postaci: \[y=f'(x_0)\cdot x+b\] My chcemy wyznaczyć taki punkt \(x_0\) w którym styczna do wykresu funkcji \(f(x)\) będzie równoległa do prostej \(y=6x-11\). Proste są równoległe jeśli mają takie same współczynniki kierunkowe. Zatem styczna \(y=f'(x_0)\cdot x+b\) i prosta \(y=6x-11\) będą równoległe jeśli: \[f'(x_0)=6\] Żeby rozwiązać powyższe równanie, to musimy najpierw policzyć pochodną funkcji \(f(x)\): \[f'(x)=3x^2\] Zatem mamy: \[\begin{split} f'(x_0)&=6 \\[6pt] 3{x_0}^2&=6\\[6pt] {x_0}^2&=2\\[6pt] x_0=-\sqrt{2}\quad &\lor \quad x_0=\sqrt{2} \end{split}\] Zatem mamy dwa rozwiązania: \[\begin{split} \bigl(-\sqrt{2},\ f(-\sqrt{2})\bigl)\quad &\lor \quad \bigl(\sqrt{2},\ f(\sqrt{2})\bigl)\\[6pt] \bigl(-\sqrt{2},\ (-\sqrt{2})^3\bigl)\quad &\lor \quad \bigl(\sqrt{2},\ (\sqrt{2})^3\bigl)\\[6pt] \bigl(-\sqrt{2},\ -2\sqrt{2}\bigl)\quad &\lor \quad \bigl(\sqrt{2},\ 2\sqrt{2}\bigl) \end{split}\] Poniższy rysunek ilustruje sytuację z tego zadania: