Zbadaj granicę funkcji \(f(x)=\begin{cases} -x^2-3\quad \text{dla } x\le 0\\ \sqrt{x}-3 \quad \text{dla } x\gt 0 \end{cases} \) w punkcie \(x = 0\).
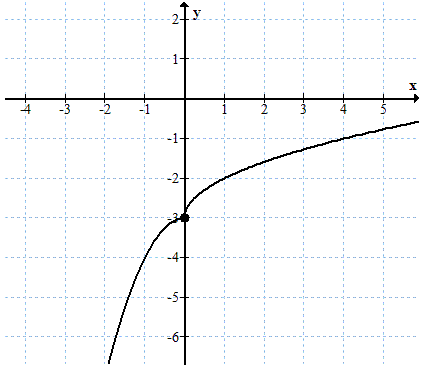Granica w punkcie \(x = 0\) istnieje, ponieważ granica lewostronna w tym punkcie jest równa prawostronnej: \[\begin{split} &\lim_{x \to 0^{-}}f(x)=-3\\[6pt] &\lim_{x \to 0^{+}}f(x)=-3 \end{split}\] Można zatem krótko napisać: \[\lim_{x \to 0}f(x)=-3\]Strony z tym zadaniem
Sąsiednie zadania
Zadanie 20054Zadanie 20055Zadanie 20056 (tu jesteś)
Zadanie 20057Zadanie 55234