Dany jest trapez prostokątny \(A B C D\) o kątach prostych przy wierzchołkach \(A\) i \(D\). Ramię \(B C\) trapezu ma długość \(5\) . W ten trapez wpisano okrąg o środku w punkcie \(S\) i promieniu \(2\). Punkt \(P\) jest punktem styczności tego okręgu i dłuższej podstawy \(A B\) tego trapezu (zobacz rysunek). 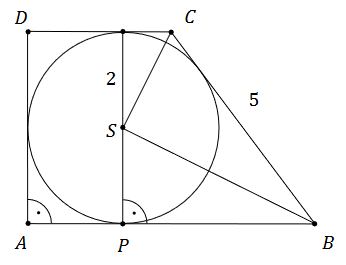
Wykaż, że trójkąty BPS i BSC są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa. Zapisz obliczenia.

Strony z tym zadaniem
Zadania maturalne CKE 2025 - poziom rozszerzonySąsiednie zadania
Zadanie 4339Zadanie 4340Zadanie 4341 (tu jesteś)
Zadanie 4347Zadanie 4348