Zadania maturalne CKE 2025 - poziom rozszerzony
Poziom rozszerzony
Nawigacja do bloków tematycznych:
Liczby rzeczywiste, wyrażenia algebraiczne, równania i nierówności, układy równań
Dany jest układ równań \[ \left\{\begin{array}{l} m x+y=m^{2} \tag{1}\\ 4 x+m y=8 \end{array}\right. \] z niewiadomymi \(x\) i \(y\) oraz parametrem \(m \in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(m\), dla których układ jest oznaczony, a para liczb \((x, y)\) będąca rozwiązaniem układu spełnia warunek \(|x+y|\lt2\). Zapisz obliczenia.
Dane są liczby \(a=\left(\log_{\sqrt{5}} 2\right) \cdot \log _{2} 25\) i \(b=\frac{\log_{5} 6}{\log_{5} 8}\).
Oblicz \(a^{b+1}\).
Na rysunku przedstawiono fragment wykresu wielomianu \(W\) określonego wzorem \[ W(x)=\frac{1}{8} x^{3}-2 x^{2}+\frac{67}{8} x-3 \] dla każdego \(x \in \mathbb{R}\). 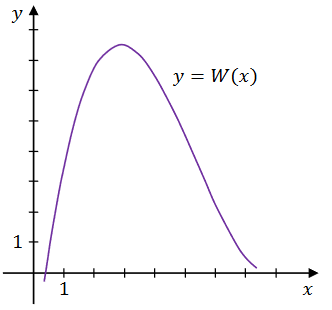

Oblicz wszystkie pierwiastki wielomianu \(W\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{-3 x+41}{x-13}\) dla każdej liczby rzeczywistej \(x \neq 13\).
Punktem kratowym nazywamy punkt w kartezjańskim układzie wspótrzędnych, którego obie współrzędne są liczbami całkowitymi.
Wyznacz wszystkie punkty kratowe należące do wykresu funkcji \(f\). Zapisz obliczenia.
Wielomian \(W\) jest określony wzorem \(W(x)=(x-1)\left(x^{2}-m x+m-1\right)\) dla każdego \(x \in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(\boldsymbol{m}\), dla których wielomian \(\boldsymbol{W}\) ma dokładnie jeden pierwiastek rzeczywisty. Zapisz obliczenia.
Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=p x^{2}+(p-1) x+1-2 p\) dla każdego \(x \in \mathbb{R}\).
Wyznacz wszystkie wartości parametru \(\boldsymbol{p}\), dla których funkcja \(\boldsymbol{f}\) ma dokładnie dwa miejsca zerowe różniące się o 1. Zapisz obliczenia.
Funkcje, ciągi, trygonometria, optymalizacja i rachunek różniczkowy
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{3x}{x+1}\) dla każdego \(x \in(-1,+\infty)\).
Wykaż, że \(f\) jest funkcją rosnącą.
Oblicz granice \(\lim _{n \rightarrow \infty} \sqrt[n]{6^{n}+7^{n}}\). Zapisz obliczenia.
Syzyf codziennie stoi przed zadaniem wtoczenia ciężkiej kamiennej kuli na szczyt pewnej góry.  W chwili \(t=0\) znajduje się on w punkcie \(\mathcal{O}\) oddalonym od szczytu o \(4\) km, a położenie \(x\) Syzyfa wtaczającego kulę jest opisane zależnością \[x(t)=-t^{3}+16,5 t^{2}+180 t\quad \text{dla}\quad t \in[0,24]\] gdzie \(x\) jest wyrażone w metrach, a \(t\)-w godzinach.
W chwili \(t=0\) znajduje się on w punkcie \(\mathcal{O}\) oddalonym od szczytu o \(4\) km, a położenie \(x\) Syzyfa wtaczającego kulę jest opisane zależnością \[x(t)=-t^{3}+16,5 t^{2}+180 t\quad \text{dla}\quad t \in[0,24]\] gdzie \(x\) jest wyrażone w metrach, a \(t\)-w godzinach.
Oś \(\mathcal{O} x\) jest skierowana do wierzchołka góry i jest styczna w każdym punkcie do zbocza góry.
 W chwili \(t=0\) znajduje się on w punkcie \(\mathcal{O}\) oddalonym od szczytu o \(4\) km, a położenie \(x\) Syzyfa wtaczającego kulę jest opisane zależnością \[x(t)=-t^{3}+16,5 t^{2}+180 t\quad \text{dla}\quad t \in[0,24]\] gdzie \(x\) jest wyrażone w metrach, a \(t\)-w godzinach.
W chwili \(t=0\) znajduje się on w punkcie \(\mathcal{O}\) oddalonym od szczytu o \(4\) km, a położenie \(x\) Syzyfa wtaczającego kulę jest opisane zależnością \[x(t)=-t^{3}+16,5 t^{2}+180 t\quad \text{dla}\quad t \in[0,24]\] gdzie \(x\) jest wyrażone w metrach, a \(t\)-w godzinach.Oś \(\mathcal{O} x\) jest skierowana do wierzchołka góry i jest styczna w każdym punkcie do zbocza góry.
Oblicz najmniejszą odległość, na jaką Syzyf zbliży się do wierzchołka góry, oraz największą prędkość, z jaką wtacza kamień pod górę. Zapisz obliczenia.
Cztery miasta \(A, B, C\) i \(D\) znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. (Przykład sieci dróg z dwoma węzłami, łączącej każde dwa z miast, przedstawiono na poniższym rysunku). 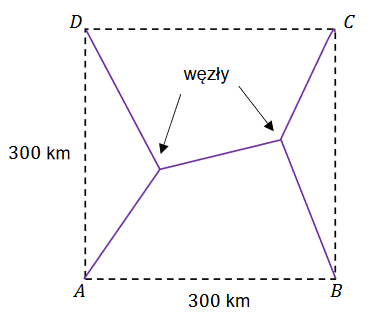

Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci. Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{2 x-3}{x+2}+4 \log _{\frac{1}{2}} x\) dla każdego \(x\gt 0\).
Wykaż, że funkcja \(\boldsymbol{f}\) ma co najmniej jedno miejsce zerowe, które należy do przedziału \(\left[\frac{1}{2}, 4\right]\).
Funkcja \(f\) jest określona wzorem \(f(x)=x^{4}+0,5 \cdot(2 x+1)^{4}\) dla każdego \(x \in \mathbb{R}\).
Oblicz najmniejszą wartość tej funkcji. Zapisz obliczenia.
W nieskończonym malejącym ciągu geometrycznym \(\left(a_{n}\right)\), określonym dla \(n \geq 1\), jest spełniony warunek \[ \frac{a_{5}+a_{3}}{a_{3}}=\frac{29}{25} \] Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa \(6\).
Wyznacz wzór ogólny na \(\boldsymbol{n}\)-ty wyraz ciągu \(\left(a_{n}\right)\). Zapisz obliczenia.
Funkcja \(f\) jest określona wzorem \(f(x)=x^{6}-2 x^{4}-x^{3}+1\) dla każdego \(x \in \mathbb{R}\).
Wykaż, że liczba \(5\) należy do zbioru wartości tej funkcji.
Rozwiąż równanie \[ (3-2 \cos x)^{2}=8 \sin ^{2}\left(\frac{x}{2}\right)-8 \cos ^{2}\left(\frac{x}{2}\right)+12 \] w zbiorze \((0, \pi)\). Zapisz obliczenia.
Wykaż, że równanie \(x^{4}-7 x^{3}+9 x^{2}+8 x-2=0\) ma w przedziale \((-2,2)\) co najmniej dwa różne rozwiązania.
Ciąg \(\left(a_{n}\right)\) jest określony wzorem \[ a_{n}=(n+5)^{2} \cdot\left(\frac{p+1}{(n+1)(n+2)}+\frac{2 p+2}{(n+2)(n+3)}\right) \] dla każdej liczby naturalnej \(n \geq 1\).
Wyznacz wszystkie wartości parametru \(p\), dla których granica ciągu ( \(a_{n}\) ) jest równa 12. Zapisz obliczenia.
Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa \(80\), pole powierzchni całkowitej jest równe \(256\) i długości wszystkich krawędzi są nie mniejsze niż \(4\).
Wykaż, że układ równań \[ \begin{align*} 4 a+4 b+4c & =80 \tag{1}\\ 2 ab+2 bc+2ca & =256 \tag{2} \end{align*} \] z niewiadomymi \(a\) oraz \(b\) ma rozwiązanie, które jest parą liczb rzeczywistych nie mniejszych od \(4\) wtedy i tylko wtedy, gdy \(c \in\left[4, \frac{28}{3}\right]\).
Objętość \(V\) każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji \[ V(c)=c^{3}-20 c^{2}+128 c \] gdzie \(c \in\left[4, \frac{28}{3}\right]\) jest długością jednej \(z\) krawędzi bryły.
Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza. Zapisz obliczenia.
Na rysunku obok przedstawiono położenie miejscowości \(A, B\) i \(C\) oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości \(A\) do \(C\) wyruszył zastęp harcerzy „Tropiciele" i przemieszczał się z prędkością \(4 \mathrm{~km} / \mathrm{h}\). O tej samej godzinie z miejscowości \(B\) do \(A\) wyruszył zastęp harcerzy „Korsarze" i przemieszczał się z prędkością \(2 \mathrm{~km} / \mathrm{h}\). 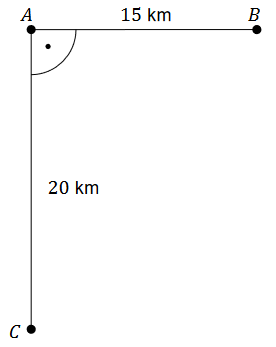

Wyznacz godzinę, o której odległość między tymi zastępami harcerzy będzie najmniejsza. Zapisz obliczenia.
Firma \(X\) wytwarza pewien produkt D. Badania rynku pokazały, że związek między ilością \(Q\) produktu \(D\), jaką firma jest w stanie zbyć na rynku, a ceną \(P\) produktu jest następujący: \[ P(Q)=90-0,1 Q \quad \text { dla } Q \in[0,900] \]
gdzie \(P\) jest ceną za jednostkę produktu w złotych, a \(Q\) - ilością produktu w tys. sztuk.
Koszty \(K\) wytworzenia produktu D zależą od ilości \(Q\) wytwarzanego produktu następująco: \[ K(Q)=0,002 Q^{3}+Q^{2}+29,9985 Q+50 \] gdzie \(K\) jest kosztem produkcji w tys. zł. Oblicz, przy jakiej wielkości produkcji firma X osiąga największy dochód. Wynik podaj zaokrąglony z dokładnością do 100 sztuk. Zapisz obliczenia.
Planimetria, geometria analityczna, stereometria
W ostrosłupie prawidłowym czworokątnym \(A B C D E\) punkt \(O\) jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy \(A B C D\) do sumy długości wszystkich krawędzi ostrosłupa jest równy \(1: 5\). Przez przekątną \(A C\) podstawy i środek \(S\) krawędzi bocznej \(B E\) poprowadzono płaszczyznę.
Skorzystaj z tablicy wartości funkcji trygonometrycznych (Wybrane wzory matematyczne, strona 34).
Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miare kąta BSO (w zaokrągleniu do \(1^{\circ}\) ). Zapisz obliczenia.
Wskazówka.Skorzystaj z tablicy wartości funkcji trygonometrycznych (Wybrane wzory matematyczne, strona 34).
W kartezjańskim układzie współrzędnych \((x, y)\) proste o równaniach \(2 x+y-4 m-4=0\) oraz \(x-3 y+5 m+5=0\) przecinają się w punkcie \(P\) o współrzędnych \(\left(x_{P}, y_{P}\right)\).
Wyznacz wszystkie wartości parametru \(m\), dla których współrzędne punktu \(P\) spełniają warunki: \[ x_{P}>0, y_{P}>0, y_{P} \geq x_{P}^{2} \quad \text { oraz } \quad 2<-\frac{8}{\left(y_{P}\right)^{2}}+\frac{8}{x_{P}} \] Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) trapez \(A B C D\) jest wpisany w okrąg o środku w punkcie \(S=(19,-11)\) i promieniu \(17 \sqrt{2}\). Wierzchołek \(A\) trapezu ma obie współrzędne ujemne, a odcinek \(A B\) jest dłuższą z podstaw tego trapezu. Przekątna \(A C\) trapezu \(A B C D\) jest zawarta w prostej o równaniu \(y=x\).
Oblicz sinus kąta \(A B C\). Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) czworokąt \(A B C D\) jest równoległobokiem takim, że \(\overrightarrow{B D}=[-21,-7]\) i \(\overrightarrow{D C}=[15,8]\).
Oblicz pole tego równoległoboku. Zapisz obliczenia.
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(a\). Punkt \(P\) jest środkiem krawędzi \(C G\) tego sześcianu (zobacz rysunek poniżej).  \[ |P G|=|P C| \]
\[ |P G|=|P C| \]
 \[ |P G|=|P C| \]
\[ |P G|=|P C| \] Oblicz odległość wierzchołka \(C\) od płaszczyzny zawierającej punkty \(B, D\) oraz \(P\). Zapisz obliczenia.
Dany jest trapez prostokątny \(A B C D\) o kątach prostych przy wierzchołkach \(A\) i \(D\). Ramię \(B C\) trapezu ma długość \(5\) . W ten trapez wpisano okrąg o środku w punkcie \(S\) i promieniu \(2\). Punkt \(P\) jest punktem styczności tego okręgu i dłuższej podstawy \(A B\) tego trapezu (zobacz rysunek). 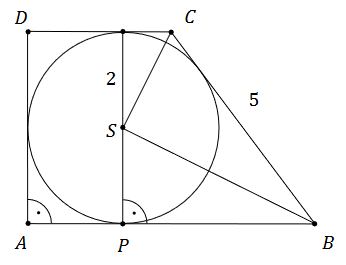
Wykaż, że trójkąty BPS i BSC są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa. Zapisz obliczenia.

Tomek i Marek chcą wejść docelowo na szczyt \(S\) pewnej góry. W chwili początkowej znajdują się w punkcie \(P\) położonym na stoku góry dokładnie na północ od szczytu na wysokości \(H_{0}\) metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy \(B\) znajdującej się dokładnie w połowie drogi na szczyt na południe od szczytu na przeciwległym południowym stoku góry na wysokości \(H_{1}\) metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości \(H_{2}\) metrów n.p.m. (zobacz rysunek 1.). 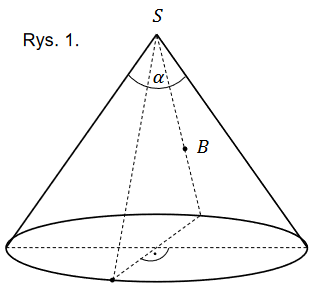

Oblicz długość najkrótszej drogi, jaką muszą pokonać, aby dotrzeć do bazy. Zapisz obliczenia.
Przyjmij, że góra jest stożkiem o kącie rozwarcia \(\alpha\).
Wskazówka: Powierzchnia boczna stożka po rozcięciu wzdłuż tworzącej i rozłożeniu jest wycinkiem koła. Najkrótsza droga do bazy odpowiada najkrótszej drodze z punktu \(P\) do \(B\) na wycinku koła. 

Kombinatoryka, rachunek prawdopodobieństwa, statystyka
Niech \(n\) będzie ustaloną liczbą naturalną dodatnią. Ze zbioru \(\mathbb{M}=\{1 ; 2 ; 3 ; \ldots ; 3 n+1\}\) losujemy jednocześnie trzy liczby. Zdarzenie \(A\) odpowiada jednoczesnemu wylosowaniu ze zbioru \(\mathbb{M}\) trzech liczb, których suma przy dzieleniu przez \(3\) daje resztę \(1\).
Oblicz prawdopodobieństwo zdarzenia \(\boldsymbol{A}\). Zapisz obliczenia.
Pan Nowak często gra z synem w szachy. Obliczył, że \(40 \%\) rozegranych z synem partii wygrywa.
Oblicz, ile partii szachów musi rozegrać z synem pan Nowak, aby prawdopodobieństwo wygrania przez ojca przynajmniej jednej partii w całej rozgrywce było większe od \(0,95\). Zapisz obliczenia.
Pewna choroba dotyka \(0,2 \%\) całej populacji i w początkowym stadium nie daje widocznych objawów chorobowych. W ramach profilaktyki stosuje się pewien test przesiewowy, który daje wynik pozytywny lub negatywny. Prawdopodobieństwo tego, że test wykonany na osobie chorej da wynik pozytywny (oznaczający chorobę), jest równe \(0,99\). Ponadto wiadomo, że prawdopodobieństwo tego, że test wykonany na osobie zdrowej da wynik negatywny, jest równe \(0,98\).
Pan X poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby.
Pan X poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby.
Oblicz prawdopodobieństwo tego, że pan X jest rzeczywiście chory. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych. Zapisz obliczenia.
W pewnym mieście jest prostopadły układ ulic, a ruch na każdej z nich jest dwukierunkowy. W centrum miasta znajduje się park, gdzie obowiązuje całkowity zakaz ruchu pojazdów. Schemat ulic w tym mieście wraz z położeniem parku przedstawiono poniżej na rysunku. Tomek znajduje się w punkcie \(A\) miasta i chce dojechać samochodem najkrótszą drogą do punktu \(B\). 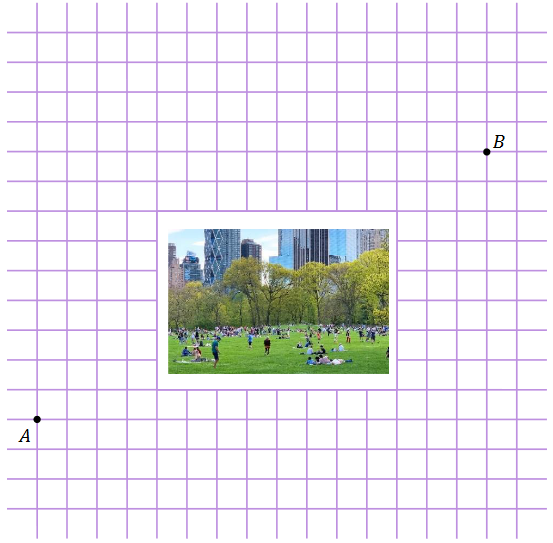
Oblicz, ile jest najkrótszych dróg z \(A\) do \(B\). Zapisz obliczenia.

Tematy nadrzędne i sąsiednie