Dany jest sześcian \(ABCDEFGH\) o krawędzi długości \(6\). Punkt \(S\) jest punktem przecięcia przekątnych \(AH\) i \(DE\) ściany bocznej \(ADHE\) (zobacz rysunek). 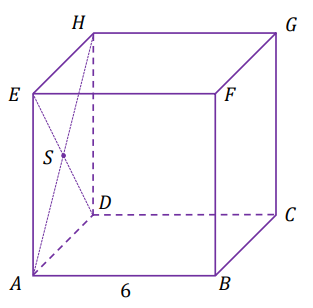

Oblicz wysokość trójkąta \(SBH\) poprowadzoną z punktu \(S\) na bok \(BH\) tego trójkąta. Zapisz obliczenia.
Strony z tym zadaniem
Matura 2023 maj PRSąsiednie zadania
Zadanie 3873Zadanie 3874Zadanie 3875 (tu jesteś)
Zadanie 3876Zadanie 3877