Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Wysokość \(SE\) ściany bocznej \(ADS\) jest jednocześnie wysokością ostrosłupa, a punkt \(E\) jest środkiem krawędzi \(AD\) (zobacz rysunek). Pole ściany \(ADS\) jest równe \(12\) cm2, a objętość ostrosłupa jest równa \(48\) cm3. Oblicz miarę kąta nachylenia krawędzi bocznej \(CS\) do płaszczyzny podstawy ostrosłupa. Wynik zaokrąglij do \(1^\circ \). 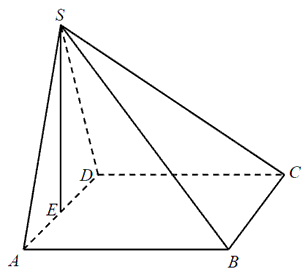

Strony z tym zadaniem
Matura 2012 marzec 9Różne zadania z ostrosłupówMatura podstawowa z matematyki - kurs - geometria przestrzennaMatura podstawowa - kurs - część 55 - zadaniaSąsiednie zadania
Zadanie 365Zadanie 366Zadanie 367 (tu jesteś)
Zadanie 368Zadanie 369