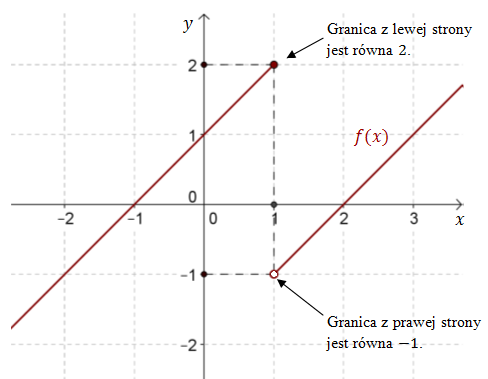
Widzimy, że dla argumentu \(x_0=1\) funkcja jest nieciągła.
Jeżeli zbliżamy się z argumentami \(x\) do \(x_0=1\) z lewej strony, to wartości funkcji dążą do \(2\). Jeśli natomiast zbliżamy się z argumentami \(x\) do \(x_0=1\) z prawej strony, to wartości funkcji dążą do \(-1\). Zatem w punkcie \(x_0=1\) funkcja \(f(x)\) nie ma granicy.

Funkcja \(f(x)\) ma w punkcie \(x_0=1\) granicę lewostronną i prawostronną.
Granica lewostronna jest równa \(2\) i zapisujemy to w taki sposób: \[\lim_{x \to 1^{-}}f(x)=2 \] Granica prawostronna jest równa \(-1\) i zapisujemy to w taki sposób: \[\lim_{x \to 1^{+}}f(x)=-1 \] Granica lewostronna i prawostronna są różne, zatem funkcja \(f(x)\) nie ma granicy w punkcie \(x_0=1\).