Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3 : 4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\). Oblicz objętość ostrosłupa. 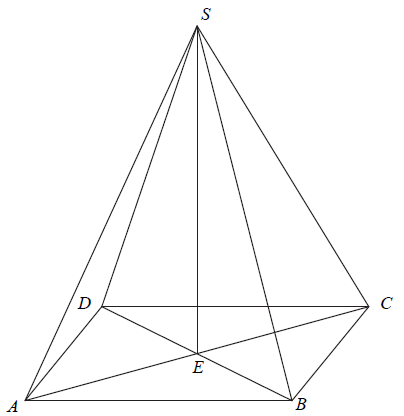

Strony z tym zadaniem
Matura 2015 sierpieńPewniaki maturalneRóżne zadania z ostrosłupówMatura podstawowa - kurs - część 55 - zadaniaMatura podstawowa - kurs - część 59 - zadaniaSąsiednie zadania
Zadanie 1754Zadanie 1755Zadanie 1756 (tu jesteś)
Zadanie 1757Zadanie 1758