Matura podstawowa - kurs - część 59 - zadania

Drukuj

Poziom podstawowy

Cały kurs na: http://www.matemaks.pl/matematyka-matura-podstawowa-kurs.html.

Kąt \(\alpha \) nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku: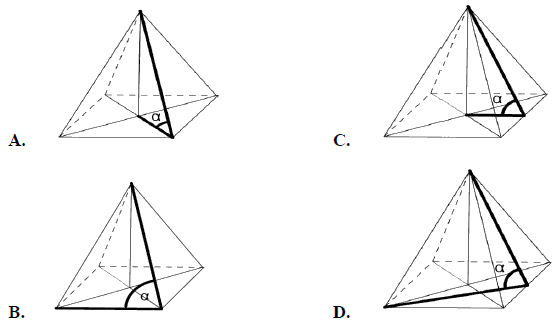

Podstawą ostrosłupa \(ABCDE\) jest kwadrat \(ABCD\). Punkt \(F\) jest środkiem krawędzi \(AD\), odcinek \(EF\) jest wysokością ostrosłupa (patrz rysunek). Oblicz objętość ostrosłupa, jeśli wiadomo, że \(|AE|=15\), \(|BE|=17\).

\(\frac{64\sqrt{209}}{3}\)

W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) i wierzchołku \(S\) trójkąt \(ACS\) jest równoboczny i ma bok długości \(8\). Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).

\(\sin \alpha =\frac{\sqrt{42}}{7}\)

Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest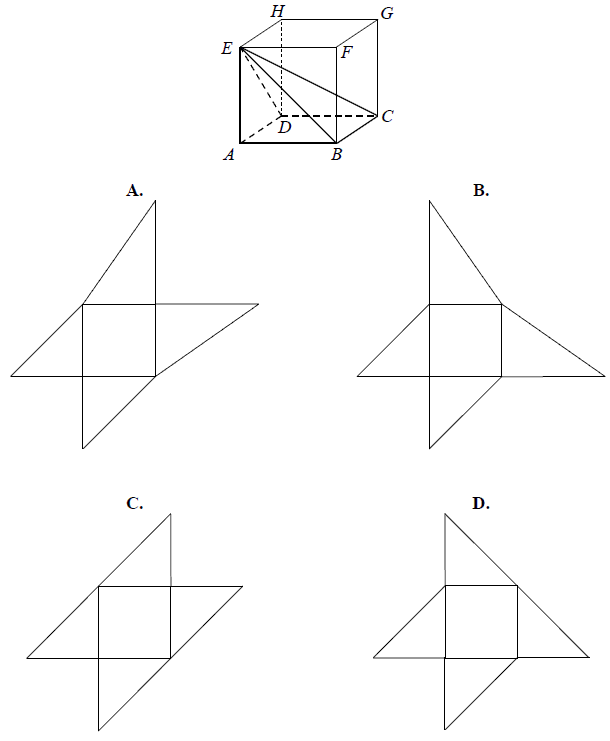

Ostrosłup ma \(18\) wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa

A.\( 11 \)

B.\( 18 \)

C.\( 27 \)

D.\( 34 \)

Podstawą ostrosłupa \(ABCD\) jest trójkąt \(ABC\). Krawędź \(AD\) jest wysokością ostrosłupa (zobacz rysunek).

Oblicz objętość ostrosłupa \(ABCD\), jeśli wiadomo, że \(AD = 12\), \(BC = 6\), \(BD = CD = 13\).

\(V=48\)

Graniastosłup ma \(2n+6\) wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa

A.\( n+3 \)

B.\( 4n+8 \)

C.\( 6n+18 \)

D.\( 3n+9 \)

W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa \(90\). Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe

A.\( 300 \)

B.\( 300\sqrt{3} \)

C.\( 300+50\sqrt{3} \)

D.\( 300+25\sqrt{3} \)

W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość \(5\) cm, a krawędź podstawy \(\sqrt{8}\) cm. Wówczas cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy:

A.\( \frac{\sqrt{2}}{5} \)

B.\( 0{,}6 \)

C.\( 0{,}4 \)

D.\( \frac{\sqrt{8}}{10} \)

Przekątna graniastosłupa prawidłowego czworokątnego \(ABCDA_1B_1C_1D_1\) ma długość \(2\sqrt{219}\), a krawędź podstawy - \(10\sqrt{2}\).

Wyznacz:

Wysokość graniastosłupa.
Pole trójkąta \(EFG\), którego wierzchołkami są środki trzech krawędzi wychodzących z jednego wierzchołka podstawy.

\(H=2\sqrt{119}\), \(P_{\Delta EFG}=60\)

Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ\). Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa \(4\). Oblicz objętość tego ostrosłupa.

\(V=\frac{128\sqrt{3}}{3}\)

Graniastosłup ma \(15\) krawędzi. Ile wierzchołków ma ten graniastosłup?

A.\( 10 \)

B.\( 5 \)

C.\( 15 \)

D.\( 30 \)

Objętość graniastosłupa prawidłowego trójkątnego o wysokości \(7\) jest równa \(28\sqrt{3}\) . Długość krawędzi podstawy tego graniastosłupa jest równa

A.\( 2 \)

B.\( 4 \)

C.\( 8 \)

D.\( 16 \)

Liczba wszystkich krawędzi graniastosłupa jest równa \(24\). Wtedy liczba wszystkich jego wierzchołków jest równa

A.\( 6 \)

B.\( 8 \)

C.\( 12 \)

D.\( 16 \)

W graniastosłupie prawidłowym czworokątnym \( ABCDEFGH \) połączono punkty będące środkami krawędzi \( BC \), \( CD \), \( AD \) i \( GH \). Wyznacz objętość powstałej bryły wiedząc, że \( \vert{DB}\vert=5\sqrt{2} \) i kąt \( DBH \) ma miarę \( 60^\circ \).

\(V=\frac{125\sqrt{6}}{12}\)

Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa \( 22 \), a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy \( \frac{4\sqrt{6}}{5} \). Oblicz objętość tego ostrosłupa.

\(V=\frac{3200\sqrt{6}}{3}\)

Rysunek przedstawia ostrosłup prawidłowy czworokątny \(ABCDS\).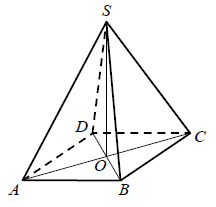

Kątem między krawędzią \(CS\) a płaszczyzną podstawy tego ostrosłupa jest kąt

A.\( DCS \)

B.\( ACS \)

C.\( OSC \)

D.\( SCB \)

Każda krawędź graniastosłupa prawidłowego trójkątnego ma długość równą \(8\). Pole powierzchni całkowitej tego graniastosłupa jest równe

A.\( 8^2\left ( \frac{\sqrt{3}}{2}+3 \right ) \)

B.\( \frac{8^2\sqrt{6}}{3} \)

C.\( 8^2\cdot \sqrt{3} \)

D.\( \frac{8^2}{3}\left ( \frac{\sqrt{3}}{2}+3 \right ) \)

Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.

\(P=144+384\sqrt{2}\)

Podstawą ostrosłupa \(ABCDS\) jest prostokąt, którego boki pozostają w stosunku \(3 : 4\), a pole jest równe \(192\) (zobacz rysunek). Punkt \(E\) jest wyznaczony przez przecinające się przekątne podstawy, a odcinek \(SE\) jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ\). Oblicz objętość ostrosłupa.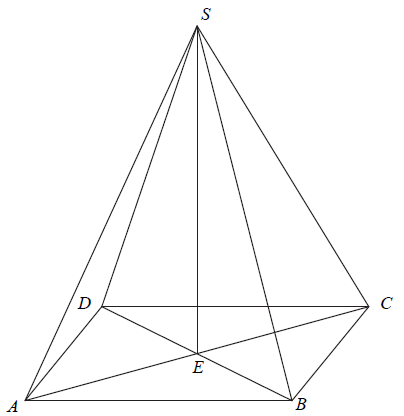

\(V=\frac{640\sqrt{3}}{3}\)

Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość \(9\) (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa

A.\( 3\sqrt{6} \)

B.\( 3\sqrt{3} \)

C.\( 2\sqrt{6} \)

D.\( 3\sqrt{2} \)