Drukuj
Naszkicuj i oblicz pole figury ograniczonej wykresami: \[\begin{split}y&=x^2-2x-3\\y&=x+1\\y&=-3x+9\end{split}\] dla \(x\in \left \langle -1, 3\right \rangle\).
Na początku rysujemy wykresy wszystkich trzech funkcji i znajdujemy ich punkty przecięcia: 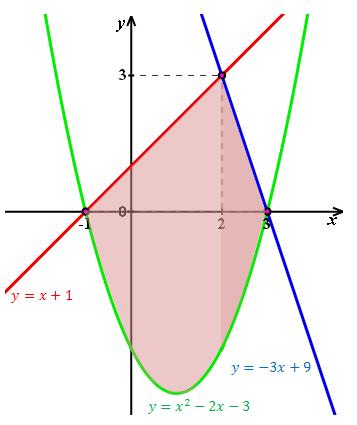 Szukane pole zostało zamalowane kolorem czerwonym (część jaśniejszym, a część ciemniejszym). Obliczymy oddzielnie pole ograniczone krzywymi dla \(x\in \left \langle -1, 2 \right \rangle\) oraz dla \(x\in \left \langle 2, 3 \right \rangle\).
Szukane pole zostało zamalowane kolorem czerwonym (część jaśniejszym, a część ciemniejszym). Obliczymy oddzielnie pole ograniczone krzywymi dla \(x\in \left \langle -1, 2 \right \rangle\) oraz dla \(x\in \left \langle 2, 3 \right \rangle\).
Na początku obliczymy pole zamalowane kolorem jaśniejszym, czyli ograniczone krzywymi \(y=x+1\) oraz \(\ y=x^2-2x-3\ \) w przedziale dla \(x\in \left \langle -1, 2 \right \rangle\): Teraz obliczymy pole zamalowane kolorem ciemniejszym, czyli ograniczone krzywymi \(y=-3x+9\) oraz \(\ y=x^2-2x-3\ \) w przedziale dla \(x\in \left \langle 2, 3 \right \rangle\): Zatem całe pole jest równe: \[13{,}5+\frac{19}{6}=\frac{27}{2}+\frac{19}{6}=\frac{81}{6}+\frac{19}{6}=\frac{100}{6}\] Odpowiedź: Pole ograniczone krzywymi jest równe \(\frac{100}{6}\).
 Szukane pole zostało zamalowane kolorem czerwonym (część jaśniejszym, a część ciemniejszym). Obliczymy oddzielnie pole ograniczone krzywymi dla \(x\in \left \langle -1, 2 \right \rangle\) oraz dla \(x\in \left \langle 2, 3 \right \rangle\).
Szukane pole zostało zamalowane kolorem czerwonym (część jaśniejszym, a część ciemniejszym). Obliczymy oddzielnie pole ograniczone krzywymi dla \(x\in \left \langle -1, 2 \right \rangle\) oraz dla \(x\in \left \langle 2, 3 \right \rangle\).Na początku obliczymy pole zamalowane kolorem jaśniejszym, czyli ograniczone krzywymi \(y=x+1\) oraz \(\ y=x^2-2x-3\ \) w przedziale dla \(x\in \left \langle -1, 2 \right \rangle\):
\[\begin{split}&\int\limits_{-1}^{2} x+1\ dx - \int\limits_{-1}^{2} x^2-2x-3\ dx=\\&=\int\limits_{-1}^{2} x+1-x^2+2x+3\ dx=\\&=\int\limits_{-1}^{2}-x^2+3x+4\ dx=\\&=\left [ -\frac{x^3}{3}+\frac{3x^2}{2}+4x \right ]_{-1}^{2}=\\&=-\frac{2^3}{3}+\frac{3\cdot 2^2}{2}+4\cdot 2 -\left ( -\frac{(-1)^3}{3}+\frac{3\cdot (-1)^2}{2}+4\cdot (-1)\right )=\\&=-\frac{8}{3}+6+8-\left ( \frac{1}{3}+\frac{3}{2}-4 \right )=\\&=-\frac{8}{3}+14-\frac{1}{3}-1{,}5+4=13{,}5\end{split}\]
\[\begin{split}&\int\limits_{2}^{3} -3x+9\ dx - \int\limits_{2}^{3} x^2-2x-3\ dx=\int\limits_{2}^{3} -3x+9-x^2+2x+3\ dx=\\&=\int\limits_{2}^{3}-x^2-x+12\ dx=\\&=\left [ -\frac{x^3}{3}-\frac{x^2}{2}+12x \right ]_{2}^{3}=\\&=-\frac{3^3}{3}-\frac{3^2}{2}+12\cdot 3 - \left ( -\frac{2^3}{3}-\frac{2^2}{2}+12\cdot 2 \right )=\\&=-9-\frac{9}{2}+36-\left ( -\frac{8}{3}-2+24 \right )=\\&=22{,}5+\frac{8}{3}-22=\frac{1}{2}+\frac{8}{3}=\frac{19}{6}\end{split}\]
Strony z tym zadaniem
Sąsiednie zadania
Zadanie 1721003Zadanie 1721004Zadanie 1721005 (tu jesteś)
© 2010-2024 Matemaks | Na górę strony | Kontakt | Regulamin | Polityka prywatności | Informacje o koncie premium | Strona główna