Wyrażenia algebraiczne w geometrii

Drukuj

Szkoła podstawowa

Wyrażenia algebraiczne są bardzo przydatne w geometrii, ponieważ pozwalają zapisywać wzory np. na pola i obwody figur.

Prostokąt o bokach \(a\) oraz \(b\) ma pole \(P=a\cdot b\) oraz obwód \(O=2a+2b\).
Trójkąt o podstawie \(x\) i wysokości \(y\) ma pole \(P=\frac{1}{2}x\cdot y\).
Trójkąt o bokach długości \(a, b, c\) ma obwód \(O=a+b+c\).

Zapisz wzór na pole i obwód prostokąta o bokach długości \(5x+1\) oraz \(x+y\).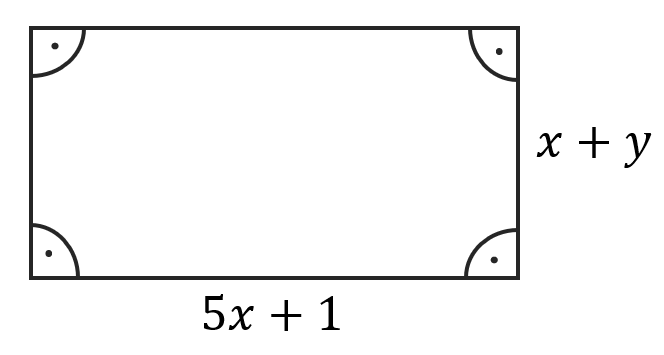

Wzór na pole to:

\(P=(5x+1)(x+y)\) \(=5x^2+5xy+x+y\)

Wzór na obwód to:

\(O=2\cdot (5x+1+x+y)\) \(=2\cdot (6x+y+1)\) \(=12x+2y+1\)

Zapisz wzór na pole trójkąta o podstawie \(3y\) oraz wysokości \(3x\). Następnie oblicz to pole dla \(x=5\) oraz \(y=7\).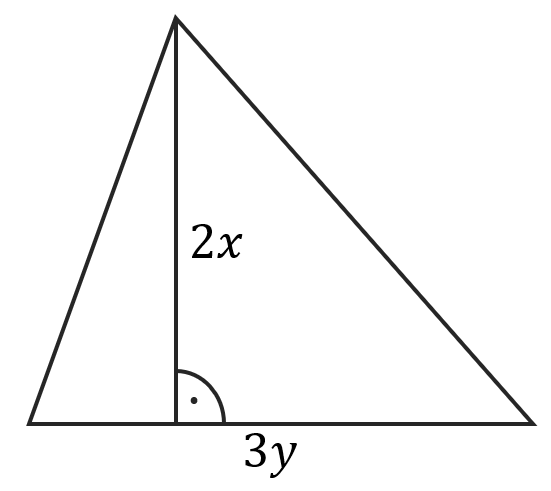

Wzór na pole to: \[P=\frac{1}{2}\cdot 2x\cdot 3y=3xy\] Dla \(x=5\) oraz \(y=7\) mamy: \[P=3xy=3\cdot 5\cdot 7=105\]

Zapisz w najprostszej postaci obwody prostokątów o bokach długości:

Zapisz w najprostszej postaci obwody prostokątów o bokach długości:

\(O=2[(3x-2)+(x+4)] \) \(= 2(3x-2+x+4) \) \(= 2(4x+2) \) \(= 8x+4 \) \(= 4(2x+1)\)
\(O=2[(2x+5)+(3x-1)] \) \(= 2(2x+5+3x-1) \) \(= 2(5x+4) \) \(= 10x+8\)
\(O=2[(x^2+2x)+(2x-3)] \) \(= 2(x^2+2x+2x-3) \) \(= 2(x^2+4x-3) \) \(= 2x^2+8x-6\)

Zapisz w najprostszej postaci pola prostokątów o bokach długości:

\(P=(2x+3)(x-1)\) \(=2x\cdot x+2x\cdot(-1)+3\cdot x+3\cdot(-1)\) \(=2x^2-2x+3x-3\) \(=2x^2+x-3\)
\(P=(3x-2)(2x+5)\) \(=3x\cdot2x+3x\cdot5-2\cdot2x-2\cdot5\) \(=6x^2+15x-4x-10\) \(=6x^2+11x-10\)
\(P=(x^2+1)(3x-4)\) \(=x^2\cdot3x+x^2\cdot(-4)+1\cdot3x+1\cdot(-4)\) \(=3x^3-4x^2+3x-4\)

Zapisz w najprostszej postaci pole trapezu, którego dwie podstawy i wysokość są wyrażone za pomocą wyrażeń algebraicznych.

Pole trapezu wyraża się wzorem: \[ P=\frac{1}{2}(a+b)h. \] Dla podstaw \(a=2x+3\) i \(b=x-1\) oraz wysokości \(h=3x+2\): \[ \begin{split} P &= \frac{1}{2}\Bigl[(2x+3)+(x-1)\Bigr](3x+2)\\[6pt] &= \frac{1}{2}(3x+2)(3x+2)\\[6pt] &= \frac{1}{2}(9x^2+12x+4)\\[6pt] &= \frac{9x^2}{2}+6x+2. \end{split} \]
Dla podstaw \(a=3x-2\) i \(b=2x+5\) oraz wysokości \(h=4x-1\): \[ \begin{split} P &= \frac{1}{2}\Bigl[(3x-2)+(2x+5)\Bigr](4x-1)\\[6pt] &= \frac{1}{2}(5x+3)(4x-1)\\[6pt] &= \frac{1}{2}\Bigl[20x^2 -5x +12x -3\Bigr]\\[6pt] &= \frac{1}{2}(20x^2+7x-3)\\[6pt] &= 10x^2+\frac{7}{2}x-\frac{3}{2}. \end{split} \]
Dla podstaw \(a=x^2+1\) i \(b=2x-3\) oraz wysokości \(h=x+4\): \[ \begin{split} P &= \frac{1}{2}\Bigl[(x^2+1)+(2x-3)\Bigr](x+4)\\[6pt] &= \frac{1}{2}(x^2+2x-2)(x+4)\\[6pt] &= \frac{1}{2}\Bigl[x^3+4x^2+2x^2+8x-2x-8\Bigr]\\[6pt] &= \frac{1}{2}(x^3+6x^2+6x-8)\\[6pt] &= \frac{x^3}{2}+3x^2+3x-4. \end{split} \]

Zapisz w najprostszej postaci za pomocą wyrażeń algebraicznych obwód i pole poniższego wielokąta, którego sąsiednie boki są prostopadłe.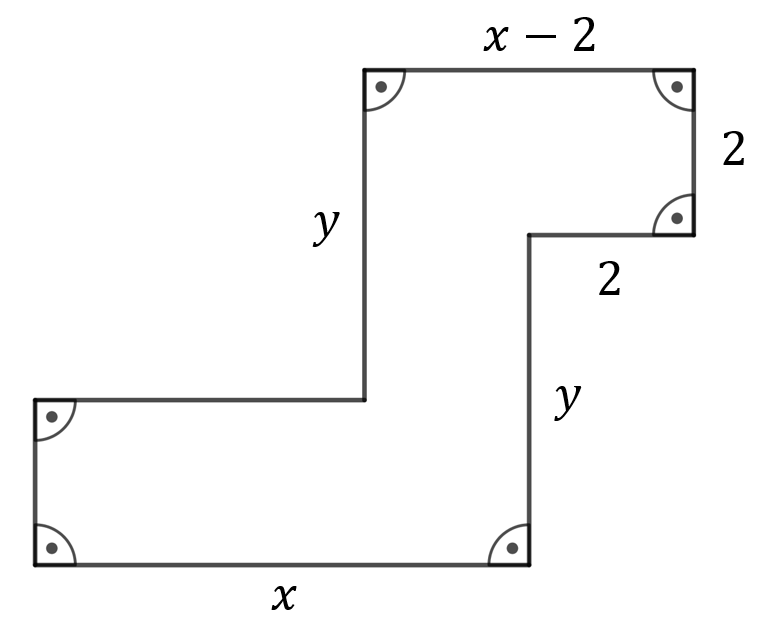

\(Ob = 2x+2y+8\)
\(P=xy+2x-4y+4\)

Długości boków czworokąta opisano za pomocą wyrażeń algebraicznych, tak jak pokazano na rysunku.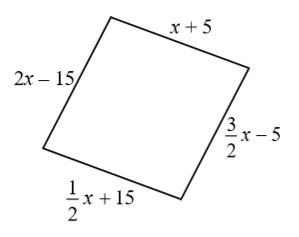

Uzasadnij, że jeśli obwód tego czworokąta jest równy \(100\) cm, to jest on rombem. Zapisz obliczenia.

Na rysunku przedstawiono prostokąt o bokach długości \(a\) i \(b\) podzielony na sześć kwadratów.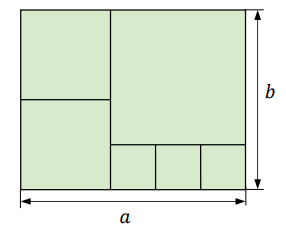

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.

Stosunek długości boków \(a:b\) tego prostokąta jest równy

A.\( 6:5 \)

B.\( 5:4 \)

C.\( 4:3 \)

D.\( 3:2 \)