Sumowanie wyrażeń algebraicznych

Drukuj

Szkoła podstawowa

Suma algebraiczna – to suma w której występują liczby i zmienne. Poszczególne składniki takiej sumy nazywamy wyrazami.

Oto przykład sumy algebraicznej: \[3x^2+2x-5-3x+1\] Wyrazy tej sumy to: \(3x^2\), \(2x\), \(-5\), \(-3x\) oraz \(1\).

Zauważ, że wyrazy sumy bierzemy razem ze znakiem.

Wyrazy sumy algebraicznej: \[5xy-x^2-y^2+3xy\] to: \(5xy\), \(-x^2\), \(-y^2\) oraz \(3xy\).

Sumę algebraiczną można uprościć, jeżeli ma wyrazy podobne.

Wyrazy podobne – to wyrazy, które mają te same zmienne w tych samych potęgach.

Wyrazy podobne nazywamy też czasami jednomianami podobnymi (to pojęcie jest jednak obecnie rzadziej stosowane).

Wyrazy podobne mogą różnić się jedynie współczynnikiem liczbowym.

Współczynnik liczbowy – to liczba stojąca przed zmienną, np.: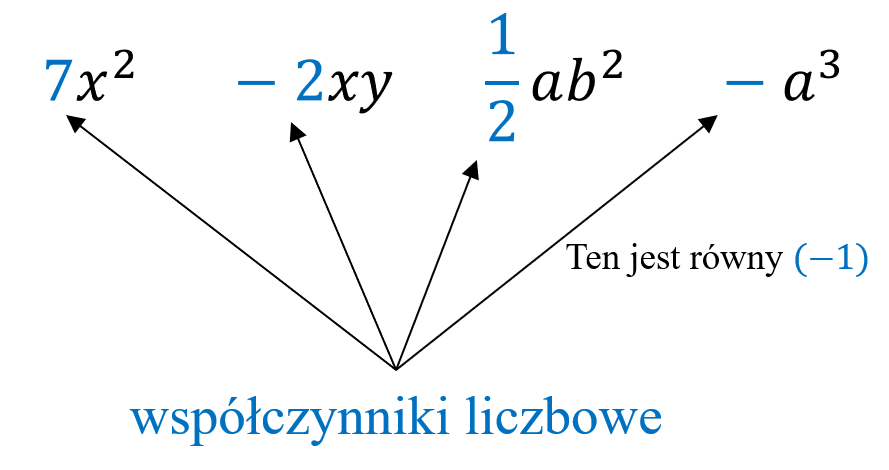

Jeżeli przed zmienną nie ma liczby, to oznacza, że współczynnik jest równy \(1\).
Jeżeli przed zmienną stoi sam minus, to oznacza, że współczynnik jest równy \(-1\).

Wyrazy: \[x,\quad 3x,\quad \frac{3}{4}x,\quad -5x,\quad \sqrt{2}x\] są podobne, ponieważ wszystkie są postaci: \[\text{liczba} \cdot x\]

Wyrazy: \[3x^2y,\quad -x^2y,\quad 6x^2y,\quad \frac{1}{3}x^2y\] są podobne, ponieważ wszystkie są postaci: \[\text{liczba} \cdot x^2y\]

Wyrazy: \[a^5b^3c,\quad 7^5b^3c^4,\quad -90abc\] nie są podobne, ponieważ każdy ma inną część złożoną z literek.

Wśród wyrazów: \[5x,\quad 3x^2,\quad \frac{1}{2}x,\quad 3x,\quad -x^2,\quad 2x^3\] wskaż wyrazy podobne.

Wyrazy podobne pierwszego stopnia, to: \[5x,\quad \frac{1}{2}x,\quad 3x\] Wyrazy podobne drugiego stopnia, to: \[3x^2,\quad -x^2\]

Wyrazy podobne możemy dodawać, np: \[3x^2+4x^2=7x^2\] Wyrazów, które nie są podobne nie możemy dodawać.

Dodawanie wyrazów podobnych upraszcza wyrażenie algebraiczne i często jest nazywane redukcją wyrazów podobnych.

Zredukuj wyrazy podobne i uprość wyrażenie:

Wszystkie wyrazy są podobne, więc je dodajemy:
\[5x-x+3x+6x=(5-1+3+6)x=13x\]

\[\begin{split}&5x-x+3x+6x=\\[6pt]&=(5-1+3+6)x=13x\end{split}\]
Wyszukujemy wyrazy podobne i dodajemy je:
\[\color{red}{3x^2}+\color{blue}{2x}+\color{red}{5x^2}-\color{blue}{x}= \color{red}{3x^2}+\color{red}{5x^2}+\color{blue}{2x}-\color{blue}{x}= \color{red}{8x^2}+\color{blue}{x}\]

\[\begin{split}&\color{red}{3x^2}+\color{blue}{2x}+\color{red}{5x^2}-\color{blue}{x}=\\[6pt] &=\color{red}{3x^2}+\color{red}{5x^2}+\color{blue}{2x}-\color{blue}{x}=\\[6pt] &=\color{red}{8x^2}+\color{blue}{x}\end{split}\]
Wyszukujemy wyrazy podobne i dodajemy je:
\[\color{red}{3x^3y} -4xy \color{red}{-4x^3y}+1= \color{red}{3x^3y} \color{red}{-4x^3y} -4xy +1= \color{red}{-x^3y}-4xy +1\]

\[\begin{split}&\color{red}{3x^3y} -4xy \color{red}{-4x^3y}+1=\\[6pt] &=\color{red}{3x^3y} \color{red}{-4x^3y} -4xy +1=\\[6pt] &=\color{red}{-x^3y}-4xy +1\end{split}\]

Nazwy wyrażeń algebraicznych możemy zapisać słownie według znaków działań, które je łączą, np.:

Zapis matematyczny	Zapis słowny
\(x + y\)	suma liczb \(x\) i \(y\)
\(x - y\)	różnica liczb \(x\) i \(y\)
\(x\cdot y\)	iloczyn liczb \(x\) i \(y\)
\(x : y\)	iloraz liczb \(x\) i \(y\)
\(2x\)	podwojona liczba \(x\)
\(3x\)	liczba trzy razy większa od \(x\)
\(0{,}5x\)	połowa liczby \(x\)
\(x - 12\)	liczba o \(12\) mniejsza od \(x\)
\(x^2\)	kwadrat liczby \(x\)
\(x^2 + y^2\)	suma kwadratów liczb \(x\) i \(y\)
\((x + y)^2\)	kwadrat sumy liczb \(x\) i \(y\)
\(x^3 - y^3\)	różnica sześcianów liczb \(x\) i \(y\)
(\(2x)^2 - 0{,}5y^3\)	różnica kwadratu podwojonej liczby \(x\) i połowy sześcianu liczby \(y\)

W tym nagraniu wideo pokazuję jak dodawać wyrażenia algebraiczne.

Zredukuj wyrazy podobne.

\(4x-2x+3x\)
\(-x-2x+7x\)
\(-a+a-a\)
\(2a^2-a^2+3a^2\)
\(xy-2xy-5xy\)
\(ab^2+2ab^2+10ab^2\)

\(4x-2x+3x=(4-2+3)x=5x\)
\(-x-2x+7x=(-1-2+7)x=4x\)
\(-a+a-a=(-1+1-1)a=-a\)
\(2a^2-a^2+3a^2\) \(=(2-1+3)a^2=4a^2\)
\(xy-2xy-5xy\) \(=(1-2-5)xy=-6xy\)
\(ab^2+2ab^2+10ab^2\) \(=(1+2+10)ab^2\) \(=13ab^2\)

Zredukuj wyrazy podobne.

\(x+1+y-3x-2y+5+3\)
\(2x-4+3y+5-6x+2-2y\)
\(4x+7-2y-3+5x-9+y\)
\(3x+2y+8-x+4-2y+5\)
\(6x-3y+10-2x+y-5+x-3\)
\(7x+3y+2-4x-y-5+x-1\)

\(x+1+y-3x-2y+5+3 \) \(= (x-3x) + (y-2y) + (1+5+3) \) \(= -2x - y + 9\)
\(2x-4+3y+5-6x+2-2y \) \(= (2x-6x) + (3y-2y) + (-4+5+2) \) \(= -4x + y + 3\)
\(4x+7-2y-3+5x-9+y \) \(= (4x+5x) + (-2y+y) + (7-3-9) \) \(= 9x - y - 5\)
\(3x+2y+8-x+4-2y+5 \) \(= (3x-x) + (2y-2y) + (8+4+5) \) \(= 2x + 17\)
\(6x-3y+10-2x+y-5+x-3 \) \(= (6x-2x+x) + (-3y+y) + (10-5-3) \) \(= 5x - 2y + 2\)
\(7x+3y+2-4x-y-5+x-1 \) \(= (7x-4x+x)+(3y-y)+(2-5-1) \) \(= 4x+2y-4\)

Zredukuj wyrazy podobne.

\(3x^3+2x^2+5x+4y-x^3-3y\)
\(4x^2-2x+7y+3x-5y+x^2\)
\(2x^3+4x- y+3x^2+5y-6x\)
\(5a^3-2a^2+3a+4b^2-a^3-3b^2\)
\(4a^2+7b-3a+2a^2-5b+a\)
\(3a^3+2a+4b^2-2a^3-2b^2+5b\)
\(2p^3+3p^2+4p+5q-p^3-3p\)
\(4p^2-2p+6q+3p^2+p-4q\)

\(3x^3+2x^2+5x+4y-x^3-3y\) \(=(3x^3-x^3)+2x^2+5x+(4y-3y)\) \(=2x^3+2x^2+5x+y\)
\(4x^2-2x+7y+3x-5y+x^2\) \(=(4x^2+x^2)+(-2x+3x)+(7y-5y)\) \(=5x^2+x+2y\)
\(2x^3+4x-y+3x^2+5y-6x\) \(=2x^3+3x^2+(4x-6x)+(-y+5y)\) \(=2x^3+3x^2-2x+4y\)
\(5a^3-2a^2+3a+4b^2-a^3-3b^2\) \(=(5a^3-a^3)+(-2a^2)+3a+(4b^2-3b^2)\) \(=4a^3-2a^2+3a+b^2\)
\(4a^2+7b-3a+2a^2-5b+a\) \(=(4a^2+2a^2)+(-3a+a)+(7b-5b)\) \(=6a^2-2a+2b\)
\(3a^3+2a+4b^2-2a^3-2b^2+5b\) \(=(3a^3-2a^3)+2a+(4b^2-2b^2)+5b\) \(=a^3+2a+2b^2+5b\)
\(2p^3+3p^2+4p+5q-p^3-3p\) \(=(2p^3-p^3)+3p^2+(4p-3p)+5q\) \(=p^3+3p^2+p+5q\)
\(4p^2-2p+6q+3p^2+p-4q\) \(=(4p^2+3p^2)+(-2p+p)+(6q-4q)\) \(=7p^2-p+2q\)

Zredukuj wyrazy podobne.

\(3x^2y-3+x^2y-xy\)
\(ab-b+ab-a\)
\(4xy+3x^2y-2xy+x^2y\)
\(5a^2b-3ab+2a^2b+ab\)
\(3pq^2-2pq+4pq^2-pq\)
\(2m^2n+3mn-m^2n-4mn\)
\(6xy-2x^2y+3xy-x^2y+5\)
\(7ab^2-4ab+2ab^2+ab\)

\(3x^2y-3+x^2y-xy = (3x^2y+x^2y)-xy-3 = 4x^2y-xy-3\)
\(ab-b+ab-a = (ab+ab)-(a+b) = 2ab-a-b\)
\(4xy+3x^2y-2xy+x^2y = (4xy-2xy)+(3x^2y+x^2y) = 2xy+4x^2y\)
\(5a^2b-3ab+2a^2b+ab = (5a^2b+2a^2b)+(-3ab+ab) = 7a^2b-2ab\)
\(3pq^2-2pq+4pq^2-pq = (3pq^2+4pq^2)+(-2pq-pq) = 7pq^2-3pq\)
\(2m^2n+3mn-m^2n-4mn = (2m^2n-m^2n)+(3mn-4mn) = m^2n-mn\)
\(6xy-2x^2y+3xy-x^2y+5 = (6xy+3xy)+(-2x^2y-x^2y)+5 = 9xy-3x^2y+5\)
\(7ab^2-4ab+2ab^2+ab = (7ab^2+2ab^2)+(-4ab+ab) = 9ab^2-3ab\)

Nazwij wyrażenie algebraiczne.