Skracanie wyrażeń wymiernych

Drukuj

Poziom podstawowy

Wyrażenia wymierne skracamy tak samo jak ułamki - dzielimy licznik i mianownik przez to samo wyrażenie.

Uwaga! Jeżeli skracamy wyrażenia wymierne, to musimy założyć, że wyrażenie przez które dzielimy licznik i mianownik jest różne od zera.

Uprość wyrażenie wymierne \(\frac{15}{3x^2}\).

Licznik i mianownik ułamka możemy podzielić przez \(3\): \[\frac{15}{3x^2}=\frac{15:3}{3x^2:3}=\frac{5}{x^2}\] Dziedzina tego wyrażenia wymiernego, to: \(\mathbb{R} \backslash \{0\}\).

Uprość wyrażenie wymierne \(\frac{7}{21x}\).

Licznik i mianownik ułamka możemy podzielić przez \(7\): \[\frac{7}{21x}=\frac{7:7}{21x:7}=\frac{1}{3x}\] Dziedzina tego wyrażenia wymiernego, to: \(\mathbb{R} \backslash \{0\}\).

Uprość wyrażenie wymierne \(\frac{x(x+4)}{2x}\).

Dziedzina tego wyrażenia to: \(\mathbb{R} \backslash \{0\}\).
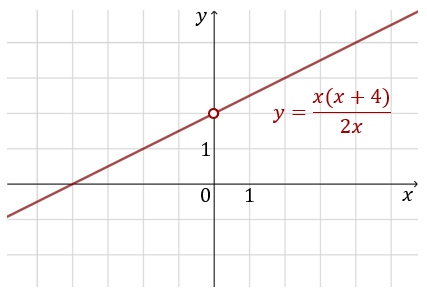
Mając ustaloną dziedzinę możemy podzielić licznik i mianownik przez \(x\): \[\frac{x(x+4)}{2x}=\frac{x+4}{2}=\frac{1}{2}x+2\] Zatem wyrażenie \(\frac{x(x+4)}{2x}\) jest równoważne wyrażeniu liniowemu \(\frac{1}{2}x+2\), ale określonemu na dziedzinie: \(\mathbb{R} \backslash \{0\}\).
Czyli wykres funkcji \(y=\frac{x(x+4)}{2x}\) wyglądałby tak:

Uprość wyrażenie wymierne \(\frac{6(x+1)(x-3)}{5(x-3)(x-4)}\).

Licznik i mianownik ułamka możemy podzielić przez \((x-3)\). Wcześniej musimy określić dziedzinę, ponieważ będziemy dzielić przez wyrażenie z \(x\)-em. Wyznaczamy dziedzinę, czyli szukamy miejsc zerowych mianownika: \[\begin{split} 5(x-3)(x-4)&= 0\\[6pt] (x-3)(x-4)&=e 0\\[6pt] x-3= 0\quad &\lor \quad x-4= 0\\[6pt] x= 3 \quad &\lor \quad x= 4 \end{split}\] Czyli dziedzina tego wyrażenia wymiernego, to: \(\mathbb{R} \backslash \{3,4\}\). Teraz możemy wykonać skrócenie ułamka: \[\frac{6(x+1)(x-3)}{5(x-3)(x-4)}=\frac{6(x+1)(x-3):(x-3))}{5(x-3)(x-4):(x-3)}=\frac{6(x+1)}{5(x-4)}\] Zatem po skróceniu otrzymujemy postać: \(\frac{6(x+1)}{5(x-4)}\) o dziedzinie: \(\mathbb{R} \backslash \{3,4\}\).

Wyrażenie \(\frac{x^{-2}+x^{-3}}{x^{-3}-x^{-2}}\), gdzie \(x \ne 0\) i \(x \ne 1\) , po uproszczeniu może mieć postać:

A.\( \frac{x+1}{1-x} \)

B.\( \frac{x-1}{x+1} \)

C.\( \frac{x+2}{x-1} \)

D.\( \frac{1+x}{x} \)

Po skróceniu ułamek \(\frac{2x^2-4x}{x-2}\) dla \(x \ne 2\) jest równy

A.\( 2x^2-2 \)

B.\( 2x \)

C.\( x^2-2 \)

D.\( x-2 \)

Uprość wyrażenie wymierne: \(\frac{x^2+x-2}{x^2-1}\).

\(\frac{x+2}{x+1}\)

Dodatnie liczby \(x\) i \(y\) spełniają warunek \(2x=3y\). Wynika stąd, że wartość wyrażenia \(\frac{x^2+y^2}{x\cdot y}\) jest równa

A.\( \frac{2}{3} \)

B.\( \frac{13}{6} \)

C.\( \frac{6}{13} \)

D.\( \frac{3}{2} \)

Dane są dwie liczby \(x\) i \(y\), takie, że iloraz \(\frac{x}{y}\) jest równy \(\frac{1+\sqrt{5}}{2}\).

Oblicz wartość wyrażenia \(\frac{x+y}{x}\). Wynik podaj bez niewymierności w mianowniku.

\(\frac{1+\sqrt{5}}{2}\)