Równania liniowe
Poziom podstawowy
Równanie - to dwa wyrażenia algebraiczne połączone znakiem równości.
Każde równanie ma lewą stronę i prawą stronę.
Każde równanie ma lewą stronę i prawą stronę.
Przykładowe równanie: 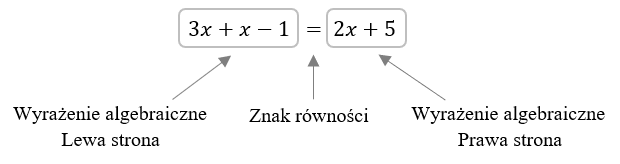

Rozwiązanie równania - to taka liczba \(x\), która po podstawieniu do równania da lewą stronę równą prawej.
Równanie liniowe z jedną niewiadomą \(x\) - to równanie, które można doprowadzić do postaci: \[ax+b=0\] Jeżeli \(a\ne 0\), to rozwiązaniem takiego równania jest liczba: \[x=-\frac{b}{a}\]
Rozwiązywanie równania liniowego polega na przekształcaniu go do równań równoważnych, w taki sposób, żeby po jednej jego stronie została tylko niewiadoma \(x\), a po drugiej stronie tylko liczba. Przekształcanie równania polega na: - Dodawanie lub odejmowanie od obu stron równania takiej samej liczby (lub wyrażenia z \(x\)-em).
- Dzielenie lub mnożenie obu stron równania przez taką samą liczbę.
Rozwiąż równanie \(3x+x-1=2x+5\).
Na początku uprościmy lewą stronę równania dodając wyrażenia z \(x\)-em: \[\begin{split} 3x+x-1&=2x+5\\[6pt] 4x-1&=2x+5 \end{split}\] Teraz od obu stron równania odejmiemy wyrażenie \(2x\), żeby po prawej stronie pozbyć się wyrażeń z \(x\)-em. \[\begin{split} 4x-1\color{Red}{-2x} &=2x+5\color{Red}{-2x} \\[6pt] 2x-1&=5 \end{split}\] Teraz do obu stron równania dodamy liczbę \(1\), żeby po lewej stronie zostało samo wyrażenie z \(x\)-em. \[\begin{split} 2x-1\color{Red}{+1} &=5\color{Red}{+1} \\[6pt] 2x&=6 \end{split}\] Teraz dzielimy obie strony równania przez liczbę \(2\), żeby po lewej stronie został sam \(x\). \[\begin{split} \qquad 2x&=6\qquad //:2\\[6pt] x&=3 \end{split}\] Odpowiedź: Rozwiązaniem równania jest liczba \(x = 3\).
Rozwiąż równanie \(\frac{x+3}{2}=2-\frac{x-2}{4}\).
Mnożymy obie strony równania przez \(4\). \[ \begin{split} \frac{x+3}{2}&=2-\frac{x-2}{4} \qquad /\cdot 4\\[6pt] 2(x+3)&=8-(x-2) \\[6pt] 2x+6&=8-x+2 \\[6pt] 2x+x&=10-6 \\[6pt] 3x&=4 \\[6pt] x&=\frac{4}{3} \end{split} \] Odpowiedź: Rozwiązaniem równania jest liczba \(x = \frac{4}{3}\).
Nagranie z 2011 roku, w którym pokazuję jak rozwiązywać równania liniowe.
Rozwiązaniem równania \(3(2-3x)=x-4\) jest
A.\( x=1 \)
B.\( x=2 \)
C.\( x=3 \)
D.\( x=4 \)
Która z liczb jest rozwiązaniem równania \(5x-7=0\cdot (x+11)-2\cdot (1-3x)\)?
A.\( 5 \)
B.\( -5 \)
C.\( 6 \)
D.\( -1 \)
Która z liczb jest rozwiązaniem równania \(2(x-1)+x=x-3(2-3x)\)?
A.\( \frac{8}{11} \)
B.\( -\frac{4}{11} \)
C.\( \frac{4}{7} \)
D.\( -1 \)
Rozwiązanie równania \(x(x+3)-49=x(x-4)\) należy do przedziału
A.\( (-\infty ,3) \)
B.\( (10,+\infty ) \)
C.\( (-5,-1) \)
D.\( (2,+\infty ) \)
Rozwiązaniem równania \(-2=\frac{x-1}{x+2}\) jest liczba
A.\( -1 \)
B.\( 1 \)
C.\( 0 \)
D.\( \frac{5}{3} \)
Rozwiązaniem równania \( \frac{x-3}{2-x}=\frac{1}{2} \) jest liczba:
A.\(-\frac{4}{3} \)
B.\(-\frac{3}{4} \)
C.\(\frac{3}{8} \)
D.\(\frac{8}{3} \)
Rozwiąż równanie \(\frac{2-3x}{1-2x}=-\frac{1}{2}\).
Rozwiązaniem równania \(\frac{3x-1}{7x+1}=\frac{2}{5}\) jest
A.\( 1 \)
B.\( \frac{7}{3} \)
C.\( \frac{4}{7} \)
D.\( 7 \)
Rozwiązaniem równania \( \frac{x-5}{7-x}=\frac{1}{3} \) jest liczba
A.\(-11 \)
B.\(\frac{11}{2} \)
C.\(\frac{2}{11} \)
D.\(11 \)
Rozwiązaniem równania \(\frac{2x-4}{3-x}=\frac{4}{3}\) jest liczba
A.\( x=0 \)
B.\( x=\frac{12}{5} \)
C.\( x=2 \)
D.\( x=\frac{25}{11} \)
Równość \(\frac{m}{5-\sqrt{5}}=\frac{5+\sqrt{5}}{5}\) zachodzi dla
A.\( m=-5 \)
B.\( m=1 \)
C.\( m=4 \)
D.\( m=5 \)