Przesunięcie wykresu funkcji kwadratowej \(f(x)=ax^2\) o wektor

Poziom podstawowy

Wykres funkcji \(f(x)=2x^2+3\) otrzymamy, przesuwając parabolę \(y=2x^2\) o \(3\) jednostki do góry, czyli o wektor \(\vec{v}=[0,3]\).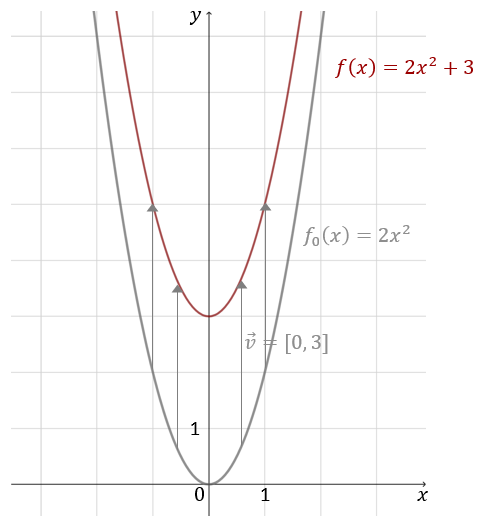

Wykres funkcji \(f(x)=2x^2-3\) otrzymamy, przesuwając parabolę \(y=2x^2\) o \(3\) jednostki w dół, czyli o wektor \(\vec{v}=[0,-3]\).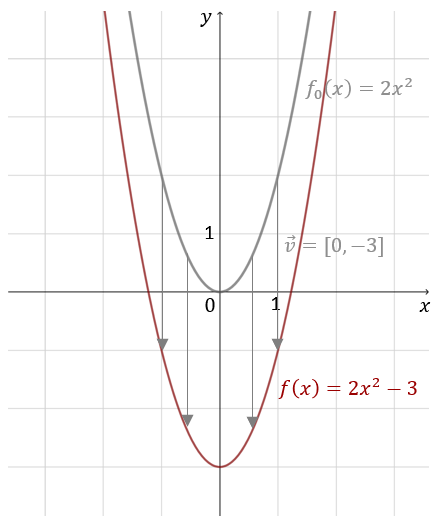

Wykres funkcji \(f(x)=2(x-3)^2\) otrzymamy, przesuwając parabolę \(y=2x^2\) o \(3\) jednostki w prawo, czyli o wektor \(\vec{v}=[3,0]\).

Wykres funkcji \(f(x)=2(x+3)^2\) otrzymamy, przesuwając parabolę \(y=2x^2\) o \(3\) jednostki w lewo, czyli o wektor \(\vec{v}=[-3,0]\).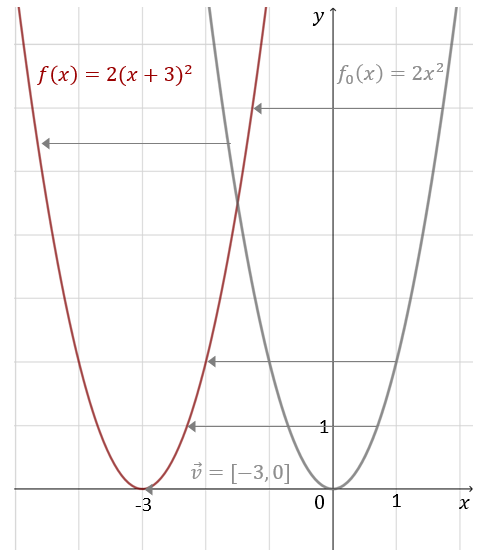

Wykres funkcji \(f(x)=a(x-p)^2+q\) otrzymamy, przesuwając parabolę \(y=2x^2\) o \(p\) jednostek w poziomie i o \(q\) jednostek w pionie, czyli o wektor \(\vec{v}=[p,q]\).

Wierzchołkiem paraboli będącej wykresem funkcji \(f\) jest punkt \((p, q)\). Jej osią symetrii jest prosta \(x=p\).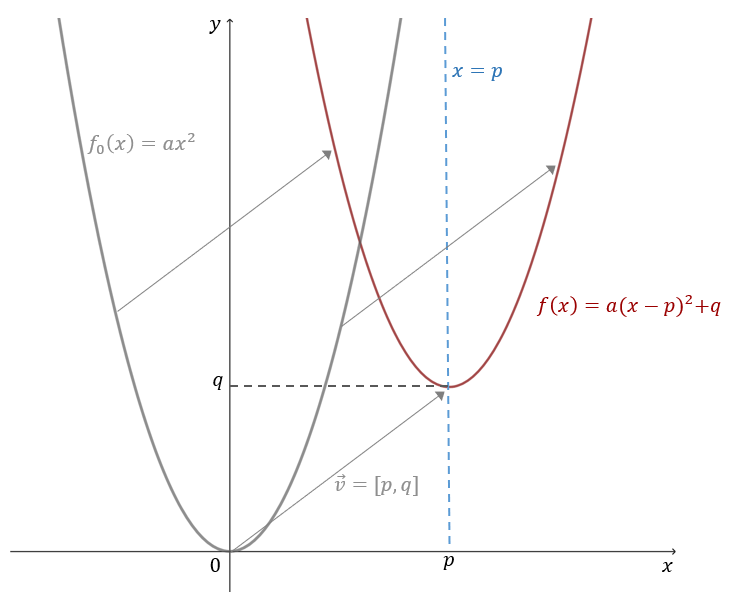

O jaki wektor należy przesunąć parabolę daną wzorem \(y=x^2\), aby otrzymać wykres funkcji:

\(f(x)=(x-2)^2+3\)

\(f(x)=(x+5)^2-4\)

\(f(x)=(x+1)^2+2\)

\(\vec{v}=[2,3]\)

\(\vec{v}=[-5,-4]\)

\(\vec{v}=[-1,2]\)

Funkcję \(g\) otrzymano z przesunięcia funkcji \(f\) o wektor \(\vec{v}\). Wyznacz wzór funkcji \(g\).

\(f(x)=x^2\) i \(\vec{v}=[-3,-4]\)

\(f(x)=-2x^2\) i \(\vec{v}=[1,2]\)

\(f(x)=\frac{1}{3}x^2\) i \(\vec{v}=\left[-5,\frac{1}{7}\right]\)

\(f(x)=-x^2\) i \(\vec{v}=[\sqrt{2},-\sqrt{3}]\)

\(g(x)=(x-(-3))^2-4=(x+3)^2-4\)

\(g(x)=-2(x-1)^2+2\)

\(g(x)=\frac{1}{3}(x-(-5))^2+\frac{1}{7}=\frac{1}{3}(x+5)^2+\frac{1}{7}\)

\(g(x)=-(x-\sqrt{2})^2-\sqrt{3}\)