Funkcja kwadratowa typu \(f(x)=ax^2\)
Poziom podstawowy
Definicja
Funkcja kwadratowa - to funkcja którą można zapisać wzorem: \[ f(x)=ax^2+bx+c \] gdzie \(a, b, c\) są współczynnikami liczbowymi i \(a \ne 0\). Wykres funkcji kwadratowej nazywamy parabolą.
W tym rozdziale zajmiemy się najprostszą funkcją kwadratową, którą określa wzór: \[f(x)=ax^2\]
Rozważmy wykres funkcji \(f(x)=x^2\).
Wykres możemy naszkicować obliczając wartości funkcji dla wybranych argumentów \(x\):
Zatem: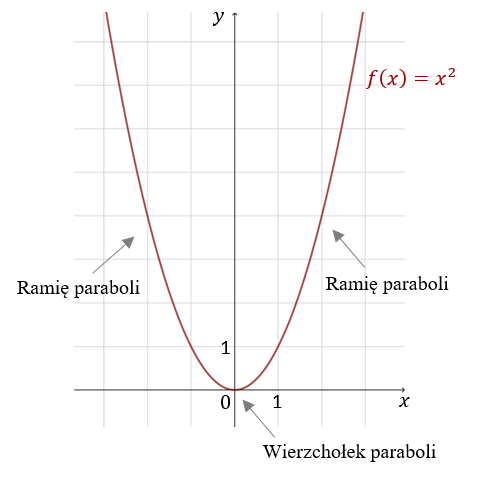 
Z wykresu można odczytać następujące własności:
Wykres możemy naszkicować obliczając wartości funkcji dla wybranych argumentów \(x\):
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)=x^2\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Z wykresu można odczytać następujące własności: - Dziedzinę: \(x\in \mathbb{R} \).
- Zbiór wartości: \(\langle 0, +\infty )\).
- Ramiona są skierowane do góry.
- Punkt \((0,0)\) jest wierzchołkiem paraboli.
- W wierzchołku funkcja przyjmuje wartość najmniejszą.
- Funkcja nie przyjmuje wartości największej.
- Oś \(y\)-ów jest osią symetrii paraboli.
- Funkcja jest malejąca w przedziale \((-\infty ,0\rangle \) i rosnąca w przedziale \(\langle 0,+\infty )\).
Wierzchołek dzieli parabolę na dwie części, które nazywamy ramionami paraboli.
Ramiona paraboli będącej wykresem funkcji kwadratowej \(f(x)=ax^2\) rozchylają się w różny sposób w zależności od wartości współczynnika \(a\).
Wykresy funkcji \(f(x)=ax^2\) dla różnych dodatnich współczynników \(a\):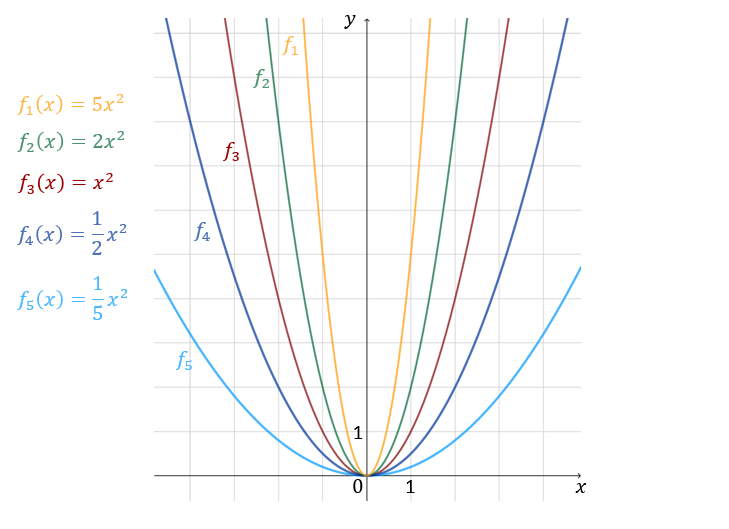 
Wszystkie parabole dla \(a\gt 0\) mają ramiona skierowane do góry.
Wszystkie parabole dla \(a\gt 0\) mają ramiona skierowane do góry. Wykresy funkcji \(f(x)=ax^2\) dla różnych ujemnych współczynników \(a\): 
Wszystkie parabole dla \(a\lt 0\) mają ramiona skierowane do dołu.
Wszystkie parabole dla \(a\lt 0\) mają ramiona skierowane do dołu. Współczynnik \(a\) we wzorze funkcji \(f(x)=ax^2\) decyduje o tym, czy ramiona paraboli skierowane są do góry (dla \(a\gt 0)\)), czy do dołu (dla \(a\lt 0)\) oraz o ich rozchyleniu.
Przeanalizujmy jeszcze dokładnie funkcję \(f(x)=-x^2\).
Wykres możemy naszkicować obliczając wartości funkcji dla wybranych argumentów \(x\):
Zatem: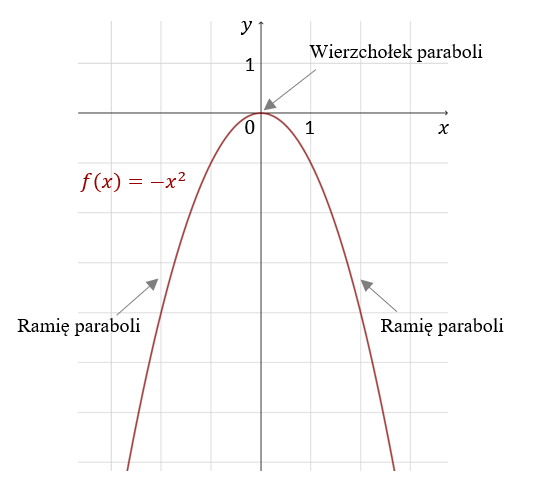 
Z wykresu można odczytać następujące własności:
Wykres możemy naszkicować obliczając wartości funkcji dla wybranych argumentów \(x\):
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)=x^2\) | \(-4\) | \(-1\) | \(0\) | \(-1\) | \(-4\) |
Z wykresu można odczytać następujące własności: - Dziedzinę: \(x\in \mathbb{R} \).
- Zbiór wartości: \((-\infty, 0\rangle \).
- Ramiona są skierowane do dołu.
- Punkt \((0,0)\) jest wierzchołkiem paraboli.
- W wierzchołku funkcja przyjmuje wartość największą.
- Funkcja nie przyjmuje wartości najmniejszej.
- Oś \(y\)-ów jest osią symetrii paraboli.
- Funkcja jest rosnąca w przedziale \((-\infty ,0\rangle \) i malejąca w przedziale \(\langle 0,+\infty )\).
Naszkicuj wykres funkcji \(f(x)\) o dziedzinie \(D\). Podaj zbiór wartości oraz określ wartość największą oraz najmniejszą dla tej funkcji.
\(f(x)=3x^2, \quad D=(-1 ; 2)\)
\(f(x)=-\frac{1}{4}x^2, \quad D=\langle -3; 1)\)
\(f(x)=-3x^2, \quad D=\left\langle -5 ; \frac{1}{2}\right\rangle \)
Punkt \(P\) należy do wykresu funkcji \(f(x)=ax^2\). Oblicz wartość funkcji \(f\) dla argumentu \(x=2\).
\(P=\left(3,-\frac{3}{2}\right)\)
\(P=\left(-2,8\sqrt{2}\right)\)
Prosta \(y=3\) przecina parabolę \(y=ax^2\) w punktach \(A\) i \(B\). Oblicz \(a\), jeśli:
\(|AB|=2\)
\(|AB|=6\sqrt{2}\)