Postać ogólna funkcji kwadratowej
Poziom podstawowy
Definicja
Postać ogólna funkcji kwadratowej to: \[ f(x)=ax^2+bx+c \] gdzie \(a, b, c\) są współczynnikami liczbowymi i \(a \ne 0\).Ważne wzory
Z postaci ogólnej funkcji kwadratowej można obliczyć wyróżnik trójmianu kwadratowego, czyli Deltę: \[ \Delta =b^2-4ac \] Jeżeli \(\Delta\gt 0\), to można obliczyć dwa miejsca zerowe: \[ {x}_{1}=\frac{-b-\sqrt{\Delta }}{2a}\quad \lor \quad {x}_{2}=\frac{-b+\sqrt{\Delta }}{2a}\] Jeżeli \(\Delta = 0\), to jest tylko jedno miejsce zerowe: \(x = \frac{-b}{2a}\).Jeżeli \(\Delta \lt 0\), to funkcja nie ma miejsc zerowych.
Dla dowolnej delty można obliczyć współrzędne wierzchołka \(W=(p,q)\): \[p=\frac{-b}{2a}\quad \text{oraz} \quad q=\frac{-\Delta }{4a}\]
- czy ramiona paraboli są skierowane do góry (gdy \(a > 0\)), czy do dołu (gdy \(a < 0\)),
- punkt przecięcia paraboli z osią \(OY\), który ma współrzędne \((0, c)\).
Dla funkcji kwadratowej \(f(x)=x^2-4x-5\) oblicz miejsca zerowe oraz współrzędne wierzchołka, naszkicuj wykres, wyznacz zbiór wartości i przedziały monotoniczności.
Współczynniki liczbowe tej funkcji to: \[a=1, \quad b=-4, \quad c=-5\] Liczymy deltę: 
Z wykresu odczytujemy:
\(\Delta =b^2-4ac=(-4)^2-4\cdot 1\cdot (-5)\ \)\(=16+20=36\)
Delta jest dodatnia, czyli funkcja ma dwa miejsca zerowe: \(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-4)-\sqrt{36}}{2\cdot 1}\ \)\(=\frac{4-6}{2}=-1\)
oraz \[x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{4+6}{2}=5\] Liczymy współrzędne wierzchołka \(W=(p,q)\): \[p=\frac{-b}{2a}=\frac{-(-4)}{2\cdot 1}=\frac{4}{2}=2\] oraz \[q=\frac{-\Delta }{4a}=\frac{-36}{4\cdot 1}=-9\] Zatem: \[W=(2,-9)\] Możemy już naszkicować wykres: Z wykresu odczytujemy: - Zbiór wartości: \(\langle -9, +\infty )\).
- Przedział w którym funkcja maleje: \(x\in (-\infty ,2\rangle \).
- Przedział w którym funkcja rośnie: \(x\in \langle 2, +\infty )\).
Dla funkcji kwadratowej \(f(x)=4x^2+6x+3\) oblicz miejsca zerowe oraz współrzędne wierzchołka, naszkicuj wykres, wyznacz zbiór wartości i przedziały monotoniczności.
Współczynniki liczbowe tej funkcji to: \[a=4, \quad b=6, \quad c=3\] Liczymy deltę:
Liczymy współrzędne wierzchołka \(W=(p,q)\): \[p=\frac{-b}{2a}=\frac{-6)}{2\cdot 4}=-\frac{3}{4}\] oraz \[q=\frac{-\Delta }{4a}=\frac{12}{4\cdot 4}=\frac{3}{4}\] Zatem: \[W=\left(-\frac{3}{4}, \frac{3}{4}\right)\] Możemy już naszkicować wykres: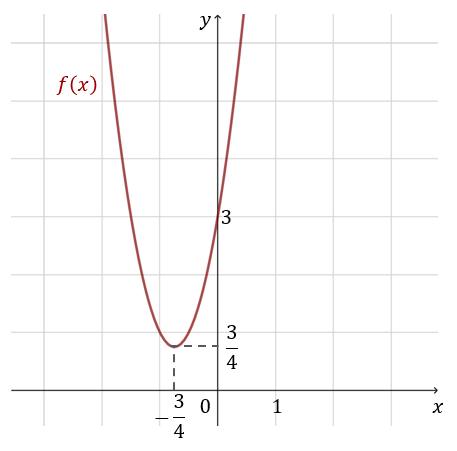
Z wykresu odczytujemy:
\(\Delta =b^2-4ac=6^2-4\cdot 4\cdot 3\ \)\(=36-48=-12\)
Delta wyszła ujemna, czyli funkcja nie ma miejsc zerowych.Liczymy współrzędne wierzchołka \(W=(p,q)\): \[p=\frac{-b}{2a}=\frac{-6)}{2\cdot 4}=-\frac{3}{4}\] oraz \[q=\frac{-\Delta }{4a}=\frac{12}{4\cdot 4}=\frac{3}{4}\] Zatem: \[W=\left(-\frac{3}{4}, \frac{3}{4}\right)\] Możemy już naszkicować wykres:
Z wykresu odczytujemy: - Zbiór wartości: \(\left\langle \frac{3}{4}, +\infty \right)\).
- Przedział w którym funkcja maleje: \(x\in \left(-\infty ,-\frac{3}{4}\right\rangle \).
- Przedział w którym funkcja rośnie: \(x\in \left\langle -\frac{3}{4}, +\infty \right)\).
Rysunek obok przedstawia wykres funkcji kwadratowej \( f \). Zapisz wzór funkcji \( f \) w postaci ogólnej i podaj jej zbiór wartości.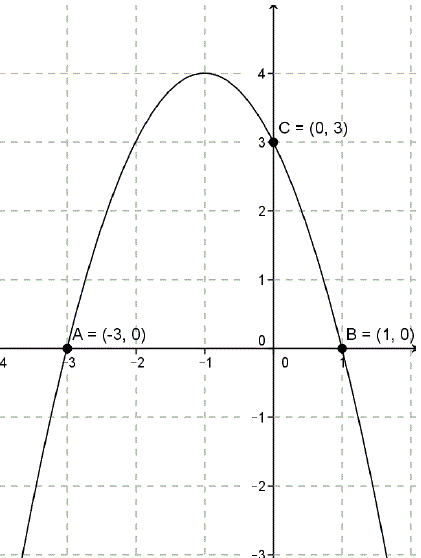 
Funkcja kwadratowa określona jest wzorem \(f(x)=x^2+x+c\). Jeśli \(f(3)=4\), to
A.\( f(1)=18 \)
B.\( f(1)=6 \)
C.\( f(1)=0 \)
D.\( f(1)=-6 \)
Wykres funkcji kwadratowej \(f\) danej wzorem \(f(x)=2x^2-5x+3\) przecięto prostymi o równaniach \(x=-1\) oraz \(x=2\). Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji \(f\).