Przesunięcia wykresów funkcji

Poziom podstawowy

Wykres dowolnej funkcji możemy przesuwać w poziomie oraz w pionie.
Wartości o jakie przesuwamy wykres w każdym z tych dwóch kierunków, najłatwiej jest zapisywać w postaci wektora przesunięcia:

Jeżeli chcemy przesunąć wykres w lewo, albo w dół, to na współrzędnych wektora podamy liczby ujemne, np.:

Wektor \(\vec{v}=[5,0]\) oznacza przesunięcie o \(5\) jednostek w prawo.
Wektor \(\vec{v}=[-7,0]\) oznacza przesunięcie o \(7\) jednostek w lewo.
Wektor \(\vec{v}=[0,6]\) oznacza przesunięcie o \(6\) jednostek w górę.
Wektor \(\vec{v}=[0,-6]\) oznacza przesunięcie o \(6\) jednostek w dół.
Wektor \(\vec{v}=[9,12]\) oznacza przesunięcie o \(9\) jednostek w prawo i \(12\) jednostek do góry.
Wektor \(\vec{v}=[-2,3]\) oznacza przesunięcie o \(2\) jednostki w lewo i \(3\) jednostki do góry.
Wektor \(\vec{v}=[-3,-4]\) oznacza przesunięcie o \(3\) jednostki w lewo i \(4\) jednostki do dołu.
Wektor \(\vec{v}=[1,-2]\) oznacza przesunięcie o \(1\) jednostkę w prawo i \(2\) jednostki do dołu.

Jak zmienia się wzór funkcji po przesunięciu o wektor?

Gdy przesuwamy wykres funkcji o wektor \(\vec{v}=[p,q]\), to:

we wzorze funkcji zamieniamy każdego \(x\) na wyrażenie \((x - p)\),
do całego wzoru funkcji dodajemy liczbę \(q\).

Czyli jeśli przesuniemy funkcję \(f(x)\) o wektor \(\vec{v}=[p,q]\) to otrzymamy funkcję: \[g(x)=f(x-p)+q\]

Zapisz wzór funkcji \(g(x)\), która powstaje przez przesunięcie funkcji \(f(x) = x^2\) o wektor \(\vec{v} = [3, 5]\).

We wzorze funkcji \(f(x)\) zamieniamy \(x\) na wyrażenie \((x-3)\) i do całego wzoru dodajemy \(5\): \[g(x)=(x-3)^2+5\] Całe przesunięcie o wektor \(\vec{v} = [3, 5]\) można podzielić najpierw na przesunięcie w poziomie:

a następnie w pionie:

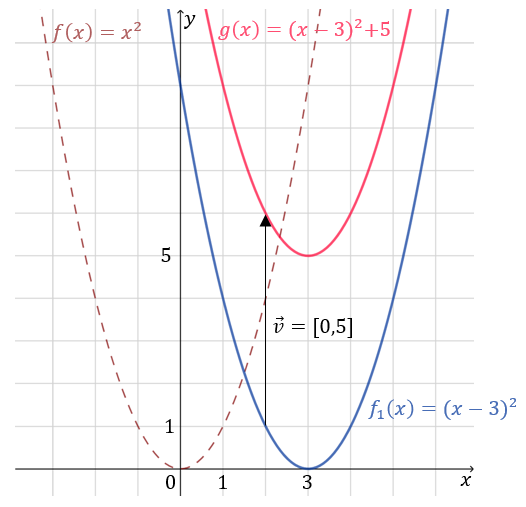Przesunięcie od razu o cały wektor \(\vec{v} = [3, 5]\) ilustruje rysunek:

Zapisz wzór funkcji \(g(x)\), która powstaje przez przesunięcie funkcji \(f(x) = x^2\) o wektor \(\vec{v} = [-2, 1]\).

We wzorze funkcji \(f(x)\) zamieniamy \(x\) na wyrażenie \((x-(-2))\) (czyli na wyrażenie \((x+2)\)) i do całego wzoru dodajemy \(1\): \[g(x)=(x+2)^2+1\] Całe przesunięcie ilustruje rysunek: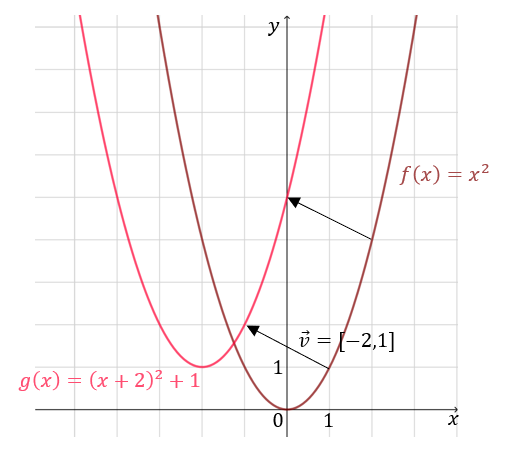

Zapisz wzór funkcji \(g(x)\), która powstaje przez przesunięcie funkcji \(f(x) = 5x^2 - 3x - 2\) o wektor \(\vec{v} = [7, 6]\).

We wzorze funkcji \(f(x)\) zamieniamy każdego \(x\) przez wyrażenie \((x - 7)\) i do całego wzoru dodajemy liczbę \(6\): \[g(x) = 5(x - 7)^2 - 3(x - 7) - 2+6\] Na koniec przekształcamy wzór do najprostszej postaci: \[ \begin{split} g(x) &= 5(x - 7)^2 - 3(x - 7) - 2+6\\[6pt] g(x) &= 5(x^2-14x+49)-3x+21+4\\[6pt] g(x) &= 5x^2-70x+245-3x+25\\[6pt] g(x) &= 5x^2-73x+270\\[6pt] \end{split} \]

Funkcję \(f(x)\) przesunięto wzdłuż osi układu współrzędnych, otrzymując funkcję o wzorze \(g(x)=f(x+4)\). Wobec tego funkcję \(f(x)\) przesunięto o:

A.\( 4 \) jednostki w prawo

B.\( 4 \) jednostki w górę

C.\( 4 \) jednostki w lewo

D.\( 4 \) jednostki w dół

Funkcja liniowa \(f\) jest określona wzorem \(f(x)=-2x+4\). Wykres funkcji \(f\) przesunięto wzdłuż osi \(Ox\) o \(2\) jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji \(g\). Funkcja \(g\) jest określona wzorem

A.\( g(x)=-2x+2 \)

B.\( g(x)=-2x \)

C.\( g(x)=-2x+6 \)

D.\( g(x)=-2x+8 \)

Gdy przesuniemy wykres funkcji \(f(x)=2x-3\) o \(2\) jednostki w prawo i \(4\) jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem

A.\( y=2(x-2)+4 \)

B.\( y=2(x-2)-4 \)

C.\( y=2(x-2)+1 \)

D.\( y=2(x+2)+4 \)

Na rysunku 1 przedstawiony jest wykres funkcji \(y=f(x)\) określonej dla \(x\in [-7, 4]\).

Rysunek 2 przedstawia wykres funkcji

A.\( y=f(x+2) \)

B.\( y=f(x)-2 \)

C.\( y=f(x-2) \)

D.\( y=f(x)+2 \)

Rysunek przedstawia wykres funkcji \(y = f(x)\).

Wskaż rysunek na którym jest przedstawiony wykres funkcji \(y = f(x + 1)\).

Na rysunku 1. jest przedstawiony wykres funkcji \(y=f(x)\)

Funkcja przedstawiona na rysunku 2. określona jest wzorem

A.\( y=f(x)+2 \)

B.\( y=f(x)-2 \)

C.\( y=f(x-2) \)

D.\( y=f(x+2) \)

Funkcję \(f(x)=7x-5\) przesunięto o wektor \(\vec{v} = [0; -3]\) otrzymując funkcję \(g(x)\). Funkcja \(g(x)\) określona jest wzorem

A.\( g(x)=7x-8 \)

B.\( g(x)=7x-2 \)

C.\( g(x)=7x-26 \)

D.\( g(x)=7x+19 \)

Funkcję \(f(x)=7x-5\) przesunięto o wektor \(\vec{v}=[5; 1]\) otrzymując funkcję \(g(x)\). Funkcja \(g(x)\) określona jest wzorem

A.\( g(x)=7x-1 \)

B.\( g(x)=7x+1 \)

C.\( g(x)=7x-39 \)

D.\( g(x)=7x-41 \)

Funkcja \(g\) jest określona wzorem

A.\( g(x)=f(x-1) \)

B.\( g(x)=f(x)-1 \)

C.\( g(x)=f(x+1) \)

D.\( g(x)=f(x)+1 \)

Wierzchołek paraboli będącej wykresem funkcji kwadratowej \(y = f (x)\) ma współrzędne \((2, 2)\). Wówczas wierzchołek paraboli będącej wykresem funkcji \(g(x) = f(x + 2)\) ma współrzędne

A.\( (4,2) \)

B.\( (0,2) \)

C.\( (2,0) \)

D.\( (2,4) \)

Wykres funkcji \(f(x)=-3^x\) przesunięto równolegle wzdłuż osi \(OX\) o dwie jednostki w prawo i otrzymano wykres funkcji \(y=g(x)\). Wówczas:

A.\( g(x)=-3^x+2 \)

B.\( g(x)=-3^{x+2} \)

C.\( g(x)=-3^x-2 \)

D.\( g(x)=-3^{x-2} \)

Na rysunku przedstawiono fragment wykresu funkcji \( f \), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \( y=\frac{1}{x} \) dla każdej liczby rzeczywistej \( x\ne 0 \).

a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \( f \) są większe od \( 0 \).
b) Podaj miejsce zerowe funkcji \( g \) określonej wzorem \( g(x)=f(x-3) \).

a) \(x\in (2;3)\)
b) \(x=6\)