Wektory w układzie współrzędnych
Poziom podstawowy
Definicja
Wektor - to odcinek z wyróżnionym początkiem i końcem (strzałka).Wektor o początku \(A\) i końcu \(B\) oznaczamy: \(\overrightarrow{A B}\).
Wektor o określonym początku i końcu nazywamy czasem wektorem zaczepionym.
Współrzędne wektora zapisujemy w nawiasach kwadratowych. Dla wektora z rysunku powyżej mamy: \[\overrightarrow{AB}=[3,4]\] Pierwsza współrzędna oznacza przesunięcie wzdłuż osi \(Ox\), a druga wzdłuż osi \(Oy\).
Wektora \(\overrightarrow{AB}=[p,q]\) oznacza przesunięcie wzdłuż osi \(x\)-ów o \(p\) jednostek, a wzdłuż osi \(y\)-ów o \(q\) jednostek.
- Jeżeli \(p\gt 0\), to przesunięcie jest w prawo, a jeżeli \(p\lt 0\), to przesunięcie jest w lewo.
- Jeżeli \(q\gt 0\), to przesunięcie jest do góry, a jeżeli \(q\lt 0\), to przesunięcie jest w dół.
Jeżeli dane są punkty \(A=(x_1,y_1)\) oraz \(B=(x_2,y_2)\), to współrzędne wektora \(\overrightarrow{AB}\) określa wzór: \[\overrightarrow{AB}=[x_2-x_1,y_2-y_1]\]
Narysuj wektor o początku w punkcie \(A=(2,1)\) i końcu w punkcie \(B=(5,6)\). Oblicz współrzędne tego wektora.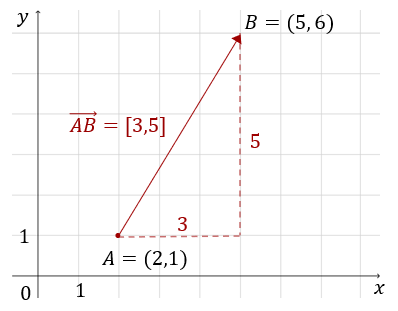 
\[\overrightarrow{AB}=[5-2,\ 6-1]=[3,5]\] Wektor o przeciwnym zwrocie, czyli \(\overrightarrow{BA}\) wygląda tak: 
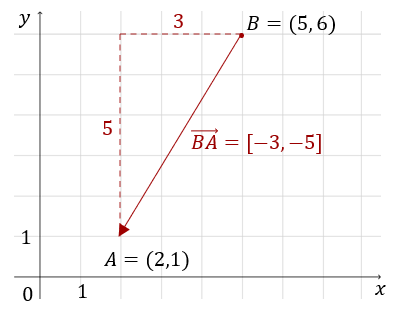i ma takie współrzędne: \[\overrightarrow{AB}=[2-5,\ 1-6]=[-3,-5]\]
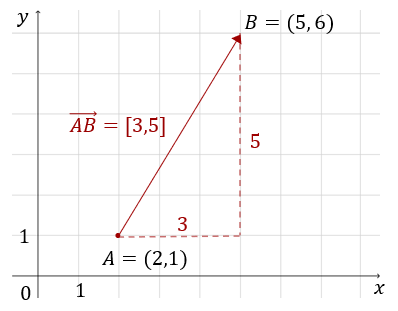\[\overrightarrow{AB}=[5-2,\ 6-1]=[3,5]\] Wektor o przeciwnym zwrocie, czyli \(\overrightarrow{BA}\) wygląda tak: 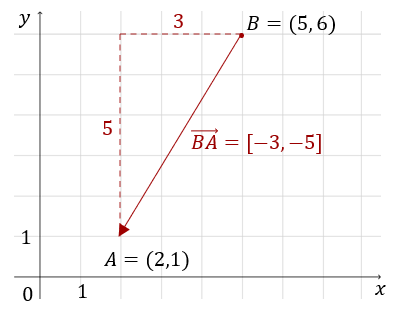i ma takie współrzędne: \[\overrightarrow{AB}=[2-5,\ 1-6]=[-3,-5]\] Wektor \(\overrightarrow{BA}\) nazywamy wektorem przeciwnym do wektora \(\overrightarrow{AB}\).
Jeżeli \(\overrightarrow{AB}=[p,q]\), to \(\overrightarrow{BA}=[-p,-q].\)
Jeżeli \(\overrightarrow{AB}=[p,q]\), to \(\overrightarrow{BA}=[-p,-q].\)
Narysuj wektor o początku w punkcie \(A=(1,5)\) i końcu w punkcie \(B=(8,2)\). Oblicz współrzędne tego wektora i wyznacz wektor do niego przeciwny.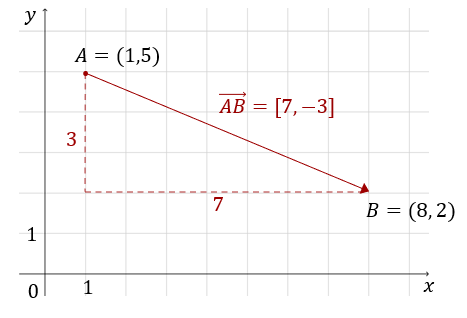 
\[\overrightarrow{AB}=[8-1,\ 2-5]=[7, -3]\] Wektor przeciwny do \(\overrightarrow{AB}\), czyli \(\overrightarrow{BA}\) wygląda tak: 
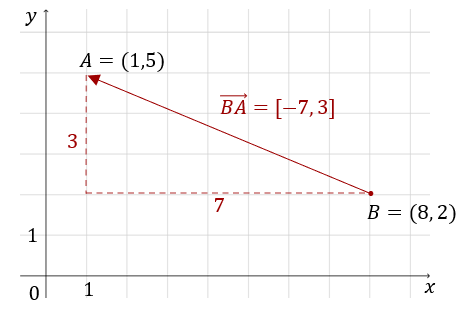i ma współrzędne: \[\overrightarrow{BA}=[1-8,\ 5-2]=[-7,3]\]
\[\overrightarrow{AB}=[8-1,\ 2-5]=[7, -3]\] Wektor przeciwny do \(\overrightarrow{AB}\), czyli \(\overrightarrow{BA}\) wygląda tak: i ma współrzędne: \[\overrightarrow{BA}=[1-8,\ 5-2]=[-7,3]\] Wyznacz współrzędne wektorów zaznaczonych na rysunku: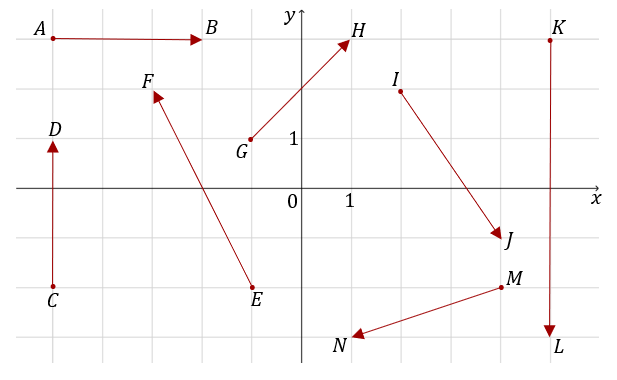 
\(\overrightarrow{AB}=[3,0]\),\(\quad \) \(\overrightarrow{CD}=[0,3]\),\(\quad \) \(\overrightarrow{EF}=[-2,4]\),\(\quad \) \(\overrightarrow{GH}=[2,2]\),\(\quad \) \(\overrightarrow{IJ}=[2,-3]\),\(\quad \) \(\overrightarrow{KL}=[0,-6]\),\(\quad \) \(\overrightarrow{MN}=[-3,-1]\).
Definicja
Wektor swobodny - to wektor dla którego podane są tylko współrzędne, a nie ma określonego początku i końca.Takie wektory oznaczamy zwykle: \(\overrightarrow{v}, \overrightarrow{u}, \overrightarrow{w}\).
Wszystkie wektory zaznaczone poniżej odpowiadają wektorowi swobodnemu \(\overrightarrow{v}=[3,1]\).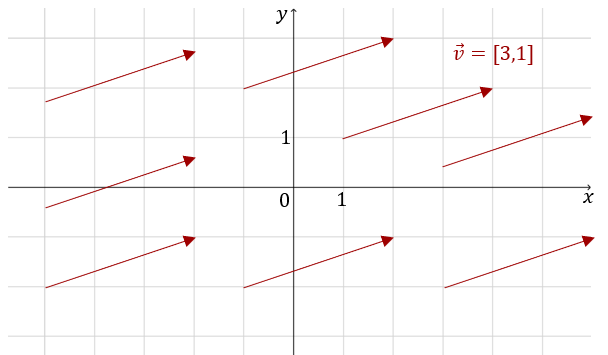 
O jaki wektor należy przesunąć trójkąt \(ABC\) aby otrzymać tróją \(A'B'C'\)?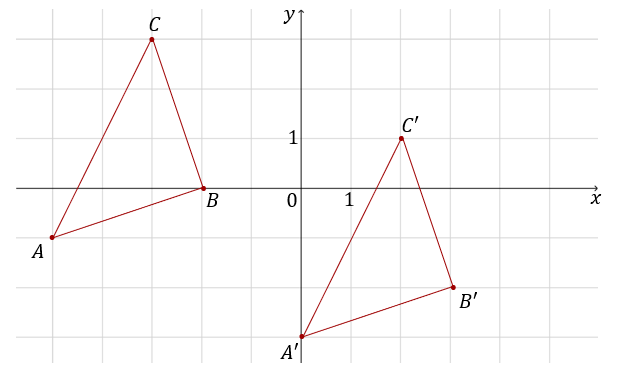 
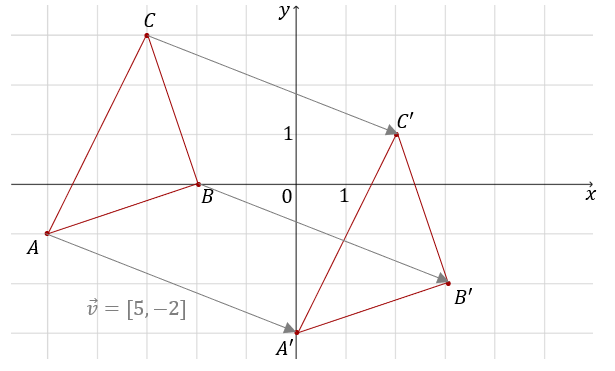Przesunięcie należy wykonać o wektor \(\overrightarrow{v}=[5,-2]\).
Przesunięcie należy wykonać o wektor \(\overrightarrow{v}=[5,-2]\). Wektory swobodne często wykorzystujemy do opisywania przesunięć figur i wykresów funkcji w układzie współrzędnych.
Tematy nadrzędne i sąsiednie