Przekształcanie wykresu przez symetrię względem osi układu współrzędnych
Poziom podstawowy
Jeżeli wykres funkcji \(y=f(x)\) odbijemy symetrycznie względem osi \(OX\), to otrzymamy wykres funkcji \(y=-f(x)\).
Zapisz wzór funkcji \(g(x)\), która powstaje przez symetryczne odbicie wykresu funkcji \(f(x)=x^2+1\) względem osi \(OX\).
\[g(x)=-f(x)=-(x^2+1)=-x^2-1\] Ilustracja obu funkcji: 
Zapisz wzór funkcji \(g(x)\), która powstaje przez symetryczne odbicie wykresu funkcji \(f(x)=2x-3\) względem osi \(OX\).
\[g(x)=-f(x)=-(2x-3)=-2x+3\] Ilustracja obu funkcji: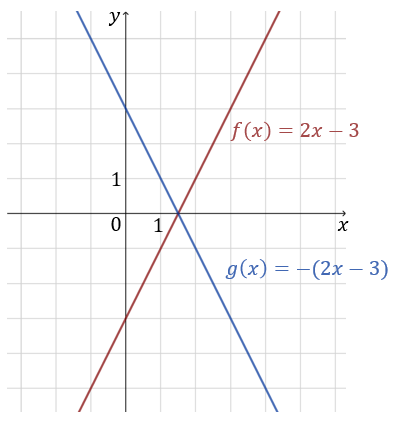 
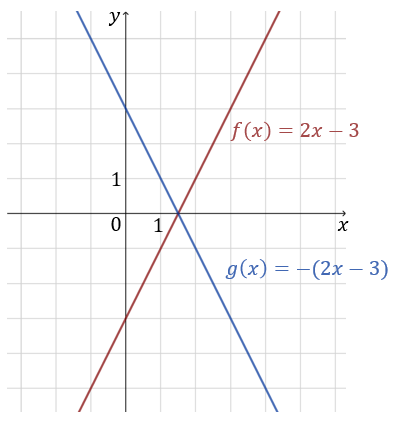
Jeżeli wykres funkcji \(y=f(x)\) odbijemy symetrycznie względem osi \(OY\), to otrzymamy wykres funkcji \(y=f(-x)\).
Zapisz wzór funkcji \(g(x)\), która powstaje przez symetryczne odbicie wykresu funkcji \(f(x)=2x-3\) względem osi \(OY\).
\[g(x)=f(-x)=2(-x)-3=-2x-3\] Ilustracja obu funkcji: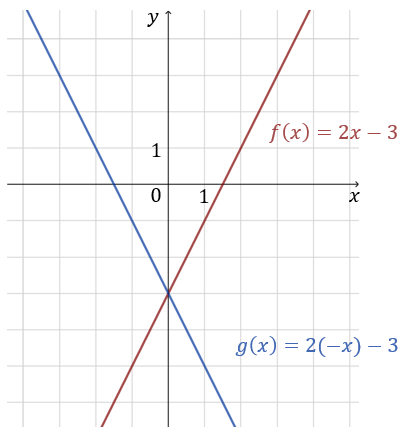 
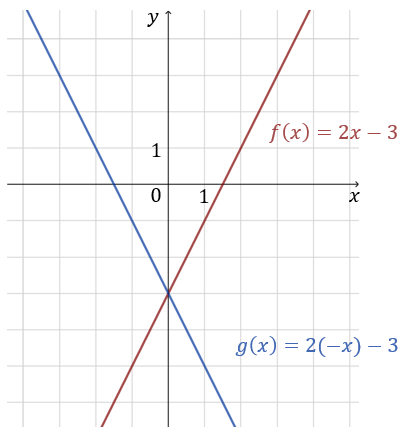
Zapisz wzór funkcji \(g(x)\), która powstaje przez symetryczne odbicie wykresu funkcji \(f(x)=x^2+1\) względem osi \(OY\).
Wykresem funkcji \(f(x)\) jest parabola, która jest symetryczna względem osi \(OY\). Zatem odbicie symetryczne względem osi \(OY\) nie zmieni wykresu i wzoru funkcji, co potwierdza rachunek: \[g(x)=f(-x)=(-x)^2+1=x^2+1\]
Jeżeli wykres funkcji \(y=f(x)\) odbijemy symetrycznie względem początku układu współrzędnych, to otrzymamy wykres funkcji \(y=-f(-x)\).
Takie odbicie jest złożeniem symetrii względem osi \(OX\) i osi \(OY\).
Takie odbicie jest złożeniem symetrii względem osi \(OX\) i osi \(OY\).
Zapisz wzór funkcji \(g(x)\), która powstaje przez symetryczne odbicie wykresu funkcji \(f(x)=(x-1)^2+2\) względem początku układu współrzędnych.
Wyznaczamy wzór funkcji \(g(x)\): 
\(g(x)=-f(-x)=-\Bigl((-x-1)^2+2\Bigl)\) \(=-\Bigl((x+1)^2+2\Bigl)=-(x+1)^2-2\)
Wzór funkcji, której wykres powstaje przez symetrię osiową względem osi \(OX\) wykresu funkcji \(f(x)=x^2-4\), to:
A.\( f(x)=(x+4)^2 \)
B.\( f(x)=-x^2-4\ \)
C.\( f(x)=-x^2+4\ \)
D.\( f(x)=(x-4)^2 \)
Na rysunku przedstawiony jest wykres funkcji \(f\). 
Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji \(f\) względem osi \(Oy\) układu współrzędnych.
Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji \(f\) względem osi \(Oy\) układu współrzędnych. A.\( y=f(x-4) \)
B.\( y=f(x)-4 \)
C.\( y=f(x+4) \)
D.\( y=f(x)+4 \)
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej \(f\), przy czym \(f(0)=-2\) i \(f(1)=0\). 
Wykres funkcji \(g\) jest symetryczny do wykresu funkcji \(f\) względem początku układu współrzędnych. Funkcja \(g\) jest określona wzorem
Wykres funkcji \(g\) jest symetryczny do wykresu funkcji \(f\) względem początku układu współrzędnych. Funkcja \(g\) jest określona wzorem A.\( g(x)=2x+2 \)
B.\( g(x)=2x-2 \)
C.\( g(x)=-2x+2 \)
D.\( g(x)=-2x-2 \)
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej \(f\). Na wykresie tej funkcji leżą punkty \(A = (0, 4)\) i \(B = (2, 2)\). 
Obrazem prostej \(AB\) w symetrii względem początku układu współrzędnych jest wykres funkcji \(g\) określonej wzorem
Obrazem prostej \(AB\) w symetrii względem początku układu współrzędnych jest wykres funkcji \(g\) określonej wzorem A.\( g(x) = x + 4 \)
B.\( g(x) = x - 4 \)
C.\( g(x) = -x - 4 \)
D.\( g(x) = -x + 4 \)
Wykres funkcji wykładniczej \(f(x)=2^x\) poddano czterem przekształceniom w następującej kolejności:
- Przesunięcie o wektor \(\vec{v}=[3,4]\).
- Symetria względem osi \(OX\).
- Przesunięcie o wektor \(\vec{v}=[0,-1]\).
- Symetria względem osi \(OY\).
Tematy nadrzędne i sąsiednie