Przekształcenia wykresu funkcji logarytmicznej
Poziom podstawowy
Jeżeli wykres funkcji \(y=\log_ax\) przesuniemy o wektor \([p,q] \), to otrzymamy wykres funkcji: \[f(x)=\log_a(x-p)+q\] Naszkicuj wykres funkcji \(f(x)=\log_2 x+3\).
Wykres funkcji \(f\) możemy otrzymać przez przesunięcie wykresu funkcji \(y=\log_2 x\) o \(3\) jednostki w górę, czyli o wektor \([0,3]\).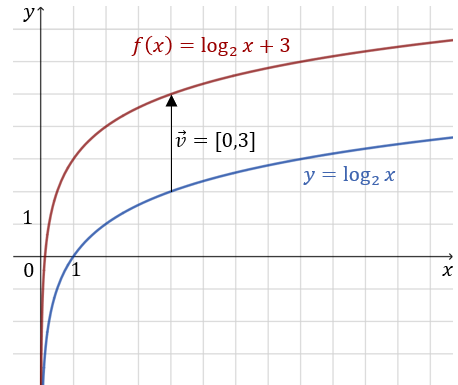 
Dziedziną funkcji \(f\) jest zbiór \(D_f=(0 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=0\).
Dziedziną funkcji \(f\) jest zbiór \(D_f=(0 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=0\). Naszkicuj wykres funkcji \(f(x)=\log_{\frac{1}{2}} x-3\).
Wykres funkcji \(f\) możemy otrzymać przez przesunięcie wykresu funkcji \(y=\log_{\frac{1}{2}} x\) o \(3\) jednostki w dół, czyli o wektor \([0,-3]\).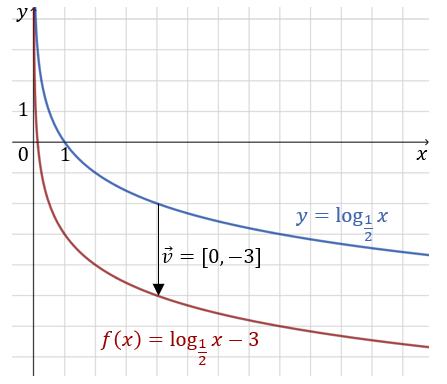 
Dziedziną funkcji \(f\) jest zbiór \(D_f=(0 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=0\).
Dziedziną funkcji \(f\) jest zbiór \(D_f=(0 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=0\). Naszkicuj wykres funkcji \(f(x)=\log_3 (x-2)\).
Wykres funkcji \(f\) możemy otrzymać przez przesunięcie wykresu funkcji \(y=\log_3 x\) o \(2\) jednostki w prawo, czyli o wektor \([2,0]\).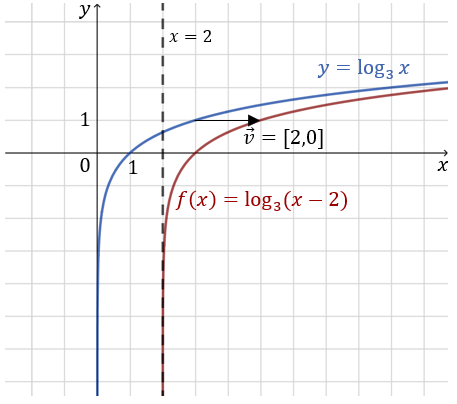 
Dziedziną funkcji \(f\) jest zbiór \(D_f=(2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=2\).
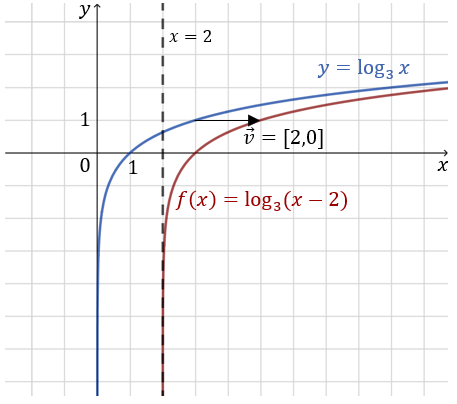Dziedziną funkcji \(f\) jest zbiór \(D_f=(2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=2\). Naszkicuj wykres funkcji \(f(x)=\log_3 (x+2)\).
Wykres funkcji \(f\) możemy otrzymać przez przesunięcie wykresu funkcji \(y=\log_3 x\) o \(2\) jednostki w lewo, czyli o wektor \([-2,0]\).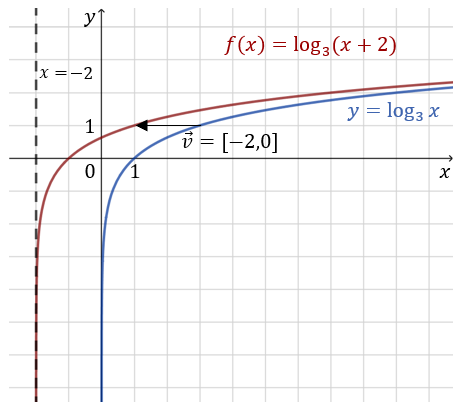 
Dziedziną funkcji \(f\) jest zbiór \(D_f=(-2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=-2\).
Dziedziną funkcji \(f\) jest zbiór \(D_f=(-2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=-2\). Poziom rozszerzony
Naszkicuj wykres funkcji \(f(x)=|\log_3 (x-2)|\).
Najpierw rysujemy wykres funkcji \(y=\log_3 (x-2)\) tak jak w przykładzie 3. Następnie odbijamy nad oś \(x\)-ów tę część wykresu, która przyjmuje wartości ujemne.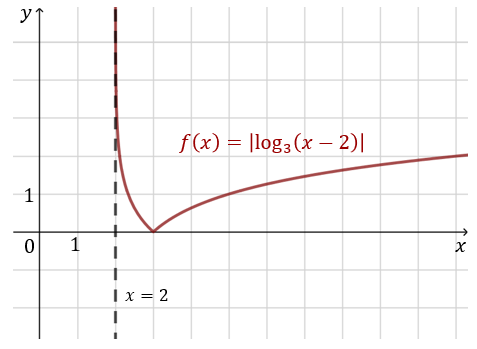 
Dziedziną funkcji \(f\) jest zbiór \(D_f=(2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=2\).
Zbiorem wartości funkcji \(f\) jest zbiór \(ZW_f=\langle 0 ; \infty)\).
Dziedziną funkcji \(f\) jest zbiór \(D_f=(2 ; \infty)\). Asymptotą pionową wykresu jest prosta \(x=2\).Zbiorem wartości funkcji \(f\) jest zbiór \(ZW_f=\langle 0 ; \infty)\).
Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej \(f\) określonej wzorem \(f(x)=\log_2 (x-p)\). 
a) Podaj wartość \(p\).
b) Narysuj wykres funkcji określonej wzorem \(y = |f(x)|\).
c) Podaj wszystkie wartości parametru \(m\), dla których równanie \(|f(x)| = m\) ma dwa rozwiązania o przeciwnych znakach.
a) Podaj wartość \(p\).b) Narysuj wykres funkcji określonej wzorem \(y = |f(x)|\).
c) Podaj wszystkie wartości parametru \(m\), dla których równanie \(|f(x)| = m\) ma dwa rozwiązania o przeciwnych znakach.
Tematy nadrzędne i sąsiednie