Porównywanie ułamków

Drukuj

Szkoła podstawowa

Jeżeli dwa ułamki mają równe mianowniki, to większy jest ten, który ma większy licznik.

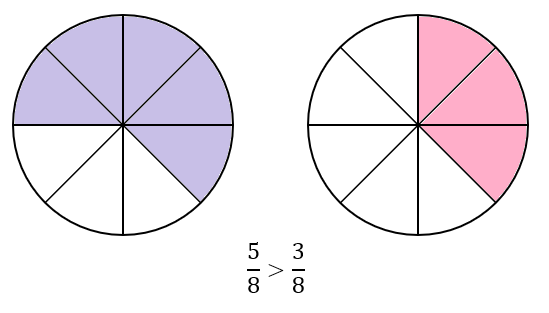
Jeżeli dwa ułamki mają równe liczniki, to większy jest ten, który ma mniejszy mianownik.

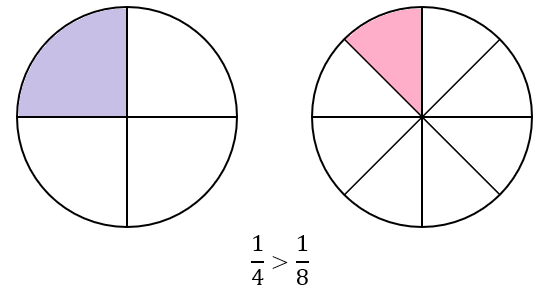
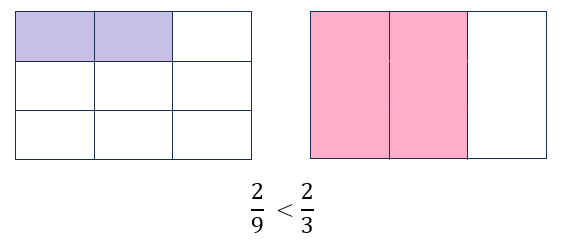
Zapisz ułamki w kolejności od najmniejszego do największego.

\(\frac{1}{5}, \frac{4}{5}, \frac{2}{5}\)

\(\frac{6}{8}, \frac{4}{8}, \frac{3}{8}\)

\(\frac{1}{10}, \frac{1}{1000}, \frac{1}{100}\)

\(\frac{2}{5}, \frac{2}{6}, \frac{2}{7}\)

\(\frac{1}{5} \lt \frac{2}{5} \lt \frac{4}{5}\)

\(\frac{3}{8} \lt \frac{4}{8} \lt \frac{6}{8}\)

\(\frac{1}{1000} \lt \frac{1}{100} \lt \frac{1}{10}\)

\(\frac{2}{7} \lt \frac{2}{6} \lt \frac{2}{5}\)

Jeżeli dwa ułamki mają różne mianowniki i liczniki, to żeby je porównać, należy najpierw sprowadzić je do wspólnego mianownika.

Który z ułamków \(\frac{2}{5}\) czy \(\frac{3}{7}\) jest większy?

Sprowadzamy ułamki do wspólnego mianownika: \[\frac{2}{5}=\frac{2\cdot 7}{5\cdot 7}=\frac{14}{35}\] \[\frac{3}{7}=\frac{3\cdot 5}{7\cdot 5}=\frac{15}{35}\] Zatem mamy: \[\frac{15}{35} \gt \frac{14}{35}\] Czyli: \[\frac{3}{7} \gt \frac{2}{5}\]