Okrąg opisany na trójkącie prostokątnym

Drukuj

Poziom podstawowy

Przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu opisanego na tym trójkącie.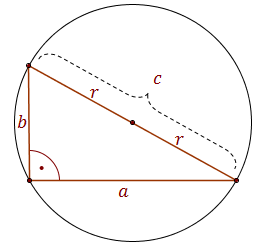

Środek okręgu opisanego leży na środku przeciwprostokątnej.
Długość przeciwprostokątnej można obliczyć ze wzoru: \[c=2r\]

W tym nagraniu wideo omawiam zależność między promieniem okręgu wpisanego i opisanego na trójkącie prostokątnym, a bokami trójkąta.

Dany jest trójkąt prostokątny o przyprostokątnych \(5\) i \(12\). Promień okręgu opisanego na tym trójkącie jest równy

A.\( 12 \)

B.\( 8{,}5 \)

C.\( 6{,}5 \)

D.\( 5 \)

Promień okręgu opisanego na trójkącie prostokątnym jest równy \(2\sqrt{5}\). Jedna z przyprostokątnych tego trójkąta jest o \(4\) dłuższa od drugiej przyprostokątnej. Oblicz wysokość tego trójkąta opuszczoną na przeciwprostokątną.

\(h=\frac{8\sqrt{5}}{5}\)