Najnowsze filmy
Na tej stronie umieszczam moje najnowsze filmy.
Dany jest trapez o podstawach \(a\) i \(b\) opisany na okręgu o promieniu \(r\). Wykaż, że \(4r^2 \leq ab\). 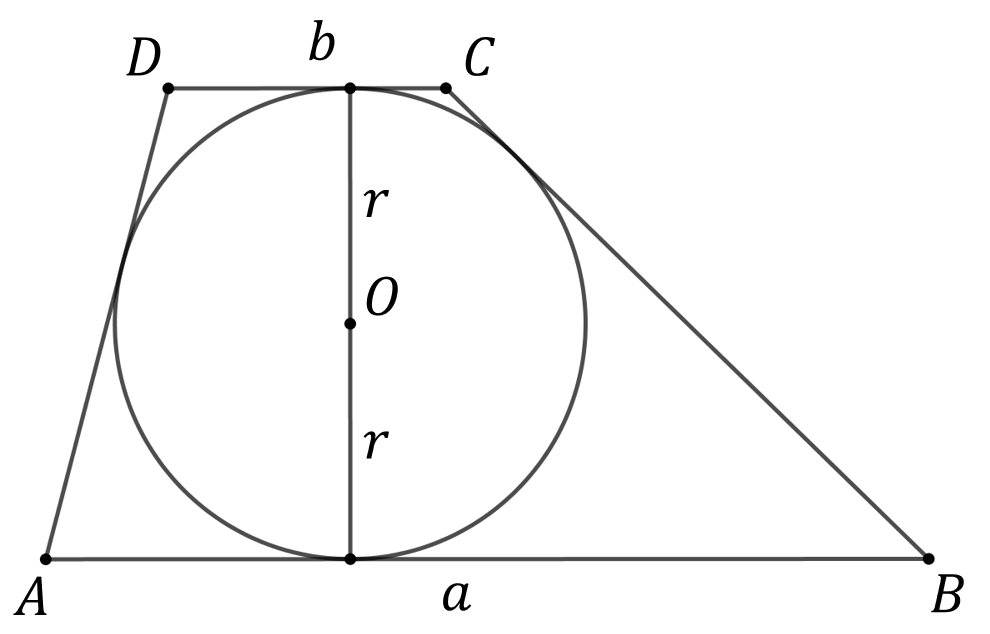

Oblicz pole wycinka koła o promieniu \(1\), wyznaczonego przez łuk o długości \(1\). 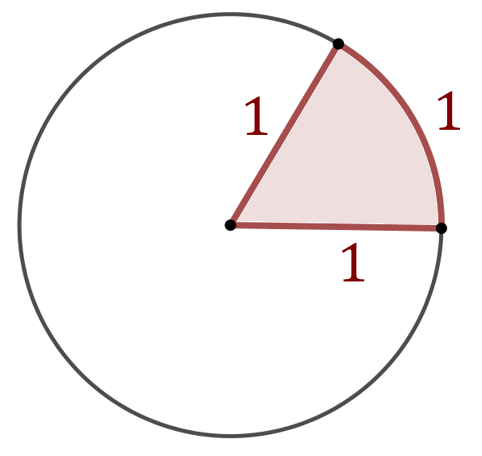

W trójkącie ostrokątnym \(ABC\) miara kąta \(BAC\) jest dwa razy większa od miary kąta \(ABC\). Punkt \(D\) jest środkiem boku \(AB\). Niech \(\alpha\) oznacza miarę kąta \(ABC\), natomiast \(\beta\)-miarę kąta \(ADC\) (zobacz rysunek). 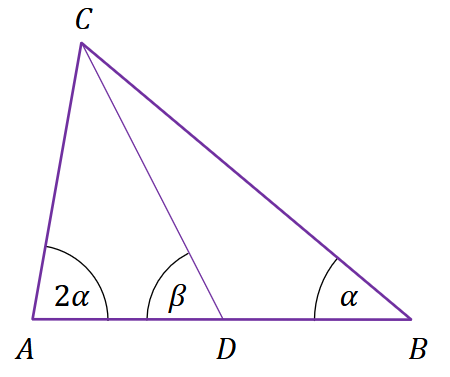

Oblicz \(\frac{\operatorname{tg} \beta}{\sin (2 \alpha)}\). Zapisz obliczenia.
Trzeci i piąty wyraz malejącego ciągu arytmetycznego \((a_{n})\), określonego dla każdej liczby naturalnej \(n \geq 1\), spełniają warunek \(a_{3}+a_{5}=10\).
Trzywyrazowy ciąg ( \(2 a_{1}+4, a_{4}-1,-\frac{1}{8} a_{7}\) ) jest geometryczny.
Trzywyrazowy ciąg ( \(2 a_{1}+4, a_{4}-1,-\frac{1}{8} a_{7}\) ) jest geometryczny.
Oblicz wyrazy tego ciągu geometrycznego. Zapisz obliczenia.
Funkcja kwadratowa \(f\) zmiennej rzeczywistej \(x\) jest określona wzorem \[ f(x)=x^{2}-3 x-m^{2}+m+3 \]
Wyznacz wszystkie wartości parametru \(m\), dla których funkcja \(f\) ma dwa różne miejsca zerowe \(x_{1}, x_{2}\) spełniające warunek \(\left|x_{1}^{2}-x_{2}^{2}\right| \leq 12\). Zapisz obliczenia.
Oblicz granicę \[ \lim _{n \rightarrow+\infty} \frac{1+3+5+7+\ldots+(2 n+1)}{\binom{n}{2}} \] gdzie \(1+3+5+7+\ldots+(2 n+1)\) jest sumą kolejnych liczb naturalnych nieparzystych.
Rozwiąż równanie \[ \sin ^{4} x=\sin x \cdot \cos x-\cos ^{4} x \] w zbiorze \([-\pi, 2 \pi]\). Zapisz obliczenia.
Rozwiąż równanie \[ |4x-8|+|x-2|=|2-x|+|x+2|+4 \]
W kartezjańskim układzie współrzędnych \((x, y)\) dane są:
okrąg o równaniu \((x+1)^{2}+(y-3)^{2}=50\) i punkty \(A=(6,4)\) oraz \(B=(-6,8)\).
Punkt \(C\) leży na tym okręgu i \(|A C|=|B C|\).
okrąg o równaniu \((x+1)^{2}+(y-3)^{2}=50\) i punkty \(A=(6,4)\) oraz \(B=(-6,8)\).
Punkt \(C\) leży na tym okręgu i \(|A C|=|B C|\).
Oblicz współrzędne punktu \(C\). Rozważ wszystkie przypadki. Zapisz obliczenia.
Wykaż, że \[ \frac{1}{\log _{2} 35+1}+\frac{1}{\log _{7} 140-\log _{7} 2}+\frac{1}{\log _{5} 7+\log _{5} 2+1}=1 \]
W pewnej lokalnej społeczności \(35 \%\) osób ma wyższe wykształcenie. W tej społeczności językiem niemieckim dobrze włada \(70 \%\) osób mających wyższe wykształcenie i \(40 \%\) osób bez wyższego wykształcenia.
Spośród członków tej społeczności wybieramy losowo jedną osobę.
Spośród członków tej społeczności wybieramy losowo jedną osobę.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wybierzemy osobę z wyższym wykształceniem, jeżeli wiadomo, że ta osoba dobrze włada językiem niemieckim. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych. Zapisz obliczenia.
Iloczyn długości średnicy podstawy walca i wysokości walca jest równy \(12 \sqrt{3}\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).
Pole powierzchni całkowitej tego walca jest równe \(12 \pi(\sqrt{3}+1)\).
Oblicz objętość tego walca. Zapisz obliczenia.
Okrąg \(\mathcal{O}\) jest styczny do boków \(A C\) i \(B C\) trójkąta \(A B C\) oraz przecina bok \(A B\) tego trójkąta w punktach \(M\) oraz \(N\), przy czym \(0\lt |A M|\lt |A N|\lt |A B|\).
Wykaż, że jeśli \(|A M|=|B N|\), to trójkąt \(A B C\) jest równoramienny.
Ładunek elektryczny zgromadzony w kondensatorze można opisać zależnością \[ Q(t)=Q_{0} \cdot \beta^{-t} \quad \text { dla } \quad t \geq 0 \] gdzie:
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.
\(Q_{0}\) - ładunek elektryczny zgromadzony w kondensatorze w chwili początkowej \((t=0)\) wyrażony w milikulombach
\(Q\) - ładunek elektryczny zgromadzony w kondensatorze w chwili \(t\) (licząc od chwili początkowej) wyrażony w milikulombach
\(\beta\) - stała dodatnia
\(t\) - czas wyrażony w sekundach.
Wiadomo, że w chwili \(t=4 \mathrm{~s}\) w kondensatorze był zgromadzony ładunek \(2\) milikulombów, a w chwili \(t=6 \mathrm{~s}\) - ładunek \(18\) milikulombów.
Oblicz, ile milikulombów ładunku było zgromadzone w tym kondensatorze w chwili \(t=5 \mathrm{~s}\). Zapisz obliczenia.
Wykaż, że dla dowolnych dodatnich liczb \(a, b, c \gt 0\) i \(b\ne1\), takich, że, \(b\ne 1\) zachodzi równość: \[a^{\large{\log_bc}}=c^{\large{\log_ba}}\]
W tej lekcji pokazuję na trzech przykładach jak można radzić sobie z modułami w warunkach na rozwiązania równania kwadratowego.
Zadanie 1.
Dla jakich wartości parametru \(m\) różne rozwiązania \(x_1, x_2\) równania \(x^2+2 x+m-1=0\) spełniają warunek \(\left|x_1\right|+\left|x_2\right| \leq 3\) ? Zadanie 2.
Dla jakich wartości parametru \(m, m \in R\), różne rozwiązania \(x_1, x_2\) równania \(-x^2+x+m-4=0\) spełniają warunek \(\left|x_1\right|+\left|x_2\right|>2\) ? Zadanie 3.
Dla jakich wartości parametru \(m, m \in R\), różne rozwiązania \(x_1, x_2\) równania \(5 x^2-m x+1=0\) spełniają warunek \(\left|x_1-x_2\right| \geq 1\) ?Wzory Viete'a
Jeżeli równanie \(ax^2+bx+c=0\) ma dwa rozwiązania \(x_1\) i \(x_2\) to: \[x_1+x_2=-\frac{b}{a} \] \[x_1 \cdot x_2=\frac{c}{a}\]Zadanie 1. (6 x 6 pkt)
Wyznacz wszystkie wartości parametru \(m\) dla których równanie \((m^2-4)x^2-(2m+3)x+1=0\) ma dwa rozwiązania: - dodatnie.
- ujemne.
- jednakowych znaków.
- różnych znaków.
- jedno mniejsze od \(2\), a drugie większe od \(2\).
- spełniające warunek: \(x_1^2-x_1x_2+x_2^2\leqslant \frac{12m+26}{m^4-8m^2+16}\).
Zadanie 2. (5 pkt)
Wyznacz wszystkie wartości parametru \(m\) dla których równanie \(x^2+2(m-1)x+m^2-4=0\) ma dwa rozwiązania \(x_1\) oraz \(x_2\) spełniające warunek: \(x_1^2+x_2^2\leqslant 12\). Ćwiczenie na wzory Viete'a
Zapisz za pomocą wyrażeń \(x_1+x_2\) oraz \(x_1\cdot x_2\): - \(\frac{1}{x_1^2}+\frac{1}{x_2^2}\)
- \((x_1-x_2)^2\)
- \((x_1+5x_2)(x_2+5x_1)\)
- \(x_1x_2^2+x_1^2x_2\)
- \(x_1^3+x_2^3\)
- \((|x_1|+|x_2|)^2\)
.Promień dużego koła wynosi \(2\). Oblicz pole zamalowanego koła. 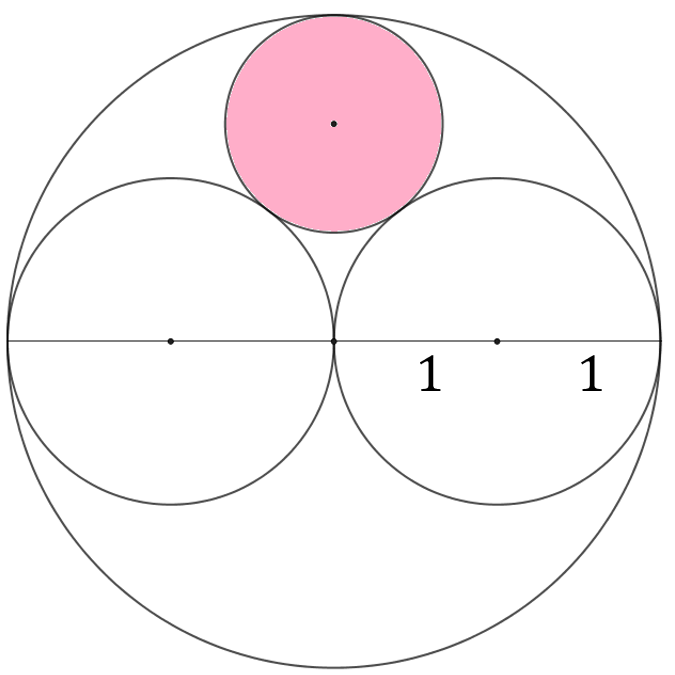

Na filmie pokazuję jak za pomocą dwóch funkcji matematycznych można wygenerować serce. 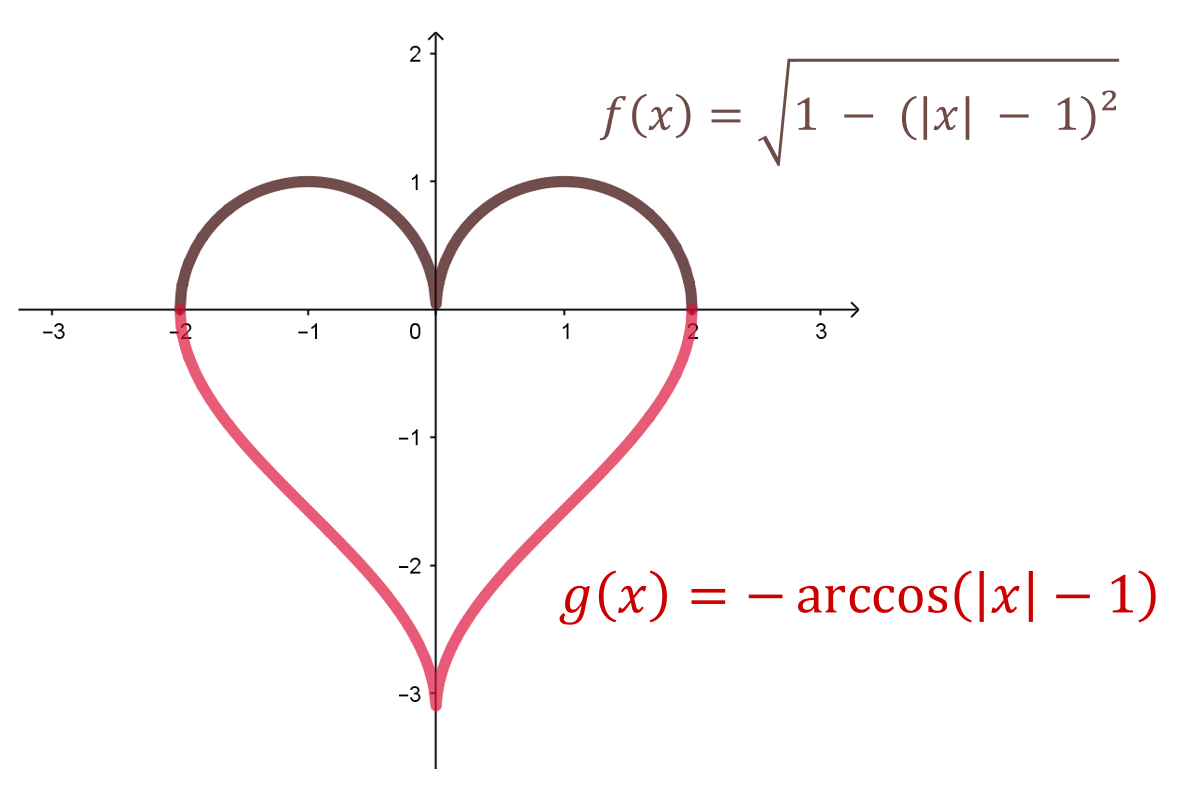
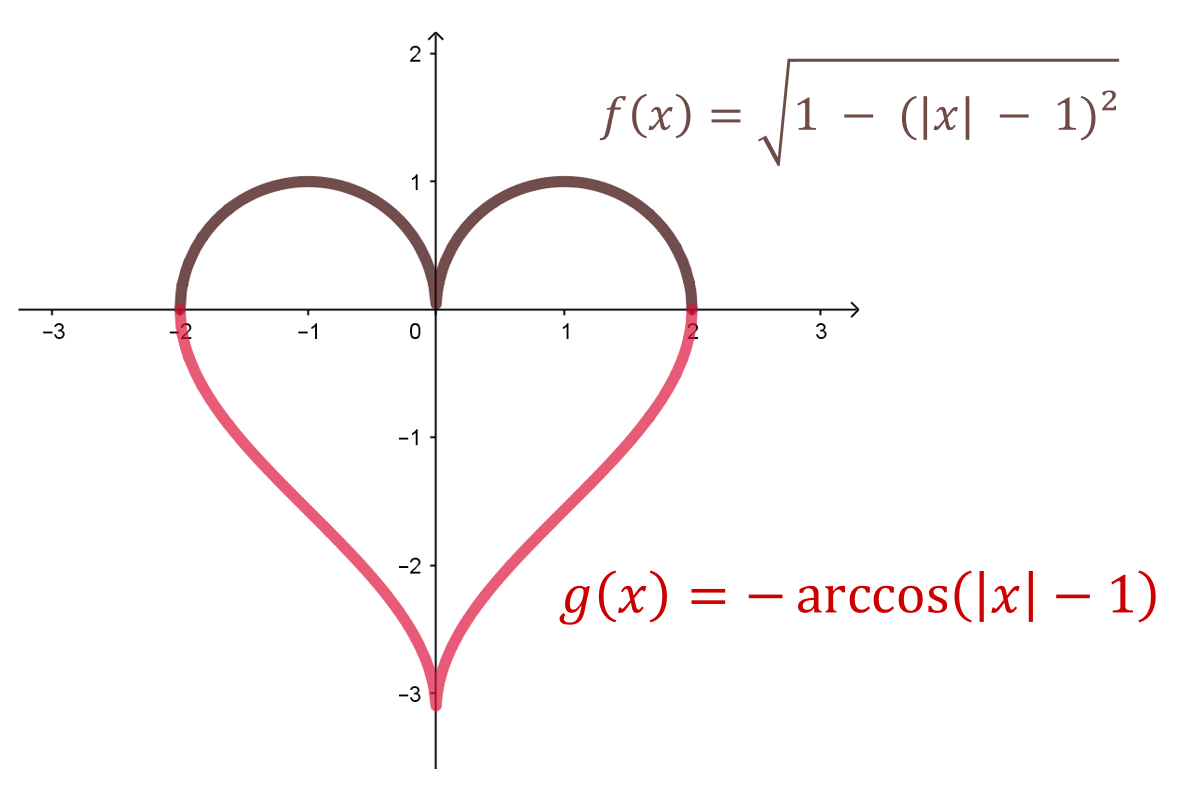
Wyznacz wszystkie parametry \(m\) dla których równanie \[x^2-10mx=6-25m^2-2m\] ma:
- dwa różne rozwiązania dodatnie.
- dwa różne rozwiązania większe od \(3\).
Dla jakich wartości parametru \(k \in R\), funkcja kwadratowa \(f(x)=x^2-2 x+k\) ma dwa miejsca zerowe \(x_1, x_2\) spełniające warunek: \(7 x_2-4 x_1=47\) ?
W tym materiale omawiam wszystkie najważniejsze wiadomości dotyczące potęg wymagane na egzaminie ósmoklasisty. Poniżej znajdują się ćwiczenia z lekcji, a na samym dole jest film z omówieniem tych przykładów.
Definicja Potęgi
\[a^n=\underbrace{a\cdot a\cdot a\cdot...\cdot a}_{n \text{ razy}}\]Ćwiczenie 1.
Oblicz potęgi: \(3^2\), \(3^3\), \(3^4\), \(7^1\), \(7^0\). Ćwiczenie 2.
Zapisz w postaci potęgi, a następnie oblicz: - czwartą potęgę liczby \(5\),
- siódmą potęgę liczby \(\frac{1}{2}\),
- potęgę o podstawie \(-4\) i wykładniku \(3\).
- potęgę o podstawie \(-1,1\) i wykładniku \(2\).
- potęgę o podstawie \(\frac{1}{3}\) i wykładniku \(5\).
Ćwiczenie 3.
Oblicz: - \((-3)^4=\)
- \(-3^4=\)
- \(\left(-2\frac{1}{2}\right)^2=\)
- \(\left(1\frac{7}{6}\right)^0=\)
- \(10^5=\)
- \((0,1)^5=\)
Potęgi o tych samych podstawach
\[a^m\cdot a^n=a^{m+n}\] \[a^m\cdot a^n=\underbrace{\underbrace{a\cdot a\cdot ...\cdot a}_{m \text{ razy}}\cdot \underbrace{a\cdot a\cdot ...\cdot a}_{n \text{ razy}}}_{m+n \text{ razy}}=a^{m+n}\] \[a^m:a^n=\frac{a^m}{a^n}=a^{m-n}\]Ćwiczenie 4.
Zapisz w postaci jednej potęgi: - \(2^3\cdot 2^4=\)
- \(3^5\cdot 3^6=\)
- \(\left(\frac{2}{7}\right)^{10}\cdot \left(\frac{2}{7}\right)^8=\)
- \(7^5 : 7^2=\)
- \(10^8:10^{5}=\)
Podnoszenie potęgi do potęgi
\[{\bigl(a^m\bigl)}^n=a^{m\cdot n}\]Ćwiczenie 5.
Zapisz w postaci potęgi: - \(\bigl(2^3\bigl)^4=\)
- \(\bigl(3^5\bigl)^7=\)
- \(\bigl((-5)^3\bigl)^6=\)
- \(\bigl(17^{19}\bigl)^3:17^{55}=\)
- \(\frac{\bigl((-2)^3\bigl)^5\cdot (-2)^6}{\bigl((-2)^2\bigl)^2}=\)
Potęgi o tych samych wykładnikach
\[ a^n\cdot b^n=(a\cdot b)^n \] \[a^n:b^n=\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n\]Ćwiczenie 6.
Zapisz w postaci potęgi: - \(2^5\cdot 3^5=\)
- \(8^7\cdot \left(\frac{1}{4}\right)^7=\)
- \(10^{15}:5^{15}=\)
- \(\frac{9^7}{3^7}=\)
Ćwiczenie 7.
Zapisz w postaci potęgi: - \(4^5\cdot 7^{10}=\)
- \(8^7\cdot \left(\frac{1}{3}\right)^{21}=\)
- \(25^{12}:27^{8}=\)
- \(\frac{3^8\cdot 6^8}{4^4}=\)
Ćwiczenie 8.
Zapisz w postaci potęgi: - \((5^7:5^4\cdot 5^5):(5^{10}\cdot 5^0)=\)
- \(\frac{(7^2\cdot 7^0)^3}{7\cdot 7^2:(49^{6}:7^{11})}=\)
- \(\frac{100^8:4^8}{5^{12}}=\)
- \(36^{11}\cdot \left(\frac{1}{3}\right)^{22}:2^9=\)
Notacja wykładnicza
\[a\cdot 10^n\] gdzie:\(a\) - to liczba rzeczywista z przedziału \(\langle 1,10)\),
\(n\) - to liczba całkowita.
Ćwiczenie 9.
Zapisz w postaci wykładniczej: - \(800=\)
- \(13\ 000=\)
- \(171\ 000\ 000=\)
- \(0,00001=\)
- \(0,00023=\)
- \(0,0000723=\)
Ćwiczenie 10.
Zapisz w postaci wykładniczej: - \(7\cdot 10^{13}+5\cdot 10^{13}=\)
- \((3\cdot 10^7)\cdot (2\cdot 10^{15})=\)
- \((5\cdot 10^{10})^3=\)
- \((6,5\cdot 10^{-4})\cdot (2\cdot 10^{-7})=\)
- \(\frac{4^7+4^7+4^7+4^7}{2^8}\cdot 4=\)
- \((4,8\cdot 10^{11}):(0,8\cdot 10^{-13})=\)
Zadanie 1. (1 pkt)
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Iloraz \(\frac{20^7}{4^7}\) jest równy A
B
. A.\( 5^7 \)
B.\( 16^7 \)
C
D
C.\( 24^{23} \)
D.\( 12^{14} \)
Zadanie 2. (1 pkt)
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
| Iloczyn \(8 \cdot 4^{3}\) jest równy wartości wyrażenia \(2^{9}\). | P | F |
| Wyrażenie \(\frac{3^{3} \cdot 3^{4}}{3^{5}}\) można zapisać w postaci \(3^{6}\). | P | F |
Zadanie 3. (1 pkt)
Liczba \((20\ 000)^3\) jest równa A.\( 2\cdot 10^{12} \)
B.\( 8\cdot 10^{12} \)
C.\( 20\cdot 10^{6} \)
D.\( 20\cdot 10^{12} \)
Zadanie 4. (2 pkt)
Ziemia ma masę \(5,97\cdot 10^{24}\) kg, a Księżyc ma masę \(7\cdot 10^{22}\) kg.- Jaka jest łączna masa Ziemi i Księżyca?
- Ile razy Ziemia jest cięższa od Księżyca?
Na filmie pokazuję jak analiza wykresu funkcji pomaga przy rozwiązywaniu nierówności.
- \(\sqrt{3}-(x-\sqrt{2})^2 \lt \frac{x}{\sqrt{5}}+\pi\)
- \(\sin x-1\ge 2^x\)
- \(|x^2-4|\ge|x|-2\)
Rozwiąż nierówności:
- \(\frac{3}{x} \geqslant 6\)
- \(\frac{x-3}{x+5}\gt 0\)
- \(\frac{8x}{x-3}\leqslant -1\)
W filmie pokazuję co to są asymptoty funkcji oraz jak je wyznaczać.
Czas nagrania: 34 min.
W trapezie narysowano przekątne. Które pole jest większe: \(P_1\) czy \(P_2\)? 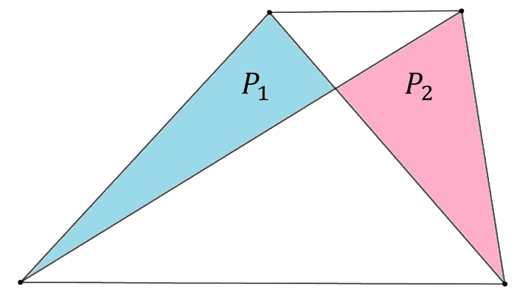

Wykaż, że \(\sqrt{23-8\sqrt{7}}=4-\sqrt{7}\).
W tym nagraniu opowiadam jak skutecznie zamieniać liczby rzymskie na arabskie i arabskie na rzymskie.
Wyznacz dziedzinę i rozwiąż równania:
- \(\frac{x+1}{x+2}=\frac{x+2}{x-3}\)
- \(\frac{x^2+2x}{x^2-1}=\frac{3}{(x-1)(x+1)}\)
- \(\frac{2}{x-3}+\frac{11x-2}{3x+6}=0\)
- \(\frac{1}{x}-\frac{5}{x^2}-\frac{6}{x^3}=0\)
- \(\frac{x+1}{4x-4}+\frac{1}{x}=-1\)
W nagraniu pokazuję jak można bez delty rozwiązać dowolne równanie kwadratowe.
Metodę pokazuję na kilku przykładach, gdzie najtrudniejszy to: \[2x^2-11x-15=0\] którego rozwiązaniami są liczby: \[x=\frac{11+\sqrt{241}}{4}\ \ \lor \ \ x=\frac{11-\sqrt{241}}{4}\]
Metodę pokazuję na kilku przykładach, gdzie najtrudniejszy to: \[2x^2-11x-15=0\] którego rozwiązaniami są liczby: \[x=\frac{11+\sqrt{241}}{4}\ \ \lor \ \ x=\frac{11-\sqrt{241}}{4}\]
Wykaż, że \(\sqrt{3\sqrt{3\sqrt{3\sqrt{3...}}}}=3\).
Która liczba jest większa: \(2024^{2025}\) czy \(\ 2025^{2024}\ \)?
Wykaż, że liczba \(2045^{2046}-1\) jest podzielna przez \(2047\).
zagadka - drogi
Udowodnij, że liczba \(\frac{15^{51}+13}{14}\) jest naturalna.
Wykaż, że liczba \(87^{99}+13^{99}\) jest podzielna przez \(25\).
Wykaż, że prawdziwa jest równość: \(\sqrt[3]{9+\sqrt{80}}+\sqrt[3]{9-\sqrt{80}}=3\)
Do szkolnego koła czytelniczego należy \(50\) uczniów. Opiekun koła zebrał dane dotyczące liczby książek przeczytanych przez tych uczniów w listopadzie 2024 roku. W poniższej tabeli przedstawiono wyniki zebrane przez opiekuna. 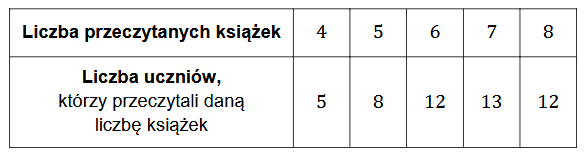
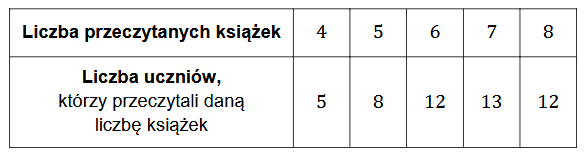
Uzupełnij zdania. Wpisz odpowiednie liczby w wykropkowanych miejscach, aby zdania były prawdziwe.
- Średnia arytmetyczna liczby przeczytanych książek w tej grupie uczniów jest równa ............ .
- Mediana liczby przeczytanych książek w tej grupie uczniów jest równa ............ .
Rozważamy wszystkie prostopadłościany \(ABCDEFGH\), w których krawędź \(AE\) jest \(3\) razy dłuższa od krawędzi \(A B\), a suma długości wszystkich dwunastu krawędzi prostopadłościanu jest równa \(48\) (zobacz rysunek). Niech \(P(x)\) oznacza funkcję pola powierzchni całkowitej takiego prostopadłościanu w zależności od długości \(x\) krawędzi \(AB\). 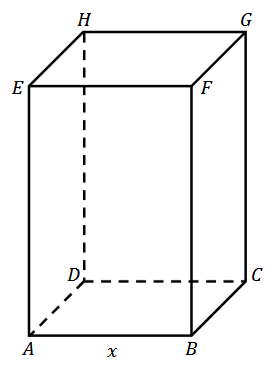

Wyznacz wzór i dziedzinę funkcji \(P\). Oblicz długość \(x\) krawędzi \(AB\) tego z rozważanych prostopadłościanów, którego pole powierzchni całkowitej jest największe. Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych pięciocyfrowych nieparzystych, w których zapisie dziesiętnym występują wyłącznie cyfry \(0,1,2,3\) (np. \(12303\), \(11111\)), jest A.\( 32 \)
B.\( 384 \)
C.\( 512 \)
D.\( 576 \)
Dane są dwa zbiory: \(C=\{1,2,3,4,5,6\}\) oraz \(D=\{7,8,9,10\}\). Losujemy jedną liczbę ze zbioru \(C\), a następnie losujemy jedną liczbę ze zbioru \(D\).
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że wylosujemy liczby, których iloczyn będzie podzielny przez \(4\). Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) dane są cztery okręgi: \(o_{1}, o_{2}, o_{3}, o_{4}\), o równaniach: \[ \begin{aligned} & o_{1}:(x-1)^{2}+(y-2)^{2}=1 \\[6pt] & o_{2}:(x+1)^{2}+(y+2)^{2}=9 \\[6pt] & o_{3}:(x-3)^{2}+(y-4)^{2}=4 \\[6pt] & o_{4}:(x+3)^{2}+(y+4)^{2}=16 \end{aligned} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Okręgiem, który nie ma żadnego punktu wspólnego z osiami układu współrzędnych \((x, y)\), jest A.\(o_{1}\)
B.\(o_{2}\)
C.\(o_{3}\)
D.\(o_{4}\)
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat o boku długości \(4\). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod takim kątem \(\alpha\), że \(\operatorname{tg} \alpha=3\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wysokość tego ostrosłupa jest równa A.\(3\)
B.\(6\)
C.\(6 \sqrt{2}\)
D.\(12\)
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są trzema kolejnymi parzystymi liczbami naturalnymi. Najdłuższa krawędź tego prostopadłościanu ma długość \(p\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Objętość tego prostopadłościanu jest równa A.\(p^{3}-3 p^{2}+2 p\)
B.\(p^{3}+3 p^{2}+2 p\)
C.\(p^{3}-6 p^{2}-8 p\)
D.\(p^{3}-6 p^{2}+8 p\)
Objętość stożka o wysokości \(2\) jest równa \(8 \pi\).
Oblicz miarę kąta rozwarcia tego stożka. Zapisz obliczenia.
W kartezjańskim układzie współrzędnych \((x, y)\) punkty \(A=(-2,-1)\) oraz \(C=(3,4)\) są przeciwległymi wierzchołkami kwadratu \(ABCD\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość boku kwadratu \(ABCD\) jest równa A.\(5\)
B.10
C.\(5 \sqrt{2}\)
D.\(\sqrt{10}\)
W kartezjańskim układzie współrzędnych \((x, y)\) dana jest prosta \(k\) o równaniu \(y=-7 x+3\). Prosta \(l\) jest równoległa do prostej \(k\) i przecina oś \(O y\) w punkcie \((0,6)\). Punkt o współrzędnych \((1, p)\) należy do prostej \(l\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(p\) jest równa A.\((-4)\)
B.\((-1)\)
C.\(\frac{5}{7}\)
D.\(7\)
Kąt o mierze \(\alpha\) jest rozwarty oraz \(\sin \alpha=\frac{\sqrt{3}}{4}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Cosinus kąta o mierze \(\alpha\) jest równy A.\(\left(-\frac{\sqrt{13}}{4}\right)\)
B.\(\left(-\frac{1}{2}\right)\)
C.\(\frac{1}{2}\)
D.\(\frac{\sqrt{13}}{4}\)
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość \(7{,}5\). Krótsza przekątna \(AC\) ma długość równą \(6\) i dzieli trapez na dwa trójkąty prostokątne (zobacz rysunek). 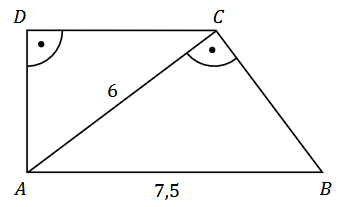

Oblicz pole trapezu \(ABCD\). Zapisz obliczenia.
Dany jest okrąg o środku w punkcie \(S\) i promieniu \(6\). Miara kąta wpisanego \(A C B\) jest równa \(60^{\circ}\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość łuku \(AB\), na którym oparty jest kąt wpisany \(ACB\), jest równa A.\(2 \pi\)
B.\(4 \pi\)
C.\(6 \pi\)
D.\(12 \pi\)
Funkcja logarytmiczna \(f\) jest określona wzorem \(f(x)=\log _{6} x\) dla każdej dodatniej liczby rzeczywistej \(x\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Wartość funkcji \(f\) dla argumentu \(36\) jest równa \(6\). | P | F |
| Funkcja \(f\) jest rosnąca. | P | F |
Ciąg \(\left(a_{n}\right)\) jest określony wzorem \(a_{n}=3 \cdot(-1)^{n}+10\) dla każdej liczby naturalnej \(n \geq 1\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Ciąg \(\left(a_{n}\right)\) jest geometryczny. | P | F |
| Suma ośmiu początkowych kolejnych wyrazów ciągu \(\left(a_{n}\right)\) jest równa \(80\). | P | F |
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Trzywyrazowy ciąg ( \(5 m, 4+2 m, m\) ) jest arytmetyczny, gdy liczba \(m\) jest równa A.\( (-4) \)
B.\( (-1) \)
C.\( 1 \)
D.\( 4 \)
Dany jest ciąg geometryczny \(\left(a_{n}\right)\) określony dla każdej liczby naturalnej \(n \geq 1\), w którym \(a_{2}=\frac{1}{6}\) oraz \(a_{3}=\frac{1}{9}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Piąty wyraz ciągu \(\left(a_{n}\right)\) jest równy A.\(\frac{1}{15}\)
B.\(\frac{2}{27}\)
C.\(\frac{4}{81}\)
D.\(\frac{8}{243}\)
Funkcja \(f\) jest określona następująco: \[ f(x)= \begin{cases}3 & \text { dla } x \in(-4,-2] \\ -x+1 & \text { dla } x \in(-2,2] \\ x-3 & \text { dla } x \in(2,4]\end{cases} \] Wykres funkcji \(y=f(x)\) przedstawiono w kartezjańskim układzie współrzędnych \((x, y)\) na rysunku poniżej. 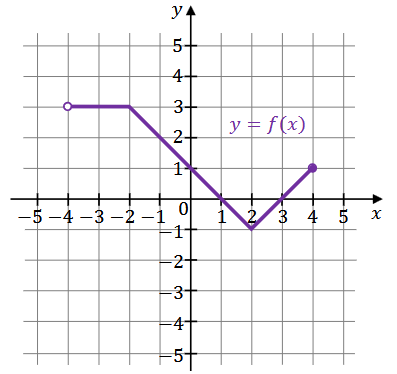
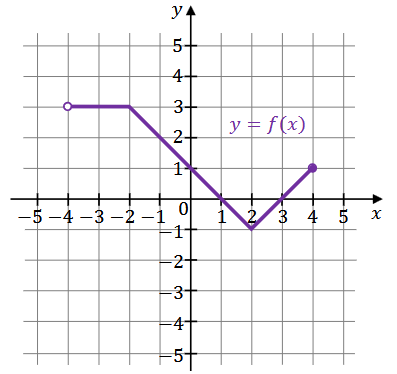
Uzupełnij zdania. Wpisz odpowiednie przedziały w wykropkowanych miejscach, aby zdania były prawdziwe.
- Dziedziną funkcji \(f\) jest przedział .............. .
- Zbiorem wartości funkcji \(f\) jest przedział .............. .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje wartości ujemne, jest przedział .............. .
- Zbiorem wszystkich argumentów, dla których funkcja \(f\) przyjmuje największą wartość, jest przedział .............. .
Miejscem zerowym funkcji liniowej \(f\) jest liczba 2, a punkt przecięcia wykresu funkcji \(f\) z osią \(O y\) kartezjańskiego układu współrzędnych \((x, y)\) ma współrzędne \((0,4)\) (zobacz rysunek). 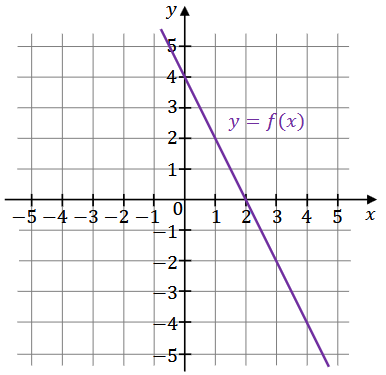
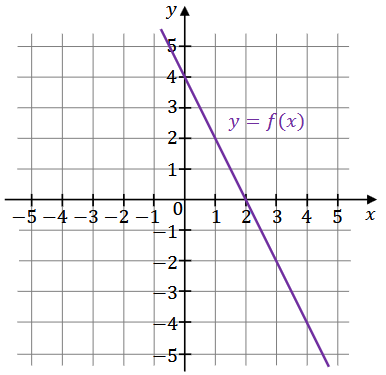
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Współczynnik kierunkowy prostej, która jest wykresem funkcji \(f\), jest równy \((-2)\). | P | F |
| Pole trójkąta ograniczonego osiami kartezjańskiego układu współrzędnych \((x, y)\) oraz wykresem funkcji \(f\) jest równe \(8\). | P | F |
Para liczb \(x=-1\) i \(y=6\) jest rozwiązaniem układu równań \[ \left\{\begin{array}{l} a x+3 y=20 \\ x+b y=5 \end{array}\right. \] gdzie \(a\) oraz \(b\) są liczbami rzeczywistymi.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia \(a \cdot b\) jest równa A.\((-2)\)
B.\((-0,5)\)
C.\(0,5\)
D.\(2\)
Rozwiąż równanie \[\frac{x+3}{x-1}=\frac{x}{2 x-2}\] Zapisz konieczne założenie i obliczenia.
Rozwiąż nierówność \[ x(x-6) \leq 7 \] Zapisz obliczenia.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(x\) różnej od \((-1)\), \(0\) oraz \(1\) wartość wyrażenia \(\frac{x}{x^{2}-1}: \frac{3 x^{2}}{x+1}\) jest równa wartości wyrażenia A.\(\frac{x}{x-1}\)
B.\(\frac{1}{3 x^{2}-3 x}\)
C.\(-3 x\)
D.\(-\frac{1}{3 x}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej dodatniej liczby rzeczywistej \(x\) i dla każdej dodatniej liczby rzeczywistej \(y\) wartość wyrażenia \(\log _{7} x+6 \log _{7} y\) jest równa wartości wyrażenia A.\(\log _{7}\left(\frac{x}{y^{6}}\right)\)
B.\(\log _{7}(x y)^{6}\)
C.\(\log _{7}(6 x y)\)
D.\(\log _{7}\left(x y^{6}\right)\)
Pani Aniela wpłaciła do banku kwotę \(60000\) zł na lokatę dwuletnią. Po każdym rocznym okresie oszczędzania bank doliczał odsetki w wysokości \(p \%\) w skali roku od kwoty bieżącego kapitału znajdującego się na lokacie - zgodnie z procentem składanym. Na koniec okresu oszczędzania kwota na tej lokacie była równa \(67925,76\) zł wraz z odsetkami (bez uwzględniania podatków).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Oprocentowanie lokaty w skali roku było równe A.\(6 \%\)
B.\(6,4 \%\)
C.\(6,5 \%\)
D.\(7 \%\)
Wykaż, że liczba \(2^{100}+4^{49}+16^{24}\) jest podzielna przez \(21\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\sqrt[5]{5} \cdot \frac{1}{5}\right)^{-5}\) jest równa A.\(5^{4}\)
B.\(5^{-4}\)
C.\(5^{0,25}\)
D.\(5^{-0,25}\)
Liczby \(x_{1}\) i \(x_{2}\) są różnymi rozwiązaniami równania \(|x+4|=7\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma \(x_{1}+x_{2}\) jest równa A.\((-14)\)
B.\((-8)\)
C.\(3\)
D.\(8\)
Tematy nadrzędne i sąsiednie