Ciekawe zadanka, zagadki i łamigłówki

Jak bez oderwania ołówka nakreślić figury zamieszczone na rysunkach?

Dwa kwadraty o boku długości \(1\) narysowano tak, że środek jednego pokrywa się z wierzchołkiem drugiego. Ile jest równe pole zamalowanej figury?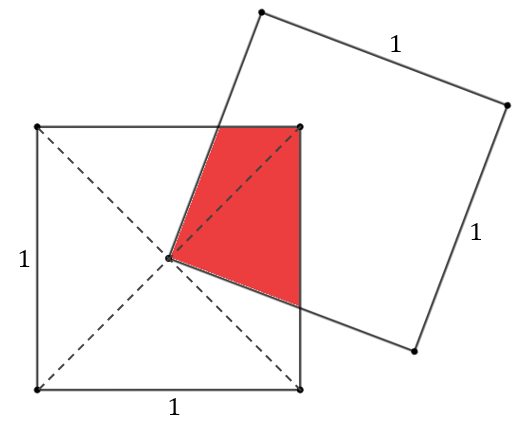

Przekątne czworokąta podzieliły go na \(4\) trójkąty. Znane są pola trzech trójkątów. Oblicz pole czwartego trójkąta.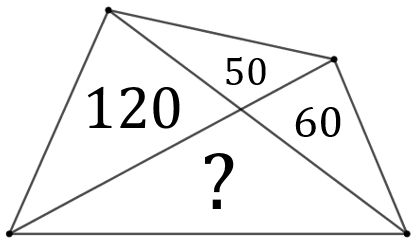

W kwadrat o boku długości \(1\) wpisano półokrąg i narysowano do niego odcinek styczny. Oblicz długość tego odcinka.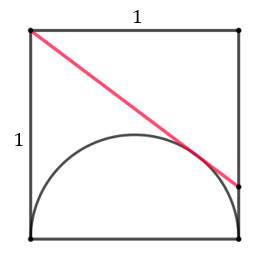

Nie odrywając długopisu od papieru narysuj \(4\) linie proste, tak aby połączyć wszystkie \(9\) punktów.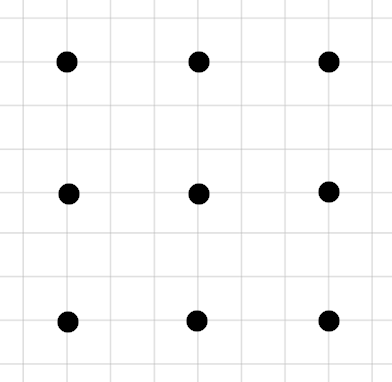

Ile kwadratów jest na rysunku?

W poniższym rozumowaniu jest błąd. Czy umiesz go wykryć? \[\begin{split} \text{Niech: }a=1,\ b=2:\\[6pt] a^2+b^2&=b^2+a^2\\[6pt] a^2-2ab+b^2&=b^2-2ab+a^2\\[6pt] (a-b)^2&=(b-a)^2\\[6pt] a-b&=b-a\\[6pt] 1-2&=2-1\\[6pt] -1&=1 \end{split}\] Oto kolejny przykład błędnego rozumowania: \[\begin{split} \text{Niech: }a=3,\ b=-3:\\[6pt] a+b&=0\\[6pt] a+b+(2a+2b)&=0+(2a+2b)\\[6pt] 3a+3b&=2a+2b\\[6pt] 3(a+b)&=2(a+b)\\[6pt] 3&=2 \end{split}\] Czy umiesz wskazać gdzie został popełniony błąd?

Na rysunku przedstawiono figurę wyznaczoną przez trzy półokręgi. Pola dwóch obszarów są znane. Ile wynosi pole trzeciego obszaru?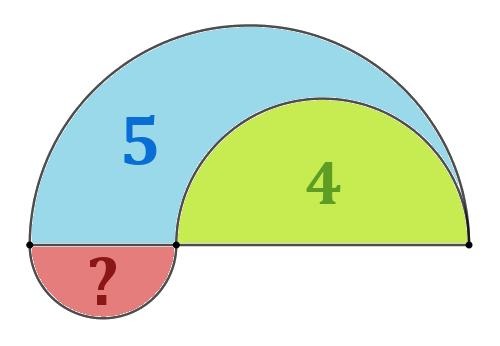

Ile trójkątów jest na każdym z rysunków?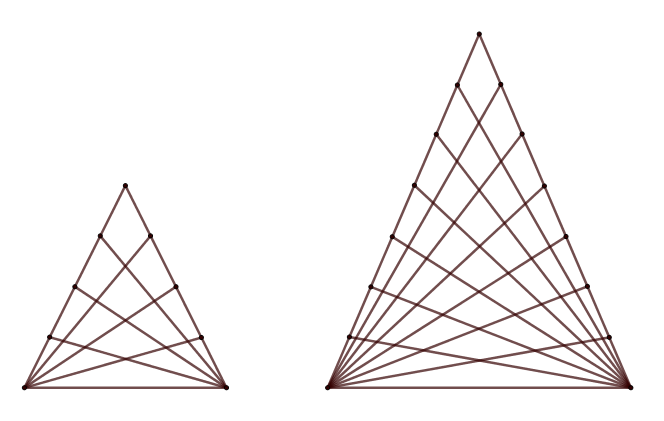

Poniższa figura została zbudowana z samych kwadratów. Ile kwadratów jest na rysunku?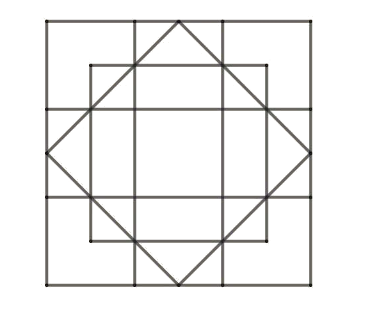

Ile trójkątów jest na rysunku?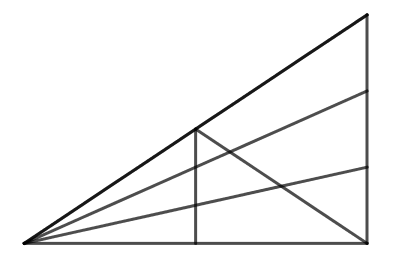

Filmik o bardzo dużych liczbach, postaci: \(9^{9^9}\).

Znajdź geometrycznie takie miejsce na autostradzie, aby suma długości dróg do miast \(A\) i \(B\) była jak najkrótsza.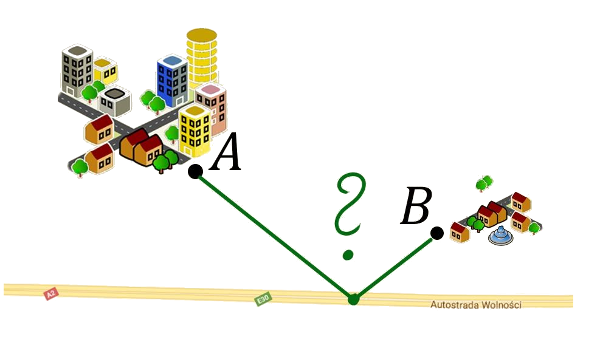

Pięć okręgów ma identyczne średnice. Wyznacz linię prostą przechodzącą przez punkt \(S\), która podzieli drut, z którego zrobiono okręgi, na pół.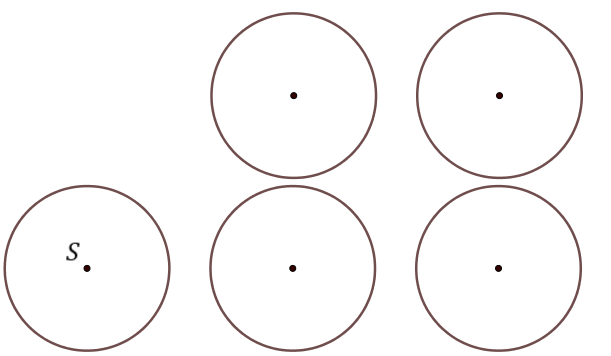

Witraż gotycki wyznaczają dwa okręgi przystające o środkach w punktach \(A\) i \(B\) i promieniu długości \(|AB|\) oraz odcinek \(AB\) (tak jak pokazano na rysunku). Oblicz pole części witraża zamalowanej na niebiesko, wiedząc, że \(|AB|=a\).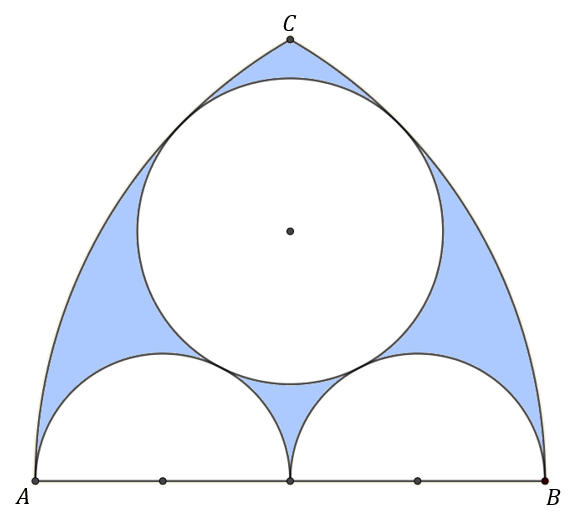

Ile jest najkrótszych dróg z punktu \(A\) do punktu \(B\)? Oddzielnie rozpatrz przypadek z rysunku pierwszego i drugiego.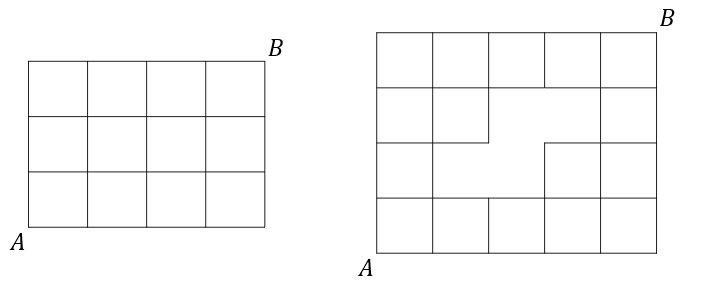

Dwa okręgi o promieniu \(2\) są styczne zewnętrznie. Ze środka jednego poprowadzone dwie styczne do drugiego okręgu. Oblicz zamalowane pole.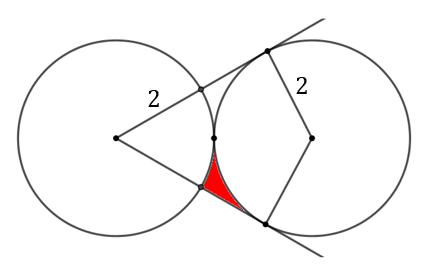

Jak dwiema liniami prostymi rozciąć krzyż na \(4\) identyczne części, aby można było z nich zbudować kwadrat?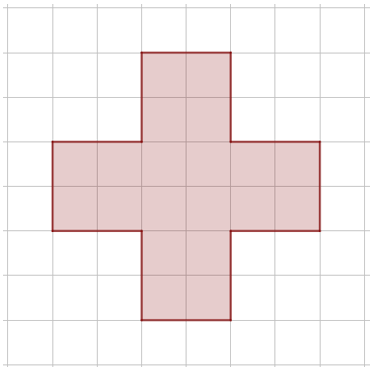

Narysuj \(3\) odcinki łączące boki prostokąta, aby oddzielić czerwone kółka od zielonych.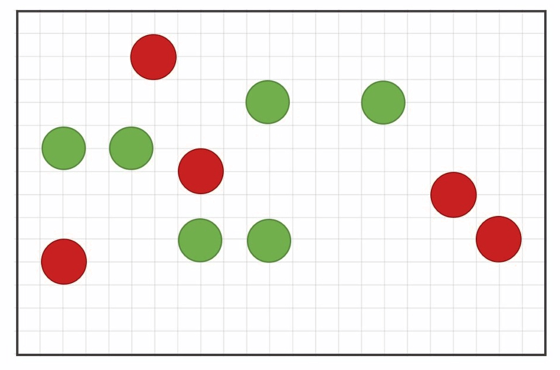

Na rysunku zaznaczono odcinki równej długości oraz trójkąt o polu \(10\). Ile wynosi pole trójkąta \(ABC\)?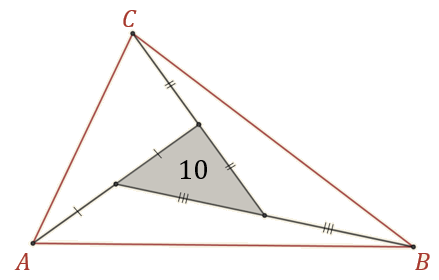

Fragment szarej figury wewnątrz okręgu obracamy o \(45^\circ \). W nowo otrzymanej figurze otrzymujemy o jeden czerwony odcinek mniej. Dlaczego?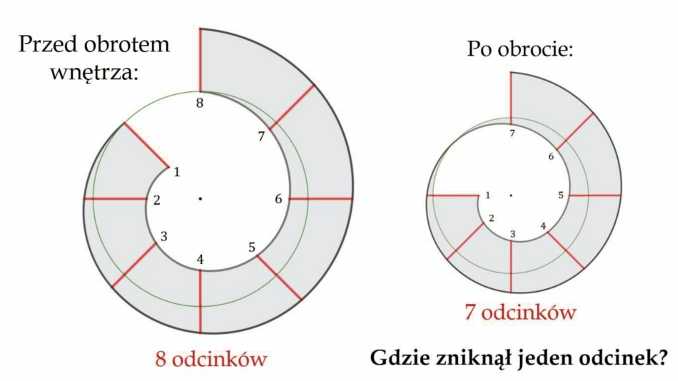

Na ile maksymalnie części można rozciąć podkowę dwiema liniami prostymi? 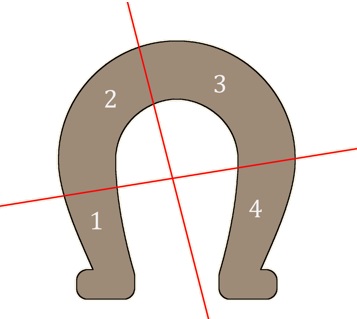Na powyższym rysunku jest przykładowe rozcięcie na 4 części.

Narysuj \(3\) linie proste, aby oddzielić wszystkie prezenty.

Jak za pomocą ekierki i ołówka wyznaczyć środek okręgu?

Ile trójkątów jest na rysunku?

Jak ustawić \(10\) taboretów pod ścianami w kwadratowym pokoju, aby pod każdą ścianą stało tyle samo taboretów?

Ile wynosi pole poniższej figury wyznaczonej za pomocą cyrkla o rozstawie 1?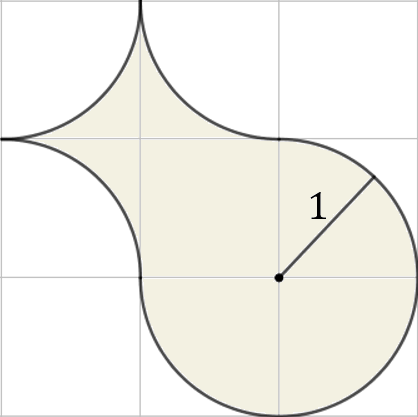

Zmień położenie 3 zapałek, aby otrzymać rybę skierowaną w odwrotnym kierunku.

Jaki jest poprawny kod?

Ile wynosi wynik ostatniego działania?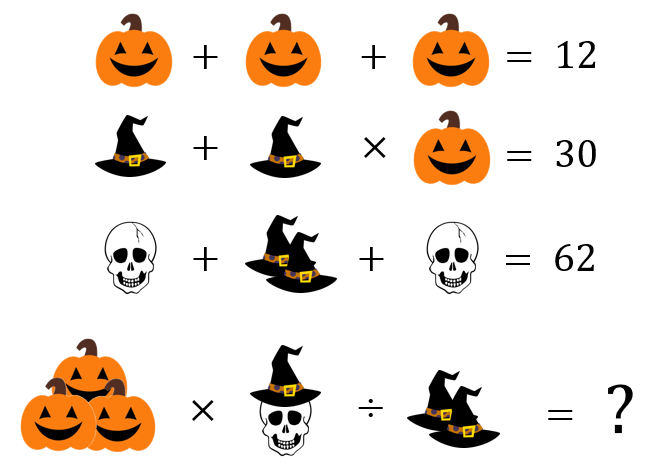

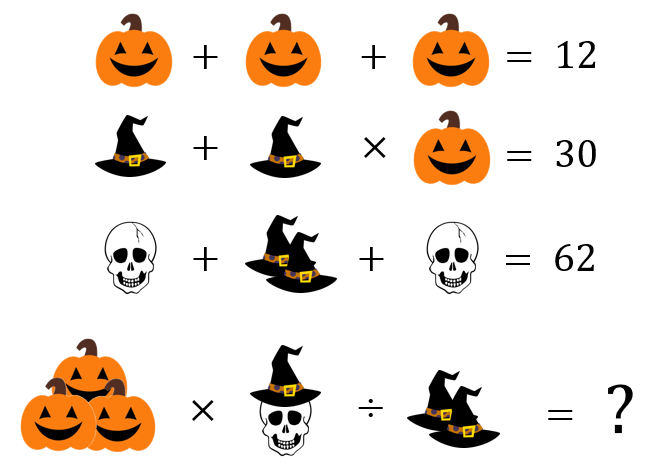
W obszarze ograniczonym jednym prostokątem jest \(4\) Mikołajów i \(4\) dzieci. Dorysuj 2 prostokąty w taki sposób, aby powstały cztery obszary, a w każdym z nich jeden Mikołaj i jedno dziecko.