Matura 2024 maj
Poziom podstawowy
Dana jest nierówność \[ |x-1| \geq 3 \] 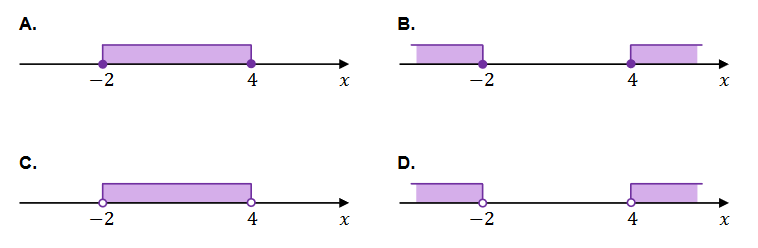
Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność? Wybierz właściwą odpowiedź spośród podanych.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\left(\frac{1}{16}\right)^8 \cdot 8^{16}\) jest równa A.\(2^{24}\)
B.\(2^{16}\)
C.\(2^{12}\)
D.\(2^8\)
Wykaż, że dla każdej liczby naturalnej \(n \geq 1\) liczba \(n^{2}+(n+1)^{2}+(n+2)^{2}\) przy dzieleniu przez \(3\) daje resztę \(2\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\log _{\sqrt{3}} 9\) jest równa A.\( 2 \)
B.\( 3 \)
C.\( 4 \)
D.\( 9 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej \(a\) i dla każdej liczby rzeczywistej \(b\) wartość wyrażenia \((2 a+b)^{2}-(2 a-b)^{2}\) jest równa wartości wyrażenia A.\(8 a^{2}\)
B.\(8 a b\)
C.\(-8 a b\)
D.\(2 b^{2}\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności \[ 1-\frac{3}{2} x<\frac{2}{3}-x \] jest przedział A.\(\left(-\infty,-\frac{2}{3}\right)\)
B.\(\left(-\infty, \frac{2}{3}\right)\)
C.\(\left(-\frac{2}{3},+\infty\right)\)
D.\(\left(\frac{2}{3},+\infty\right)\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie \(\frac{x+1}{(x+2)(x-3)}=0\) w zbiorze liczb rzeczywistych A.nie ma rozwiązania.
B.ma dokładnie jedno rozwiązanie: \((-1)\).
C.ma dokładnie dwa rozwiązania: \((-2)\) oraz 3.
D.ma dokładnie trzy rozwiązania: \((-1),(-2)\) oraz 3.
Dany jest wielomian \(W(x)=3 x^{3}+6 x^{2}+9 x\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Wielomian \(W\) jest iloczynem wielomianów \(F(x)=3 x\) i \(G(x)=x^{2}+2 x+3\). | P | F |
| Liczba \((-1)\) jest rozwiązaniem równania \(W(x)=0\). | P | F |
Rozwiąż równanie \[ x^{3}-2 x^{2}-3 x+6=0 \] Zapisz obliczenia.
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew.
Po roku stwierdzono, że uschło \(5 \%\) drzew w pierwszym sadzie i \(10 \%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(60 \%\) liczby drzew, które pozostały w pierwszym sadzie.
Niech \(x\) oraz \(y\) oznaczają liczby drzew posadzonych - odpowiednio - w pierwszym i drugim sadzie.
Po roku stwierdzono, że uschło \(5 \%\) drzew w pierwszym sadzie i \(10 \%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(60 \%\) liczby drzew, które pozostały w pierwszym sadzie.
Niech \(x\) oraz \(y\) oznaczają liczby drzew posadzonych - odpowiednio - w pierwszym i drugim sadzie.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby \(x\) drzew posadzonych w pierwszym sadzie oraz liczby \(y\) drzew posadzonych w drugim sadzie, jest A.\(\left\{\begin{array}{l}x+y=1960 \\ 0,6 \cdot 0,95 x=0,9 y\end{array}\right.\)
B.\(\left\{\begin{array}{l}x+y=1960 \\ 0,95 x=0,6 \cdot 0,9 y\end{array}\right.\)
C.\(\left\{\begin{array}{l}x+y=1960 \\ 0,05 x=0,6 \cdot 0,1 y\end{array}\right.\)
D.\(\left\{\begin{array}{l}x+y=1960 \\ 0,4 \cdot 0,95 x=0,9 y\end{array}\right.\)
Na rysunku, w kartezjańskim układzie współrzędnych \((x, y)\), przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego \(z\) poniższych układów równań A-D. 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest A.\(\left\{\begin{array}{l}y=-\frac{3}{2} x+3 \\ y=-\frac{3}{2} x-1\end{array}\right.\)
B.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=-\frac{2}{3} x-1\end{array}\right.\)
C.\(\left\{\begin{array}{l}y=\frac{3}{2} x+3 \\ y=\frac{3}{2} x-1\end{array}\right.\)
D.\(\left\{\begin{array}{l}y=-\frac{3}{2} x-3 \\ y=\frac{3}{2} x+1\end{array}\right.\)
Funkcja liniowa \(f\) jest określona wzorem \(f(x)=(-2 k+3) x+k-1\), gdzie \(k \in \mathbb{R}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja \(f\) jest malejąca dla każdej liczby \(k\) należącej do przedziału A.\((-\infty, 1)\)
B.\(\left(-\infty,-\frac{3}{2}\right)\)
C.\((1,+\infty)\)
D.\(\left(\frac{3}{2},+\infty\right)\)
Funkcje liniowe \(f\) oraz \(g\), określone wzorami \(f(x)=3 x+6\) oraz \(g(x)=a x+7\), mają to samo miejsce zerowe.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współczynnik \(a\) we wzorze funkcji \(g\) jest równy A.\(\left(-\frac{7}{2}\right)\)
B.\(\left(-\frac{2}{7}\right)\)
C.\(\frac{2}{7}\)
D.\(\frac{7}{2}\)
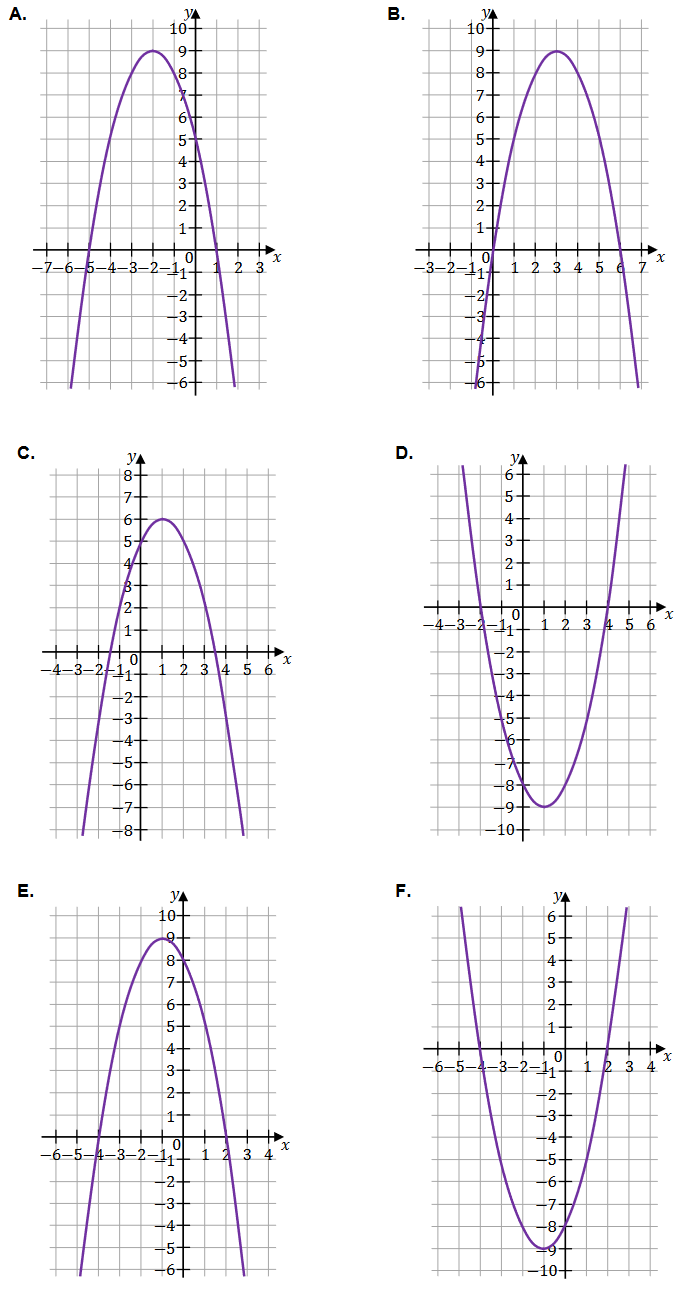
W kartezjańskim układzie współrzędnych \((x, y)\) przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej \(f\) (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite. 

Uzupełnij poniższe zdanie. Wpisz odpowiedni przedział w wykropkowanym miejscu tak, aby zdanie było prawdziwe.
Zbiorem wszystkich rozwiązań nierówności \(f(x) \geq 0\) jest przedział \(.......................\) .Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja kwadratowa \(f\) jest określona wzorem A.\(f(x)=-(x+1)^{2}-9\)
B.\(f(x)=-(x-1)^{2}+9\)
C.\(f(x)=-(x-1)^{2}-9\)
D.\(f(x)=-(x+1)^{2}+9\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla funkcji \(f\) prawdziwa jest równość A. \(f(-4)=f(6)\)
B.\(f(-4)=f(5)\)
C.\(f(-4)=f(4)\)
D.\(f(-4)=f(7)\)
Funkcje kwadratowe \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) (zobacz rysunek na stronie 13) następująco: \(g(x)=f(x+3)\), \(h(x)=f(-x)\).
Na rysunkach A-F przedstawiono, w kartezjańskim układzie współrzędnych \((x, y)\), fragmenty wykresów różnych funkcji - w tym fragment wykresu funkcji \(g\) oraz fragment wykresu funkcji \(h\).
Uzupełnij tabelę. Każdej \(z\) funkcji \(g\) oraz \(h\) przyporządkuj fragment jej wykresu. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A-F.
| Fragment wykresu funkcji \(y=g(x)\) przedstawiono na rysunku | |
| Fragment wykresu funkcji \(y=h(x)\) przedstawiono na rysunku |
Ciąg \(\left(a_{n}\right)\) jest określony wzorem \(a_{n}=(-1)^{n} \cdot(n-5)\) dla każdej liczby naturalnej \(n \geq 1\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
| Pierwszy wyraz ciągu \(\left(a_{n}\right)\) jest dwa razy większy od trzeciego wyrazu tego ciągu. | P | F |
| Wszystkie wyrazy ciągu \(\left(a_{n}\right)\) są dodatnie. | P | F |
Trzywyrazowy ciąg \((12,6,2 m-1)\) jest geometryczny. 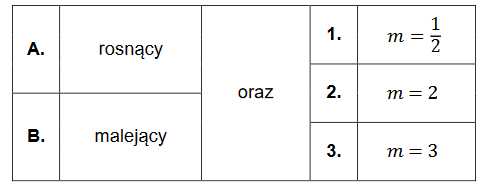
Dokończ zdanie. Wybierz odpowiedź A albo B oraz odpowiedź 1., 2. albo 3.
Ten ciąg jest 
Ciąg arytmetyczny \(\left(a_{n}\right)\) jest określony dla każdej liczby naturalnej \(n \geq 1\). Trzeci wyraz tego ciągu jest równy \((-1)\), a suma piętnastu początkowych kolejnych wyrazów tego ciągu jest równa \((-165)\).
Oblicz różnicę tego ciągu. Zapisz obliczenia.
W kartezjańskim układzie wspórzędnych \((x, y)\) zaznaczono kąt o mierze \(\alpha\) taki, że \(\operatorname{tg} \alpha=-3\) oraz \(90^{\circ}<\alpha<180^{\circ}\) (zobacz rysunek). 

Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Prawdziwe są zależności: ............. oraz .............. . A.\(\sin \alpha<0\)
B.\(\sin \alpha \cdot \cos \alpha<0\)
C.\(\sin \alpha \cdot \cos \alpha>0\)
D.\(\cos \alpha>0\)
E.\(\sin \alpha=-\frac{1}{3} \cos \alpha\)
F.\(\sin \alpha=-3 \cos \alpha\)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(\sin ^{3} 20^{\circ}+\cos ^{2} 20^{\circ} \cdot \sin 20^{\circ}\) jest równa A.\(\cos 20^{\circ}\)
B.\(\sin 20^{\circ}\)
C.\(\operatorname{tg} 20^{\circ}\)
D.\(\sin 20^{\circ} \cdot \cos 20^{\circ}\)
Dany jest trójkąt \(K L M\), w którym \(|K M|=a,|L M|=b\) oraz \(a \neq b\). Dwusieczna kąta \(K M L\) przecina bok \(K L\) w punkcie \(N\) takim, że \(|K N|=c\), \(|N L|=d\) oraz \(|M N|=e\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
W trójkącie \(K L M\) prawdziwa jest równość A.\( a \cdot b=c \cdot d \)
B.\( a \cdot d=b \cdot c \)
C.\( a \cdot c=b \cdot d \)
D.\( a \cdot b=e \cdot e \)
Dany jest równoległobok o bokach długości \(3\) i \(4\) oraz o kącie między nimi o mierze \(120^{\circ}\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego równoległoboku jest równe A.\( 12 \)
B.\( 12 \sqrt{3} \)
C.\( 6 \)
D.\( 6 \sqrt{3} \)
W trójkącie \(A B C\), wpisanym w okrąg o środku w punkcie \(S\), kąt \(A C B\) ma miarę \(42^{\circ}\) (zobacz rysunek). 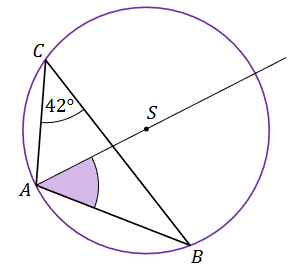

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta ostrego \(B A S\) jest równa A.\( 42^{\circ} \)
B.\( 45^{\circ} \)
C.\( 48^{\circ} \)
D.\( 69^{\circ} \)
W kartezjańskim układzie współrzędnych \((x, y)\) proste \(k\) oraz \(l\) są określone równaniami \[ \begin{aligned} & k: y=(m+1) x+7 \\ & l: y=-2 x+7 \end{aligned} \]
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Proste \(k\) oraz \(l\) są prostopadłe, gdy liczba \(m\) jest równa A.\( \left(-\frac{1}{2}\right) \)
B.\( \frac{1}{2} \)
C.\( (-3) \)
D.\( 1 \)
W kartezjańskim układzie współrzędnych \((x, y)\) dany jest równoległobok \(A B C D\), w którym \(A=(-2,6)\) oraz \(B=(10,2)\). Przekątne \(A C\) oraz \(B D\) tego równoległoboku przecinają się w punkcie \(P=(6,7)\).
Oblicz długość boku \(B C\) tego równoległoboku. Zapisz obliczenia.
Wysokość graniastosłupa prawidłowego sześciokątnego jest równa \(6\) (zobacz rysunek). Pole podstawy tego graniastosłupa jest równe \(15 \sqrt{3}\). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole jednej ściany bocznej tego graniastosłupa jest równe A.\(36 \sqrt{10}\)
B.\( 60 \)
C.\( 6 \sqrt{10} \)
D.\( 360 \)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku 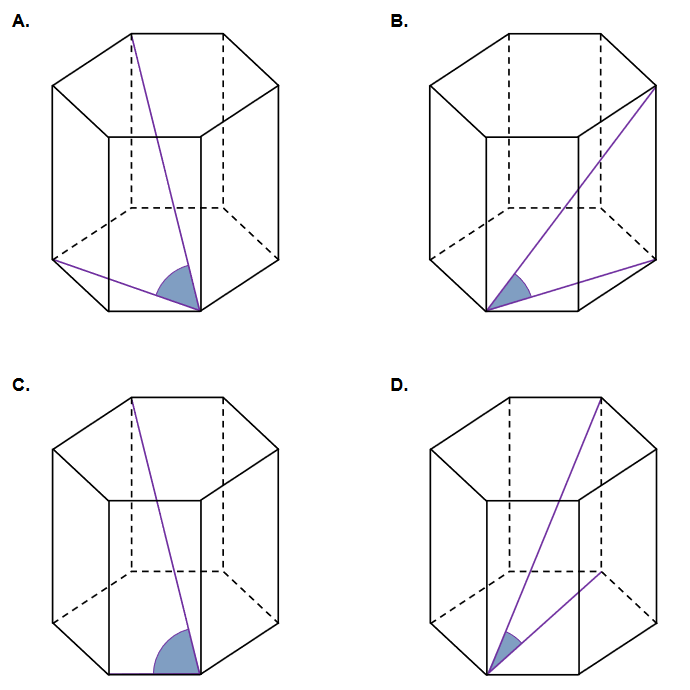
Ostrosłup \(F_{1}\) jest podobny do ostrosłupa \(F_{2}\).
Objętość ostrosłupa \(F_{1}\) jest równa \(64\).
Objętość ostrosłupa \(F_{2}\) jest równa \(512\).
Objętość ostrosłupa \(F_{1}\) jest równa \(64\).
Objętość ostrosłupa \(F_{2}\) jest równa \(512\).
Uzupełnij poniższe zdanie. Wpisz odpowiednią liczbę w wykropkowanym miejscu tak, aby zdanie było prawdziwe.
Stosunek pola powierzchni całkowitej ostrosłupa \(F_{2}\) do pola powierzchni całkowitej ostrosłupa \(F_{1}\) jest równy ...........Rozważamy wszystkie kody czterocyfrowe utworzone tylko z cyfr \(1,\ 3,\ 6,\ 8\), przy czym w każdym kodzie każda z tych cyfr występuje dokładnie jeden raz.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba wszystkich takich kodów jest równa A.\( 4 \)
B.\( 10 \)
C.\( 24 \)
D.\( 16 \)
Średnia arytmetyczna trzech liczb: \(a,\ b,\ c\), jest równa \(9\).
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnia arytmetyczna sześciu liczb: \(a,\ a,\ b,\ b,\ c,\ c\), jest równa A.\( 9 \)
B.\( 6 \)
C.\( 4{,}5 \)
D.\( 18 \)
\(\mathrm{Na}\) diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę. 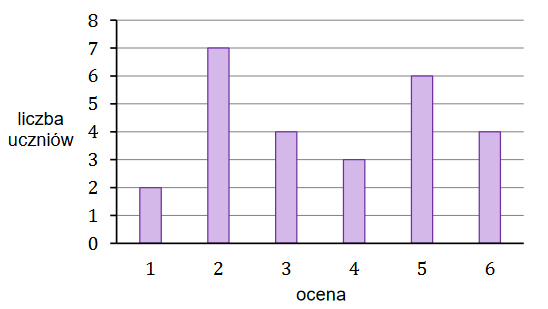

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Mediana ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa A.\( 4{,}5 \)
B.\( 4 \)
C.\( 3{,}5 \)
D.\( 3 \)
Dany jest pięcioelementowy zbiór \(K=\{5,6,7,8,9\}\). Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru \(K\) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą. Zapisz obliczenia.
W schronisku dla zwierząt, na płaskiej powierzchni, należy zbudować ogrodzenie z siatki wydzielające trzy identyczne wybiegi o wspólnych ścianach wewnętrznych.
Podstawą każdego z tych trzech wybiegów jest prostokąt (jak pokazano na rysunku).
Do wykonania tego ogrodzenia należy zużyć \(36\) metrów bieżących siatki.
Schematyczny rysunek trzech wybiegów (widok z góry). Linią przerywaną zaznaczono siatkę.
Podstawą każdego z tych trzech wybiegów jest prostokąt (jak pokazano na rysunku).
Do wykonania tego ogrodzenia należy zużyć \(36\) metrów bieżących siatki.
Schematyczny rysunek trzech wybiegów (widok z góry). Linią przerywaną zaznaczono siatkę.

Oblicz wymiary \(x\) oraz \(y\) jednego wybiegu, przy których suma pól podstaw tych trzech wybiegów będzie największa. W obliczeniach pomiń szerokość wejścia na każdy z wybiegów. Zapisz obliczenia.
Tematy nadrzędne i sąsiednie