Dzielenie ułamków dziesiętnych

Drukuj

Szkoła podstawowa

Ułamki dziesiętne dzielimy tak:

Przesuwamy przecinek w prawo w obu liczbach w taki sposób, aby dzielna stała się liczbą całkowitą, np.: \[0{,}35 : 0{,}5 =3{,}5:5\] Taka operacja nie zmienia wyniku dzielenia, ponieważ jest to pomnożenie dzielnej i dzielnika przez taką samą liczbę: \(10\), \(100\), lub \(1000\).
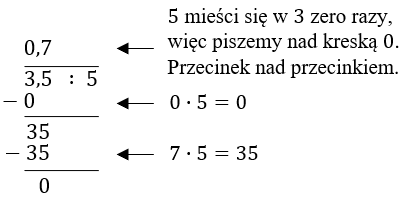
Czyli wykonujemy rozszerzenie ułamka: \[0{,}35 : 0{,}5 =\frac{0{,}35}{0{,}5}=\frac{0{,}35\cdot 10}{0{,}5\cdot 10}=\frac{3,5}{5}=3{,}5:5\]
Następnie wykonujemy dzielenie w głowie \(3{,}5:5= 0{,}7\) lub pisemnie. Dzielenie pisemne wykonujemy tak jak dzielenie pisemnie liczb całkowitych, a przecinek przepisujemy nad przecinkiem:

Dobrym sposobem na wykonanie dzielenie ułamków dziesiętnych jest wcześniejsza ich zamiana na ułamki zwykłe (o ile nauczyciel na to pozwala).

Wykonaj dzielenie \(6{,}24 : 4\).

Dzielnik jest już liczbą całkowitą, więc od razu wykonujemy dzielenie pisemne: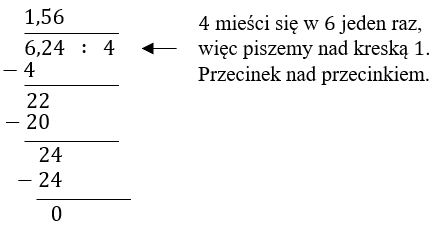

Rachunek na ułamkach zwykłych: \[6{,}24 : 4 = \frac{624}{100}\cdot \frac{1}{4}=\frac{156}{100}=1{,}56\]

Podziel pisemnie ułamki \(124{,}28 : 5{,}2\).

Na początku w obu ułamkach przesuwamy przecinek o jeden prawo, aby z dzielnika zrobiła się liczba całkowita: \[124{,}28 : 5{,}2=1242{,}8 : 52\] Wykonujemy dzielenie pisemne liczb:

Zatem: \[124{,}28 : 5{,}2=23{,}9\]