Dodawanie i odejmowanie ułamków dziesiętnych
Szkoła podstawowa
Proste działania na ułamkach dziesiętnych można wykonywać w głowie. Wystarczy dodać oddzielnie części całkowite i oddzielnie części ułamkowe.
\(0{,}1 + 0{,}3 = 0{,}4\)
\(1{,}4 + 2{,}5 = 3{,}9\)
\(11{,}7 - 0{,}3 = 11{,}4\)
\(6{,}9 - 3{,}5 = 3{,}4\)
Bardziej skomplikowane działania można wykonać pisemnie.
W tym celu zapisujemy dwa ułamki w słupku w taki sposób, aby przecinek jednego ułamka znalazł się pod przecinkiem drugiego ułamka. Jeżeli ułamki mają różną liczbę cyfr po przecinku, to do "krótszego" ułamka dopisujemy tyle zer, żeby części ułamkowe były równej długości.
W wyniku końcowym przecinek przepisujemy w tym samym miejscu, w którym występował w liczbach dodawanych.
W tym celu zapisujemy dwa ułamki w słupku w taki sposób, aby przecinek jednego ułamka znalazł się pod przecinkiem drugiego ułamka. Jeżeli ułamki mają różną liczbę cyfr po przecinku, to do "krótszego" ułamka dopisujemy tyle zer, żeby części ułamkowe były równej długości.
W wyniku końcowym przecinek przepisujemy w tym samym miejscu, w którym występował w liczbach dodawanych.
\(1{,}8 + 3{,}9 = 5{,}7\)
Teraz to samo działanie wykonamy w sposób pisemny: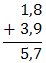
Teraz to samo działanie wykonamy w sposób pisemny:
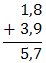
\(5{,}317 + 2{,}42 = 7{,}737\)
Teraz dodamy te dwa ułamki w sposób pisemny: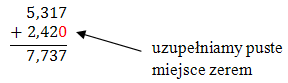
Teraz dodamy te dwa ułamki w sposób pisemny:
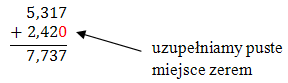
\(3{,}1 + 9{,}523 = 12{,}623\)
Teraz dodamy te dwa ułamki w sposób pisemny: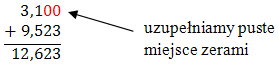
Teraz dodamy te dwa ułamki w sposób pisemny:
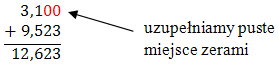
\(0{,}2 + 12{,}998 = 13{,}198\)
Teraz dodamy te dwa ułamki w sposób pisemny: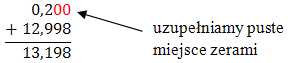
Teraz dodamy te dwa ułamki w sposób pisemny:
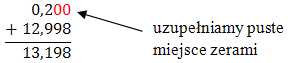
\(15{,}3 - 7{,}211 = 8{,}089\)
Teraz odejmiemy te dwa ułamki w sposób pisemny: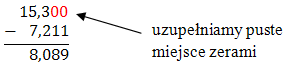
Teraz odejmiemy te dwa ułamki w sposób pisemny:
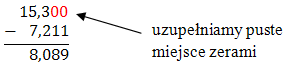
Tematy nadrzędne i sąsiednie