Zbiory

Poziom podstawowy

Zbiory oznaczamy wielkimi literami.
Elementy zbioru zapisujemy w nawiasach klamrowych i oddzielamy przecinkami.

Najczęściej spotykamy zbiory liczbowe, którego elementami są liczby.

\(\mathbb{N} = \{0,1,2,3,4,5,...\}\) - zbiór liczb naturalnych
\(A = \{2, 4, 6, 8,...\}\) - zbiór liczb parzystych dodatnich
\(B = \{0,1,2,3,4,5,6,7,8,9\}\) - zbiór cyfr

Definicja

Zbiór skończony - to zbiór, który ma skończoną liczbę elementów.
Zbiór nieskończony - to zbiór który ma nieskończenie wiele elementów.
Zbiór pusty - to zbiór do którego nie należy żaden element. Zbiór pusty oznaczamy symbolem \(\emptyset \).

Jeżeli chcemy zapisać, że element należy do zbioru, to używamy symbolu \(\in \), np. \(5\in \mathbb{N} \) lub \(\frac{3}{4}\in \mathbb{Q} \).
Aby zapisać, że element nie należy do zbioru, to używamy symbolu \(\notin \), np. \(\frac{1}{2}\notin \mathbb{N} \) lub \(\sqrt{2}\notin \mathbb{Q} \).

Zbiory można zapisywać podając warunek, który mają spełniać jego elementy.

\(A=\{x\in \mathbb{N}: x^2\leqslant 9\}\), to zbiór \(A=\{0,1,2,3\}\).
\(\mathbb{Q} =\{x: x=\frac{p}{q}\ \text{ i }\ p,q\in \mathbb{Z}\ \text{ i }\ q\ne 0\}\) - zbiór liczb wymiernych

Definicja

Zbiory \(A\) i \(B\) są równe wtedy i tylko wtedy, gdy maję te same elementy. Zapisujemy to: \[A=B\]

Zapis \(A\ne B\) oznacza, że zbiory nie są równe.

Sprawdź które spośród zbiorów \(A\), \(B\) i \(C\) są równe?
\(A=\{x\in \mathbb{N}: x^2\lt 9\}\)
\(B=\{0,1,2,3\}\)
\(C\) - zbiór cyfr potrzebnych do zapisania liczby \(12001\)

Określamy dokładnie zbiory:
\(A=\{0, 1, 2\}\) (liczba \(3\notin A\), ponieważ nierówność jest ostra),
\(B=\{0,1,2,3\}\)
\(C=\{1,2,0\}\).
Zatem mamy \(A = C\), \(A \ne B\) i \(B \ne C\).

Definicja

Zbiór \(A\) jest podzbiorem zbioru \(B\) wtedy i tylko wtedy, gdy każdy element zbioru \(A\) jest elementem zbioru \(B\). Zapisujemy to: \[A\subset B\] Mówimy też, że zbiór \(A\) zawiera się w zbiorze \(B\).

Zapis \(A\not\subset B\) oznacza, że \(A\) nie jest zawarty w \(B\).
Podzbiorem każdego zbioru \(A\) jest ten sam zbiór \(A\) oraz zbiór pusty, czyli: \(A\subset A\) oraz \(\emptyset \subset A\).

Dla poznanych zbiorów liczbowych zachodzą następujące zawierania: \[\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \]

Niech \(A=\{1,2,3\}\), \(B=\{3,4,5\}\) oraz \(C=\{1,2,3,4,5,6,7\}\). Wówczas mamy: \[A\subset C\ \ \text{i}\ \ B\subset C\]

Niech \(A=\{-5,5\}\) oraz \(B=\{x\in \mathbb{R}: x^2=25\}\). Wówczas mamy równość zbirów: \(A=B\), czyli: \[A\subset B\ \ \text{i}\ \ B\subset A\]

Definicja

Zbiory które rozpatrujemy są często podzbiorami pewnego większego zbioru. Taki nadrzędny zbiór nazywamy przestrzenią.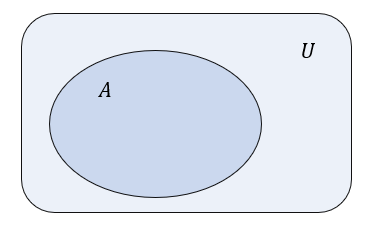

Przestrzeń oznaczamy często literą \(U\).

Przestrzenią dla zbiorów liczbowych jest często zbiór liczb rzeczywistych.