Działania na zbiorach

Drukuj

Poziom podstawowy

Definicja

Iloczynem zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą jednocześnie do zbioru \(A\) i do zbioru \(B\).
Iloczyn zbiorów \(A\) i \(B\) oznaczamy \(A\cap B\). \[A\cap B=\{x: x\in A\ \ \text{i}\ \ x\in B\}\]

Ilustracja na diagramie:

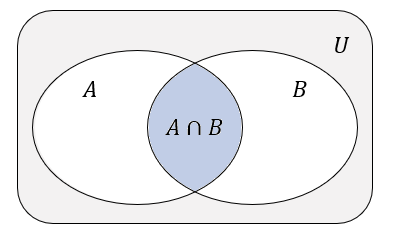
Iloczyn zbiorów \(A\cap B\)

\(A = \{1, 2, 3, 4, 5\}\), \(B = \{4, 5, 6, 7, 8\}\), to: \(A\cap B=\{4, 5\}\).

\(A = \left\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}\right\}\), \(B = \left\{\frac{2}{4}, \frac{2}{5}, \frac{2}{6}, \frac{2}{7}, \frac{2}{8}\right\}\), to: \(A\cap B=\left\{\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\right\}\).

\(A = \{a,\ b,\ c,\ d,\ e,\ f\}\), \(B = \{c,\ f,\ g,\ j\}\), to: \(A\cap B=\{c, f\}\).

\(A = \{a,\ b,\ c,\ d\}\), \(B = \{e,\ f,\ g,\ h\}\), to: \(A\cap B=\emptyset \).

W podpunkcie d) zbiory \(A\) i \(B\) nie mają wspólnych elementów. Takie zbiory nazywamy rozłącznymi. Iloczyn zbiorów rozłącznych jest zbiorem pustym.

Określ czy podane zbiory są rozłączne.

\(A\) - zbiór liczb parzystych, \(B\) - zbiór liczb nieparzystych.

\(C\) - zbiór liczb nieujemnych, \(D\) - zbiór liczb niedodatnich.

\(E\) - zbiór liter tworzących słowo "długopis", \(F\) - zbiór liter tworzących słowo "ołówek".

Liczba nie może być jednocześnie parzysta i nieparzysta, czyli zbiory \(A\) i \(B\) są rozłączne.

Do obu zbiorów należy liczba \(0\), zatem zbiory nie są rozłączne: \(C\cap D=\{0\} \).

Do obu zbiorów należą litery \(ł\) i \(o\), zatem zbiory nie są rozłączne: \(E\cap F=\{ł, o\} \).

Definicja

Sumą zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą do co najmniej jednego ze zbiorów \(A\) lub \(B\).
Sumę zbiorów \(A\) i \(B\) oznaczamy \(A\cup B\). \[A\cup B=\{x: x\in A\ \ \text{lub}\ \ x\in B\}\]

Ilustracja na diagramie:

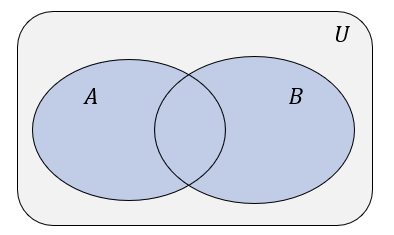
Suma zbiorów \(A\cup B\)

\(A = \{1, 2, 3\}\), \(B = \{5, 6, 7, 8\}\), to: \(A \cup B = \{1, 2, 3, 5, 6, 7, 8\}\).

\(A = \{-2,1,5\}\), \(B = \{1,5,7,12\}\), to: \(A \cup B = \{-2,1,5,7,12\}\).

\(A = \{a,\ b,\ c\}\), \(B = \{x\}\), to: \(A \cup B = \{a,\ b,\ c,\ x\}\).

\(A\) - zbiór dzielników liczby \(5\), \(B\) - zbiór dzielników liczby \(6\), to: \(A \cup B = \{1, 2, 3, 5, 6\}\).

Na diagramie przedstawiono zbiory \(A\), \(B\) i \(C\),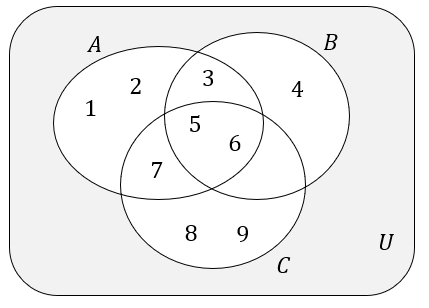

Dla tego przykładu mamy:
\(A=\{1,2,3,5,6,7\}\)
\(B=\{3,4,5,6\}\)
\(C=\{5,6,7,8,9\}\)
\(A\cap B=\{3,5,6\}\)
\(A\cap C=\{5,6,7\}\)
\(B\cap C=\{5,6\}\)
\(A\cap B\cap C=\{5,6\}\)
\(A\cup B=\{1,2,3,4,5,6,7\}\)
\(A\cup C=\{1,2,3,5,6,7,8,9\}\)
\(B\cup C=\{3,4,5,6,7,8,9\}\)
\(A\cup B\cup C=\{1,2,3,4,5,6,7,8,9\}\)

Definicja

Różnicą zbiorów \(A\) i \(B\) nazywamy zbiór elementów, które należą do zbioru \(A\) i nie należą do zbioru \(B\).
Różnicę zbiorów \(A\) i \(B\) oznaczamy \(A \backslash B\). \[A\backslash B=\{x: x\in A\ \ \text{i}\ \ x\notin B\}\]

Ilustracja na diagramie:

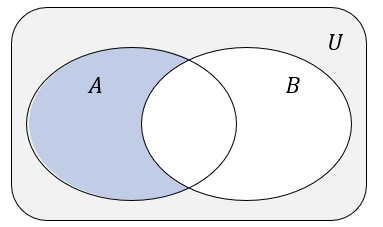
Różnica zbiorów \(A\backslash B\)

I analogicznie w drugą stronę: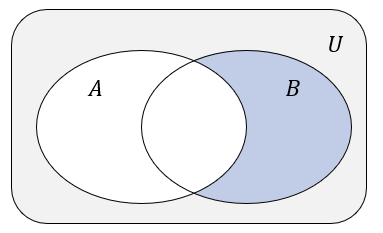

Różnica zbiorów \(B\backslash A\)

\(A = \{1, 2, 3, 4, 5\}\), \(B = \{4, 5, 6, 7, 8\}\), to: \(A \backslash B = \{1, 2, 3\}\) oraz \(B \backslash A = \{6, 7, 8\}\).

\(A = \{1, 2, 3\}\), \(B = \{4, 5, 6\}\), to: \(A \backslash B = A\) oraz \(B \backslash A = B\).

\(A = \{a,\ b,\ c\}\), \(B = \{a,\ b,\ c,\ d\}\), to: \(A \backslash B = \emptyset \) oraz \(B \backslash A = \{d\} \).

Dla zbiorów \(A\), \(B\) i \(C\) przedstawionych na diagramie określimy wybrane różnice

\[A \backslash B = \{1,2,7\}\] \[B \backslash C = \{4,3\}\] \[C \backslash A = \{8,9\}\] Ponadto: \[A \backslash (B\cup C) = \{1,2\}\] \[A \backslash (B\cap C) = \{1,2,3,7\}\] \[B \backslash (C\cap A) = \{3,4\}\]

Definicja

Dopełnieniem zbioru \(A\) nazywamy różnicę całej przestrzeni i zbioru \(A\) i oznaczamy: \(A'\). \[A'=U\backslash A=\{x: x\in U\ \ \text{i}\ \ x\notin A\}\]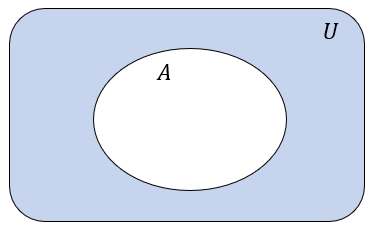

Ilustracja na diagramie:

Dopełnienie zbioru \(A\)

Rozpatrzmy przestrzeń liczb całkowitych \(\mathbb{Z} \).
Niech \(A\) - to podzbiór liczb parzystych bez liczby \(6\) w przestrzeni \(\mathbb{Z} \).
Wówczas \(A' = \mathbb{Z} \backslash A\) - to zbiór zawierający wszystkie liczby nieparzyste oraz liczbę parzystą \(6\).

Rozpatrzmy przestrzeń wszystkich uczniów pewnej klasy.
Niech \(A\) - to zbiór dziewcząt tej klasy.
Wówczas \(A'\) - to zbiór chłopców tej klasy.

Poziom rozszerzony

I prawo de Morgana

Dopełnienie części wspólnej zbiorów \(A\) i \(B\) jest sumą dopełnień tych zbiorów: \[(A\cap B)' = A'\cup B'\]

II prawo de Morgana

Dopełnienie sumy zbiorów \(A\) i \(B\) jest częścią wspólną dopełnień tych zbiorów: \[(A\cup B)' = A'\cap B'\]

Powyższe prawa można łatwo uzasadnić rysując diagramy dla lewej i prawej strony równania. W poniższych przykładach wykażemy analogiczne zależności dla trzech zbiorów.

Narysuj diagram dla zbioru: \(A' \cup B' \cup C'\).

Sprawdzamy jak wygląda dopełnienie każdego zbioru oddzielnie: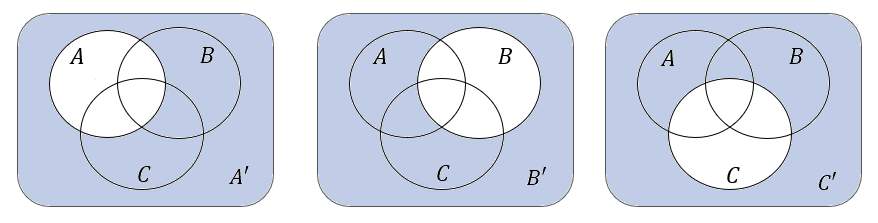

Gdy weźmiemy sumę tych dopełnień to otrzymamy:

Suma dopełnień \(A' \cup B' \cup C'\)

Zauważmy, że powyższy diagram przedstawia również dopełnienie części wspólnej tych zbiorów. Zatem uzasadniliśmy wzór: \[A' \cup B' \cup C' = (A\cap B \cap C)'\]

Uzasadnij, że: \((A\cup B \cup C)'= A'\cap B' \cap C'\).

Diagram dla lewej strony łatwo narysować:

Dopełnienie sumy zbiorów \((A\cup B \cup C)'\)

Teraz narysujemy diagram dla prawej strony.
Rysujemy dopełnienia każdego zbioru oddzielnie:

A następnie bierzemy część wspólną wszystkich trzech zamalowanych obszarów:

Część wspólna dopełnień zbiorów \(A'\cap B' \cap C'\)

Otrzymane diagramy wyglądają identycznie, zatem zachodzi: \[(A\cup B \cup C)'= A'\cap B' \cap C'\]

Ciekawostka

Takie diagramy, których użyliśmy do pokazania zależności między zbiorami, noszą nazwę diagramów Venna od nazwiska angielskiego matematyka Johna Venna (1834-1923).