Punkty A oraz B leżą na okręgu o środku S. Kąt środkowy ASB ma miarę 100°. Prosta l jest styczna do tego okręgu w punkcie A i tworzy z cięciwą AB okręgu kąt o mierze α (zobacz rysunek). Wtedy A. α =40° B. α =45° C. α =50° D. α =60°

Drukuj

Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(S\). Kąt środkowy \(ASB\) ma miarę \(100^\circ\). Prosta \(l\) jest styczna do tego okręgu w punkcie \(A\) i tworzy z cięciwą \(AB\) okręgu kąt o mierze \(\alpha\) (zobacz rysunek).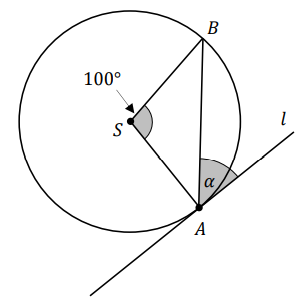

Wtedy

A.\( \alpha =40^\circ \)

B.\( \alpha =45^\circ \)

C.\( \alpha =50^\circ \)

D.\( \alpha =60^\circ \)

Strony z tym zadaniem

Matura 2022 sierpień Matura podstawowa - zbiór zadań - promienie, cięciwy i średnice w okręgu

Sąsiednie zadania

Zadanie 3717 Zadanie 3718

Zadanie 3719 (tu jesteś)

Zadanie 3720 Zadanie 3721