Zbiór zadań - okrąg i koło
Poziom podstawowy
Dane są okrąg o środku \(S\) oraz prosta \(k\) styczna do okręgu w punkcie \(A\). Odcinek \(AB\) jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą \(k\) a cięciwą \(AB\) jest równa \(50^\circ\). Punkt \(C\) leży na okręgu. Kąt \(\sphericalangle BCA\) jest ostry. Sytuację przedstawia rysunek poniżej. 

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Miara kąta \(\sphericalangle BCA\) jest równa A.\( 100^\circ \)
B.\( 80^\circ \)
C.\( 50^\circ \)
D.\( 40^\circ \)
Odcinek \(AB\) jest średnicą okręgu o środku w punkcie \(O\) i promieniu \(r = 8\) (zobacz rysunek). Cięciwa \(AC\) ma długość \(8\sqrt{3}\). 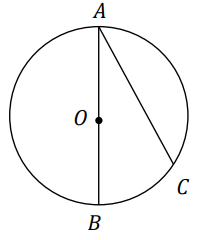

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta \(BAC\) jest równa A.\( 30^\circ \)
B.\( 45^\circ \)
C.\( 15^\circ \)
D.\( 60^\circ \)
Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(O\). Proste \(k\) i \(l\) są styczne do tego okręgu w punktach - odpowiednio - \(A\) i \(B\). Te proste przecinają się w punkcie \(S\) i tworzą kąt o mierze \(76^\circ\) (zobacz rysunek). 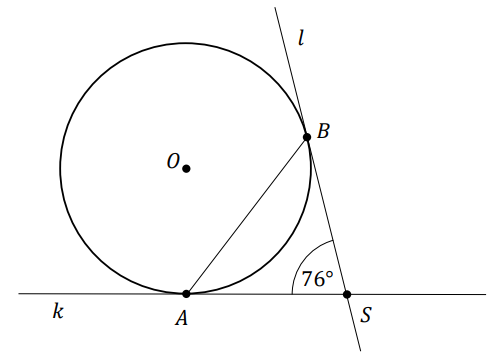

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta \(OBA\) jest równa A.\( 52^\circ \)
B.\( 26^\circ \)
C.\( 14^\circ \)
D.\( 38^\circ \)
Wierzchołki \(A\), \(B\), \(C\) czworokąta \(ABSC\) leżą na okręgu o środku \(S\). Kąt \(ABS\) ma miarę \(40^\circ\) (zobacz rysunek), a przekątna \(BC\) jest dwusieczną tego kąta. 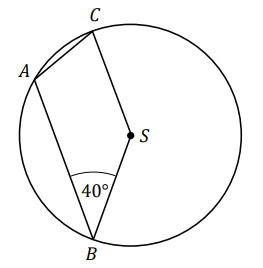 Miara kąta \(ASC\) jest równa
Miara kąta \(ASC\) jest równa
 Miara kąta \(ASC\) jest równa
Miara kąta \(ASC\) jest równa A.\( 30^\circ \)
B.\( 40^\circ \)
C.\( 50^\circ \)
D.\( 60^\circ \)
Punkty \(A\) oraz \(B\) leżą na okręgu o środku \(S\). Kąt środkowy \(ASB\) ma miarę \(100^\circ\). Prosta \(l\) jest styczna do tego okręgu w punkcie \(A\) i tworzy z cięciwą \(AB\) okręgu kąt o mierze \(\alpha\) (zobacz rysunek). 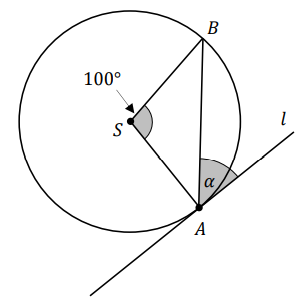 Wtedy
Wtedy
 Wtedy
Wtedy A.\( \alpha =40^\circ \)
B.\( \alpha =45^\circ \)
C.\( \alpha =50^\circ \)
D.\( \alpha =60^\circ \)
Dane są okrąg o środku \(S\) oraz prosta \(k\) styczna do okręgu w punkcie \(A\). Odcinek \(AB\) jest cięciwą tego okręgu. Miara kąta ostrego pomiędzy prostą \(k\) a cięciwą \(AB\) jest równa \(50^{\circ}\). Punkt \(C\) leży na okręgu. Kąt wpisany \(BCA\) jest ostry. Sytuację przedstawia rysunek poniżej. 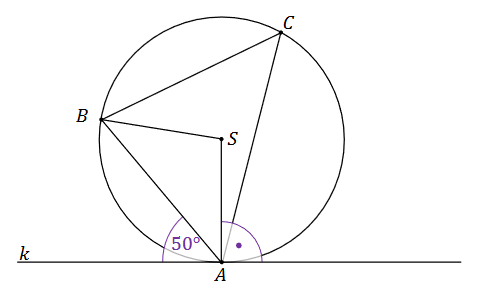

Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych.
Miara kąta wpisanego \(BCA\) jest równa A.\(100^{\circ}\)
B.\(80^{\circ}\)
C.\(50^{\circ}\)
D.\(40^{\circ}\)
Na rysunku zaznaczono kąt środkowy okręgu o mierze \(250^\circ \) oraz kąt prosty pod jakim przecinają się dwie cięciwy.  Zaznaczony kąt \(\alpha \) ma miarę
Zaznaczony kąt \(\alpha \) ma miarę
 Zaznaczony kąt \(\alpha \) ma miarę
Zaznaczony kąt \(\alpha \) ma miarę A.\( 30^\circ \)
B.\( 35^\circ \)
C.\( 40^\circ \)
D.\( 45^\circ \)
Punkty \(A, B, C\) i \(D\) leżą na okręgu o środku w punkcie \(O\). Cięciwy \(DB\) i \(AC\) przecinają się w punkcie \(E\), \(|\sphericalangle ACB|=55^\circ \) oraz \(|\sphericalangle AEB|=140^\circ \) (zobacz rysunek).  Miara kąta \(DAC\) jest równa
Miara kąta \(DAC\) jest równa
 Miara kąta \(DAC\) jest równa
Miara kąta \(DAC\) jest równa A.\( 45^\circ \)
B.\( 55^\circ \)
C.\( 70^\circ \)
D.\( 85^\circ \)
Prosta \(k\) jest styczna w punkcie \(A\) do okręgu o środku \(O\). Punkt \(B\) leży na tym okręgu i miara kąta \(AOB\) jest równa \(80^\circ \). Przez punkty \(O\) i \(B\) poprowadzono prostą, która przecina prostą \(k\) w punkcie \(C\) (zobacz rysunek). 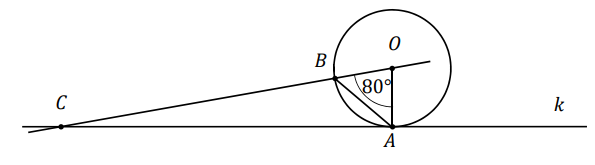 Miara kąta \(BAC\) jest równa
Miara kąta \(BAC\) jest równa
 Miara kąta \(BAC\) jest równa
Miara kąta \(BAC\) jest równa A.\( 10^\circ \)
B.\( 30^\circ \)
C.\( 40^\circ \)
D.\( 50^\circ \)
Punkty \(A,\ B,\ C\) leżą na okręgu o środku \(S\). Punkt \(D\) jest punktem przecięcia cięciwy \(AC\) i średnicy okręgu poprowadzonej z punktu \(B\). Miara kąta \(BSC\) jest równa \(\alpha \), a miara kąta \(ADB\) jest równa \(\gamma \) (zobacz rysunek).  Wtedy kąt \(ABD\) ma miarę
Wtedy kąt \(ABD\) ma miarę
 Wtedy kąt \(ABD\) ma miarę
Wtedy kąt \(ABD\) ma miarę A.\( \frac{\alpha }{2}+\gamma -180^\circ \)
B.\( 180^\circ -\frac{\alpha }{2}-\gamma \)
C.\( 180^\circ -\alpha -\gamma \)
D.\( \alpha +\gamma -180^\circ \)
Dany jest okrąg o środku w punkcie \(S\) i promieniu \(6\). Miara kąta wpisanego \(A C B\) jest równa \(60^{\circ}\) (zobacz rysunek). 

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość łuku \(AB\), na którym oparty jest kąt wpisany \(ACB\), jest równa A.\(2 \pi\)
B.\(4 \pi\)
C.\(6 \pi\)
D.\(12 \pi\)
Końce odcinka \(AB\) o długości \(9\) są środkami okręgów o promieniach \(6\) i \(4\) (zobacz rysunek).  Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
 Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość
Punkt \(C\) leży na odcinku \(AB\) i jest środkiem takiego okręgu, o promieniu większym od \(6\), że dwa dane okręgi są do niego wewnętrznie styczne. Promień okręgu o środku \(C\) ma długość A.\( 6{,}5 \)
B.\( 7{,}5 \)
C.\( 8{,}5 \)
D.\( 9{,}5 \)
W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość \(10\) i jest styczna do wewnętrznego okręgu (zobacz rysunek).  Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
 Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.Na trójkącie o bokach długości \(\sqrt{7}, \sqrt{8}, \sqrt{15}\) opisano okrąg. Oblicz promień tego okręgu.
Dwa okręgi o promieniach \(r\) i \(R\) są styczne zewnętrznie i są styczne do wspólnej prostej w punktach \(A\) i \(B\) (zobacz rysunek). Oblicz wartość iloczynu \(rR\), jeżeli wiadomo, że odcinek \(AB\) ma długość \(5\). 

Do okręgu o środku \(O\) poprowadzono z zewnętrznego punktu \(P\) dwie styczne przecinające się w \(P\) pod kątem \(50^\circ \) (zobacz rysunek). Punktami styczności są, odpowiednio, punkty \(A\) i \(B\).  Kąt \(AOB\) ma miarę
Kąt \(AOB\) ma miarę
 Kąt \(AOB\) ma miarę
Kąt \(AOB\) ma miarę A.\( 90^\circ \)
B.\( 120^\circ \)
C.\( 130^\circ \)
D.\( 150^\circ \)
Dany jest okrąg o środku w punkcie \(S\) i promieniu \(r\). Na przedłużeniu cięciwy \(AB\) poza punkt \(B\) odłożono odcinek \(BC\) równy promieniowi danego okręgu. Przez punkty \(C\) i \(S\) poprowadzono prostą. Prosta \(CS\) przecina dany okrąg w punktach \(D\) i \(E\) (zobacz rysunek). Wykaż, że jeżeli miara kąta \(ACS\) jest równa \(\alpha\), to miara kąta \(ASD\) jest równa \(3\alpha\). 

Pole figury \(F_1\) złożonej z dwóch stycznych zewnętrznie kół o promieniach \(1\) i \(3\) jest równe polu figury \(F_2\) złożonej z dwóch stycznych zewnętrznie kół o promieniach długości \(r\) (zobacz rysunek). 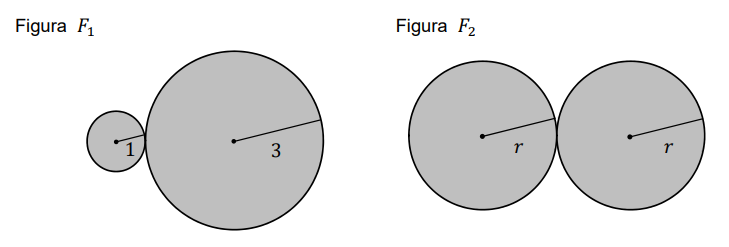 Długość \(r\) promienia jest równa
Długość \(r\) promienia jest równa
 Długość \(r\) promienia jest równa
Długość \(r\) promienia jest równa A.\( \sqrt{3} \)
B.\( 2 \)
C.\( \sqrt{5} \)
D.\( 3 \)
Punkty \(A,\ B,\ P\) leżą na okręgu o środku \(S\) i promieniu \(6\). Czworokąt \(ASBP\) jest rombem, w którym kąt ostry \(PAS\) ma miarę \(60^\circ \) (zobacz rysunek). 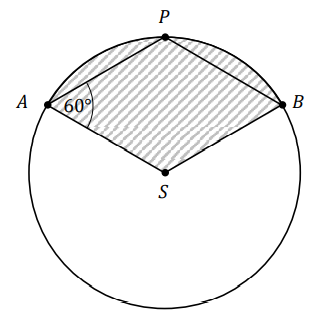 Pole zakreskowanej na rysunku figury jest równe
Pole zakreskowanej na rysunku figury jest równe
 Pole zakreskowanej na rysunku figury jest równe
Pole zakreskowanej na rysunku figury jest równe A.\( 6\pi \)
B.\( 9\pi \)
C.\( 10\pi \)
D.\( 12\pi \)
Dwa okręgi o promieniach \(r = 2\) i \(R = 6\) są styczne zewnętrznie i są styczne do wspólnej prostej \(k\). Wykaż, że prosta \(l\) przechodząca przez środki \(S\) i \(P\) tych okręgów przecina prostą \(k\) pod kątem \(\alpha = 30^\circ \) (zobacz rysunek). 

Środek okręgu leży w odległości \(10\) cm od cięciwy tego okręgu. Długość tej cięciwy jest o \(22\) cm większa od promienia tego okręgu. Oblicz promień tego okręgu.
W kwadrat o boku długości \(1\) wpisano półokrąg i narysowano do niego odcinek styczny. Oblicz długość tego odcinka. 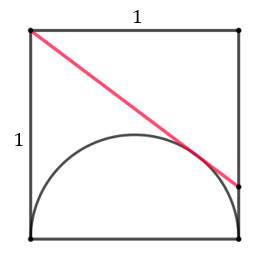

Tematy nadrzędne