Do okręgu o środku w punkcie \(O\) poprowadzono z trzech punktów \(A\), \(B\) i \(C\) leżących na okręgu styczne, które przecięły się w punktach \(D\), \(E\) i \(F\) (zobacz rysunek). Wykaż, że jeżeli \(|AF|=x\), to obwód trójkąta \(DEF\) jest równy \(2x\). 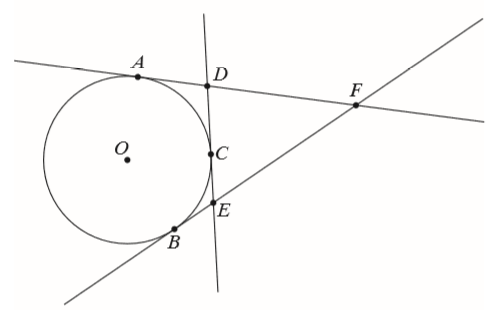

Strony z tym zadaniem
Matura 2018 listopadSąsiednie zadania
Zadanie 2795Zadanie 2796Zadanie 2797 (tu jesteś)
Zadanie 2798Zadanie 2799