Odcinek \(CD\) jest wysokością trójkąta \(ABC\), w któym \(|AD|=|CD|=\frac{1}{2}|BC|\) (zobacz rysunek). Okrąg o środku \(C\) i promieniu \(CD\) jest styczny do prostej \(AB\). Okrąg ten przecina boki \(AC\) i \(BC\) trójkąta odpowiednio w punktach \(K\) i \(L\).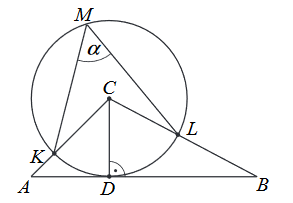 
Zaznaczony na rysunku kąt \(\alpha \) wpisany w okrąg jest równy
Zaznaczony na rysunku kąt \(\alpha \) wpisany w okrąg jest równy A.\( 37{,}5^\circ \)
B.\( 45^\circ \)
C.\( 52{,}5^\circ \)
D.\( 60^\circ \)
Strony z tym zadaniem
Matura 2017 maj PRSąsiednie zadania
Zadanie 2406Zadanie 2407Zadanie 2408 (tu jesteś)
Zadanie 2409Zadanie 2410