Matura 2017 maj PR

Oblicz \(\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)^2\).

Nieskończony ciąg liczbowy jest określony wzorem \(a_n=\frac{(n^2-10n)(2-3n)}{2n^3+n^2+3}\) dla \(n\ge 1\). Wtedy

Odcinek \(CD\) jest wysokością trójkąta \(ABC\), w któym \(|AD|=|CD|=\frac{1}{2}|BC|\) (zobacz rysunek). Okrąg o środku \(C\) i promieniu \(CD\) jest styczny do prostej \(AB\). Okrąg ten przecina boki \(AC\) i \(BC\) trójkąta odpowiednio w punktach \(K\) i \(L\). 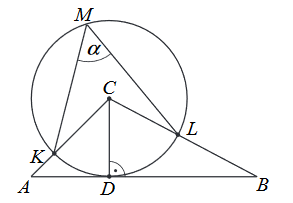Zaznaczony na rysunku kąt \(\alpha \) wpisany w okrąg jest równy

Dane są punkt \(B=(-4,7)\) i wektor \(\vec{u}=[-3,5]\). Punkt \(A\), taki, że \(\vec{AB}=-3\vec{u}\), ma współrzędne

Reszta z dzielenia wielomianu \(W(x)=x^3-2x^2+ax+\frac{3}{4}\) przez dwumian \(x-2\) jest równa \(1\). Oblicz wartość współczynnika \(a\).
W poniższe kratki wpisz kolejno trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x-1}{x^2+1}\) dla każdej liczby rzeczywistej \(x\). Wyznacz równanie stycznej do wykresu tej funkcji w punkcie \(P=(1,0)\).

Udowodnij, że dla dowolnych różnych liczb rzeczywistych \(x\), \(y\) prawdziwa jest nierówność: \[x^2y^2+2x^2+2y^2-8xy+4\gt 0\]

W trójkącie ostrokątnym \(ABC\) bok \(AB\) ma długość \(c\), długość boku \(BC\) jest równa \(a\) oraz \(|\sphericalangle ABC|=\beta \). Dwusieczna kąta \(ABC\) przecina bok \(AC\) trójkąta w punkcie \(E\). Wykaż, że długość odcinka \(BE\) jest równa \(\frac{2ac \cdot \cos \frac{\beta }{2}}{a+c}\).

W czworościanie, którego wszystkie krawędzie maja taką samą długość \(6\), umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna \(\pi\), równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej \(\frac{8}{27}\) objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka \(S\) kuli od płaszczyzny \(\pi\), tj. długość najkrótszego spośród odcinków \(SP\), gdzie \(P\) jest punktem płaszczyzny \(\pi\).

Rozwiąż równanie \(\cos 2x+3\cos x=-2\) w przedziale \(\langle 0,2\pi \rangle \).

W pudełku znajduje się \(8\) piłeczek oznaczonych kolejnymi liczbami naturalnymi od \(1\) do \(8\). Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez \(4\). Wynik podaj w postaci ułamka zwykłego.

Wyznacz wszystkie wartości parametru \(m\), dla których równianie \[4x^2-6mx+(2m+3)(m-3)=0\] ma dwa różne rozwiązania rzeczywiste \(x_1\) i \(x_2\), przy czym \(x_1\lt x_2\), spełniające warunek \[(4x_1-4x_2-1)(4x_1-4x_2+1)\lt 0 .\]

Wyznacz równanie okręgu przechodzącego przez punkty \(A=(-5,3)\) i \(B=(0,6)\), którego środek leży na prostej o równaniu \(x-3y+1=0\).

Liczby \(a, b, c\) są - odpowiednio - pierwszym drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa \(27\). Ciąg \((a-2,b,2c+1)\) jest geometryczny. Wyznacz liczby \(a, b, c\).

Rozpatrujemy wszystkie walce o danym polu powierzchni całkowitej \(P\). Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.