Wzory na pole trójkąta
Pole trójkąta można obliczyć na wiele różnych sposobów. Wszystko zależy od tego jakimi danymi dysponujemy.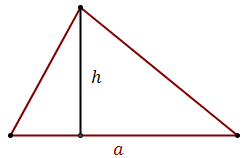 
\[ P = \frac{1}{2}ah\] gdzie: 
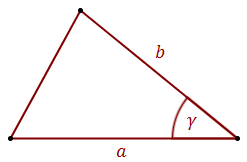\[P=\frac{1}{2}ab\sin \gamma \] gdzie: 
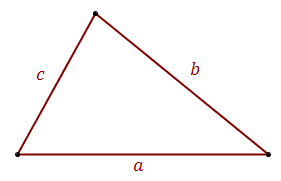\[ P=\sqrt{p(p-a)(p-b)(p-c)} \] gdzie: 
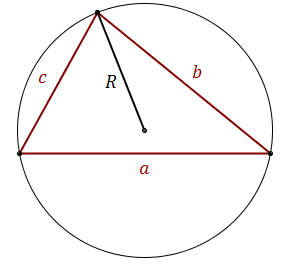\[ P=\frac{abc}{4R} \] gdzie: 
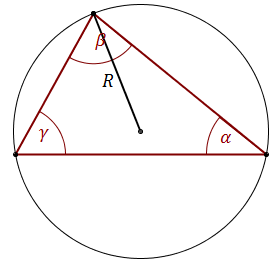\[ P=2R^2\sin \alpha \sin \beta \sin \gamma \] gdzie: 
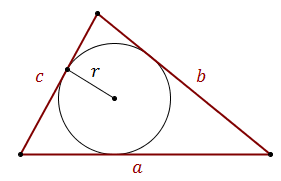\[ P=r\cdot \frac{a+b+c}{2} \] gdzie:
Wzór 1
\[ P = \frac{1}{2}ah\] gdzie: \(a\) - długość jednego boku trójkąta
\(h\) - długość wysokości opuszczonej na bok \(a\)
\(h\) - długość wysokości opuszczonej na bok \(a\)
Wzór 2
\[P=\frac{1}{2}ab\sin \gamma \] gdzie: \(a\), \(b\) - długości dwóch boków trójkąta
\(\gamma \) - kąt między bokami \(a\) i \(b\)
\(\gamma \) - kąt między bokami \(a\) i \(b\)
Wzór 3
\[ P=\sqrt{p(p-a)(p-b)(p-c)} \] gdzie: \(a\), \(b\), \(c\) - długości boków trójkąta
\(p\) - połowa obwodu trójkąta, czyli \(p=\frac{a+b+c}{2}\)
\(p\) - połowa obwodu trójkąta, czyli \(p=\frac{a+b+c}{2}\)
Wzór 4
\[ P=\frac{abc}{4R} \] gdzie: \(a\), \(b\), \(c\) - długości boków trójkąta
\(R\) - długość promienia okręgu opisanego na trójkącie
\(R\) - długość promienia okręgu opisanego na trójkącie
Wzór 5
\[ P=2R^2\sin \alpha \sin \beta \sin \gamma \] gdzie: \(\alpha \), \(\beta \), \(\gamma \) - kąty wewnętrzne trójkąta
\(R\) - długość promienia okręgu opisanego na trójkącie
\(R\) - długość promienia okręgu opisanego na trójkącie
Wzór 6
\[ P=r\cdot \frac{a+b+c}{2} \] gdzie: \(r\) - długość promienia okręgu wpisanego w trójkąt
Tematy nadrzędne i sąsiednie