Wykres wartości bezwzględnej

Drukuj

Poziom podstawowy

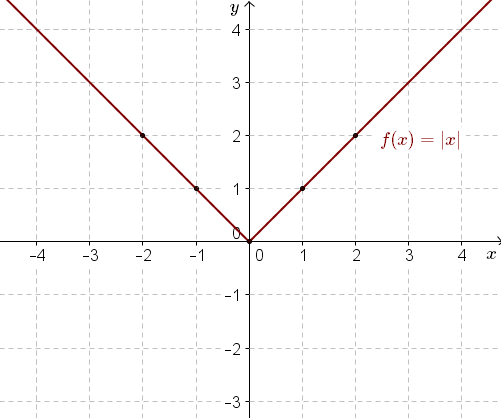
Narysujemy najpierw wykres funkcji \[f(x)=|x|\] Możemy dla ułatwienia sporządzić odpowiednią tabelkę:

\(x\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)
\(f(x)=\|x\|\)	\(2\)	\(1\)	\(0\)	\(1\)	\(2\)

Teraz zaznaczymy wyznaczone punkty w układzie współrzędnych i narysujemy wykres:

Bardzo podobnie wyglądają wykresy funkcji \(f(x) = |ax|\), gdzie \(a\) to dowolna liczba, np: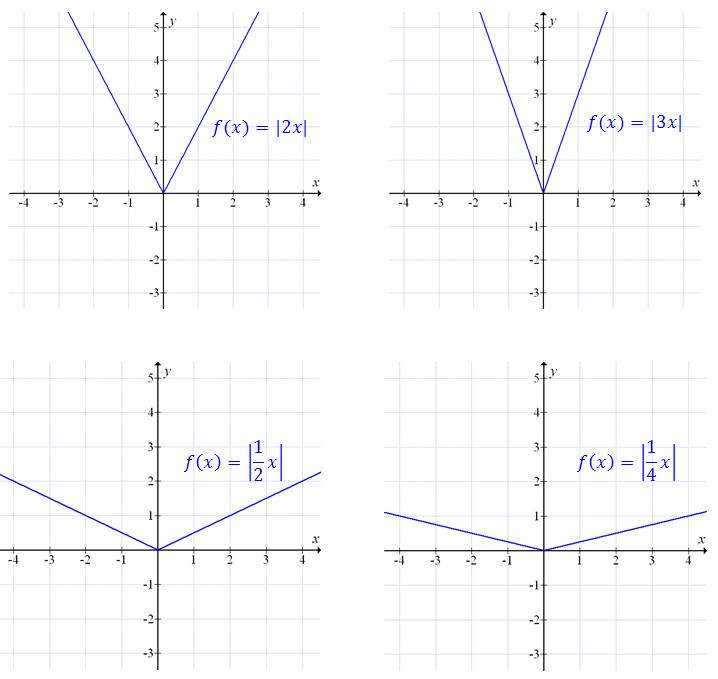

Żeby narysować wykres funkcji \[f(x) = a|x + b| + c\] to należy przesunąć wykres funkcji \(f(x) = a|x|\) o wektor \([-b, c]\).

Narysujemy wykres funkcji \(f(x) = |x + 3| + 2\).
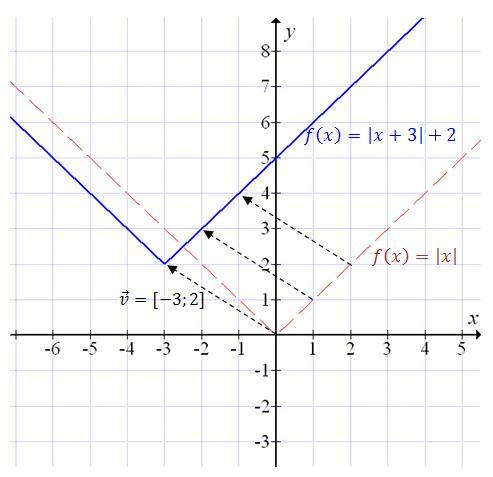
Musimy zatem przesunąć wykres funkcji \(f(x) = |x|\) o wektor \([-3, 2]\).

Wykres dowolnej funkcji możesz narysować korzystając z programu do rysowania wykresów funkcji.

Poziom rozszerzony

Na rysunku przedstawiono fragment wykresu funkcji \(y = f(x)\), który jest złożony z dwóch półprostych \(AD\) i \(CE\) oraz dwóch odcinków \(AB\) i \(BC\), gdzie \(A = (-1, 0)\), \(B = (1, 2)\), \(C = (3, 0)\), \(D = (-4, 3)\), \(E = (6, 3)\).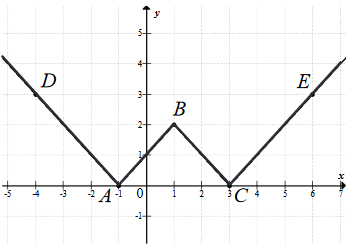

Wzór funkcji \(f\) to

A.\( f(x) = |x + 1| + |x - 1| \)

B.\( f(x) = ||x - 1| - 2| \)

C.\( f(x) = ||x - 1| + 2| \)

D.\( f(x) = |x - 1| + 2 \)

\(f(x) = ||x - 1| - 2|\)