Wykres funkcji sinus

Drukuj

Poziom rozszerzony

Funkcja sinus wyraża się wzorem: \[f(x)=\sin x\] Jej wykresem jest sinusoida:

Sinus jest funkcją okresową o okresie \(2\pi \).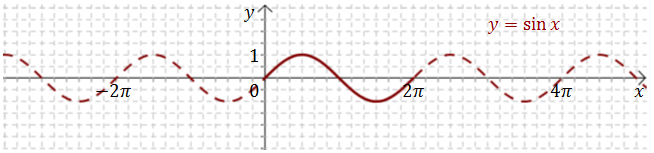

Fragment wykresu narysowany linią ciągłą pokazuje jeden pełny okres sinusa, który powtarza się nieskończenie wiele razy.

Żeby narysować wykres sinusa, to wystarczy znać wartości funkcji dla kątów ostrych, czyli z przedziału \(\left \langle 0, \frac{\pi }{2} \right \rangle\). W kolejnych przedziałach można potem odpowiednio powielać otrzymany fragment wykresu (np. odbijając go symetrycznie).

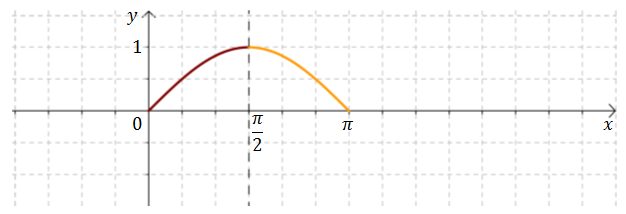
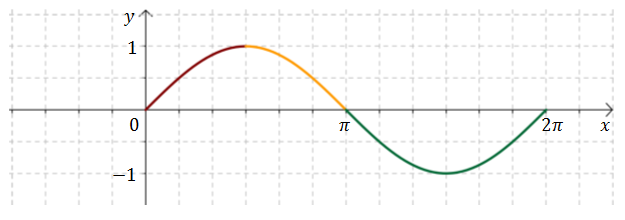Przyjrzyjmy się teraz dokładniej wykresowi sinusa na przedziale \(\left \langle 0, \frac{\pi }{2} \right \rangle\).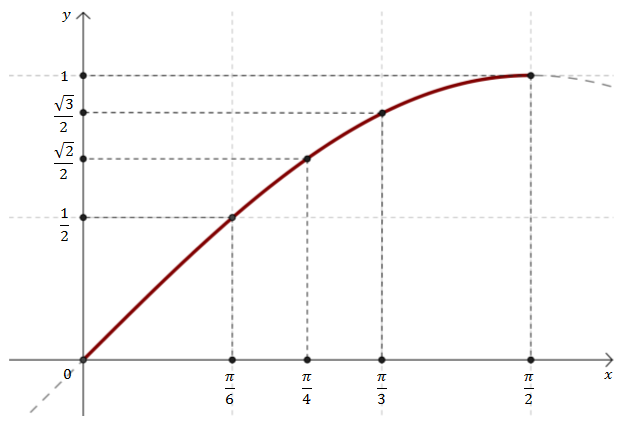

Znając wykres sinusa możemy bardzo łatwo przypominać sobie wartości trygonometryczne różnych kątów.
Szczególnie łatwo możemy odczytać, że \(\sin \frac{\pi }{6} = \frac{1}{2}\).

Zobaczmy teraz jak można na podstawie wykresu odczytać wartości sinusa dla kątów rozwartych.

Oblicz \(\sin 150^\circ \).

Zaczynamy od zamienienia stopni na radiany: \[150^\circ = \frac{5\pi }{6}\] Teraz zaznaczamy na wykresie sinusa punkt o argumencie \(\frac{5\pi }{6}\).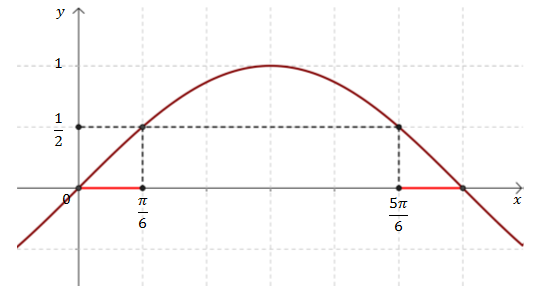

Z wykresu odczytujemy, że: \[\sin \frac{5\pi}{6}=\sin \frac{\pi }{6}=\frac{1}{2}\]

Oblicz \(\sin \frac{5\pi }{4}\).

Zaznaczamy na wykresie funkcji sinus punkt o argumencie \(x = \frac{5\pi }{4}\).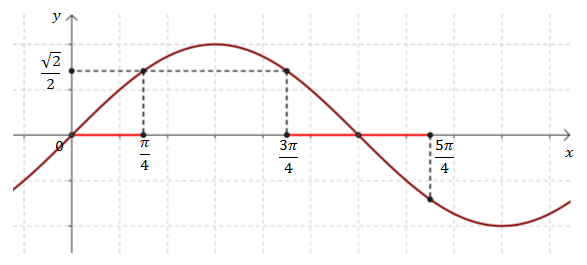

Z wykresu odczytujemy, że: \[\sin \frac{5\pi}{4}=-\sin \frac{3\pi}{4}=-\sin \frac{\pi }{4}=-\frac{\sqrt{2}}{2}\]