Wykres funkcji cosinus
Funkcja cosinus wyraża się wzorem: \[f(x)=\cos x\] Jej wykresem jest cosinusoida: 
Cosinus jest funkcją okresową o okresie \(2\pi \). Na poniższym wykresie linią ciągłą zaznaczono jeden pełny okres cosinusa. 
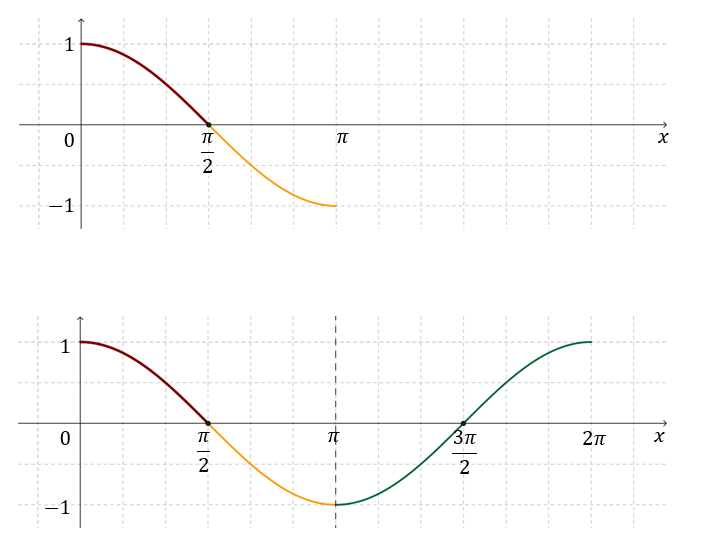Przyjrzyjmy się teraz dokładniej wykresowi sinusa na przedziale \(\left \langle 0, \frac{\pi }{2} \right \rangle\). 
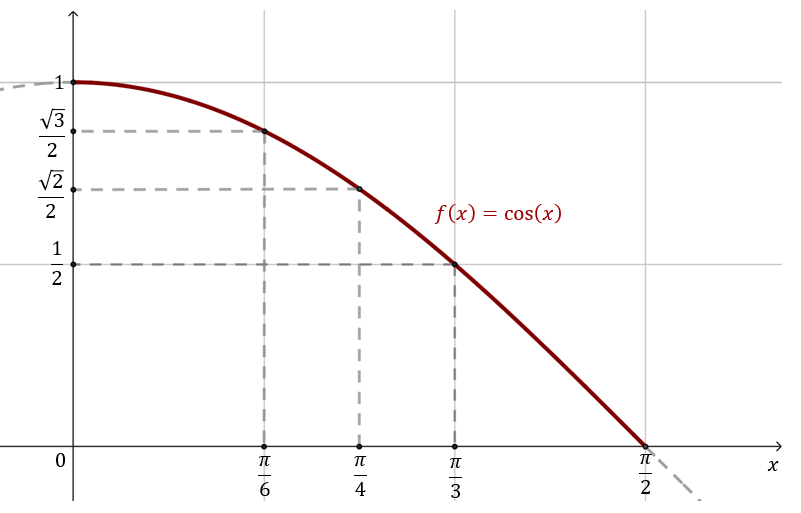Znając wykres cosinusa można bardzo łatwo przypominać sobie wartości funkcji trygonometrycznych dla różnych kątów, np: \[\cos \frac{\pi }{3} = \frac{1}{2}\]
Cosinus jest funkcją okresową o okresie \(2\pi \). Na poniższym wykresie linią ciągłą zaznaczono jeden pełny okres cosinusa. Żeby narysować wykres cosinusa, to wystarczy znać jego wartości dla kątów z przedziału \(\left \langle 0, \frac{\pi }{2} \right \rangle\). Następnie w kolejnych przedziałach można powielać otrzymany fragment wykresu (np. odbijając go symetrycznie).
Przyjrzyjmy się teraz dokładniej wykresowi sinusa na przedziale \(\left \langle 0, \frac{\pi }{2} \right \rangle\). Znając wykres cosinusa można bardzo łatwo przypominać sobie wartości funkcji trygonometrycznych dla różnych kątów, np: \[\cos \frac{\pi }{3} = \frac{1}{2}\] Zobaczmy teraz jak można na podstawie wykresu odczytać wartości cosinusa dla kątów rozwartych.
Oblicz \(\cos 120^\circ \).
Zaczynamy od zamienienia stopni na radiany: \[120^\circ = 4\cdot \frac{\pi }{6}=\frac{2\pi}{3}\] Teraz zaznaczamy na wykresie cosinusa punkt o argumencie \(\frac{2\pi }{3}\).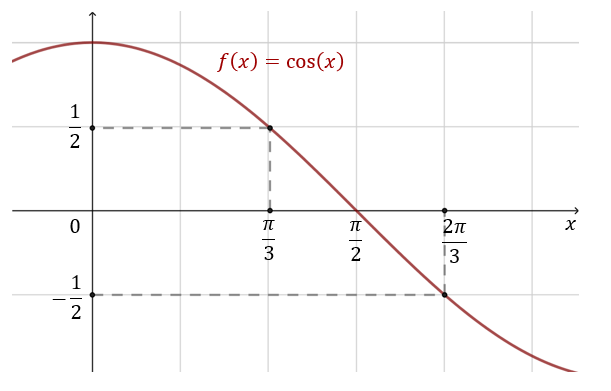 
Z wykresu odczytujemy, że: \[\cos \frac{2\pi}{3}=-\cos \frac{\pi }{3}=-\frac{1}{2}\]
Z wykresu odczytujemy, że: \[\cos \frac{2\pi}{3}=-\cos \frac{\pi }{3}=-\frac{1}{2}\] Oblicz \(\cos \frac{7\pi }{6}\).
Zaznaczamy na wykresie funkcji cosinus punkt o argumencie \(x = \frac{7\pi }{6}\).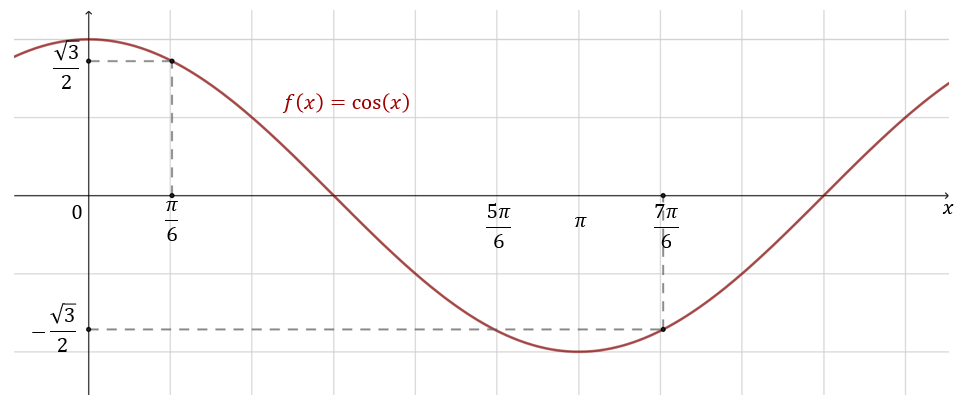 
Z wykresu odczytujemy, że: \[\cos \frac{7\pi}{6}=\cos \frac{5\pi}{6}=-\cos \frac{\pi }{6}=-\frac{\sqrt{3}}{2}\]
Z wykresu odczytujemy, że: \[\cos \frac{7\pi}{6}=\cos \frac{5\pi}{6}=-\cos \frac{\pi }{6}=-\frac{\sqrt{3}}{2}\] Tematy nadrzędne i sąsiednie