Walec
Poziom podstawowy
Walec - to bryła obrotowa powstała przez obrót prostokąta wokół prostej zawierającej jeden z jego boków. Prostą tę nazywamy osią walca.  Przekrojem osiowym walca jest prostokąt.
Przekrojem osiowym walca jest prostokąt.Podstawami walca są koła. Dowolny odcinek łączący podstawy i prostopadły do nich, nazywamy wysokością walca. Wysokość, która łączy brzegi podstaw nazywana jest też tworzącą walca.
Wzory
Objętość walca: \[V=P_p\cdot h=\pi r^2h\] Pole podstawy walca: \[P_p=\pi r^2\] Pole powierzchni bocznej walca: \[P_b=2\pi rh\] Pole powierzchni całkowitej walca: \[P_c=2P_p+P_b=2\pi r^2+2\pi rh=2\pi r(r+h)\]
Pole powierzchni bocznej walca, którego podstawa ma średnicę \(4\) jest równe \(8\pi \). Wysokość tego walca jest równa
A.\( 8 \)
B.\( 4 \)
C.\( 2 \)
D.\( \frac{1}{2} \)
Przekrój osiowy walca jest kwadratem o boku \(a\). Jeżeli \(r\) oznacza promień podstawy walca, \(h\) oznacza wysokość walca, to
A.\( r+h=a \)
B.\( h-r=\frac{a}{2} \)
C.\( r-h=\frac{a}{2} \)
D.\( r^2+h^2=a^2 \)
Przekrój osiowy walca jest kwadratem o boku długości \(6\). Objętość tego walca jest równa 

A.\( 18\pi \)
B.\( 54\pi \)
C.\( 108\pi \)
D.\( 216\pi \)
Objętość walca o wysokości \(8\) jest równa \(72\pi\). Promień podstawy tego walca jest równy
A.\( 9 \)
B.\( 8 \)
C.\( 6 \)
D.\( 3 \)
Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa \( 24\pi \). Zatem promień podstawy tego walca ma długość
A.\(4 \)
B.\(8 \)
C.\(2 \)
D.\(6 \)
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości \( 4 \), jest równe 

A.\(256\pi \)
B.\(128\pi \)
C.\(48\pi \)
D.\(24\pi \)
Prostokąt o bokach długości \(2\) i \(4\) obracamy wokół krótszego boku. Ile wynosi pole powierzchni całkowitej tak otrzymanej bryły?
A.\( 16\pi \)
B.\( 24\pi \)
C.\( 32\pi \)
D.\( 48\pi \)
Przekątna przekroju osiowego walca, którego promień podstawy jest równy \(4\) i wysokość jest równa \(6,\) ma długość
A.\( \sqrt{10} \)
B.\( \sqrt{20} \)
C.\( \sqrt{52} \)
D.\( 10 \)
Dany jest walec, w którym promień podstawy jest równy \(r\), a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A.\( 2\pi r^3 \)
B.\( 4\pi r^3 \)
C.\( \pi r^2(r+2) \)
D.\( \pi r^2(r-2) \)
Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa \(27\pi\). Wynika stąd, że promień podstawy tego walca jest równy
A.\( 9 \)
B.\( 6 \)
C.\( 3 \)
D.\( 2 \)
Przekrój osiowy walca jest kwadratem o boku długości \(6\). Objętość tego walca jest równa 

A.\( 108\pi \)
B.\( 54\pi \)
C.\( 36\pi \)
D.\( 27\pi \)
Promień \(AS\) podstawy walca jest równy wysokości \(OS\) tego walca. Sinus kąta \(OAS\) (zobacz rysunek) jest równy 

A.\( \frac{1}{2} \)
B.\( \frac{\sqrt{2}}{2} \)
C.\( \frac{\sqrt{3}}{2} \)
D.\( 1 \)
Pole powierzchni bocznej walca jest równe \(16\pi\), a promień jego podstawy ma długość \(2\). Wysokość tego walca jest równa
A.\( 4 \)
B.\( 8 \)
C.\( 4\pi \)
D.\( 8\pi \)
Przekrój osiowy walca jest kwadratem o przekątnej \(10\sqrt{2}\). Pole powierzchni bocznej tego walca jest równe
A.\( 50\pi \)
B.\( 100\pi \)
C.\( 200\pi \)
D.\( 250\pi \)
Przekrojem osiowym walca jest kwadrat o przekątnej długości \(12\). Objętość tego walca jest zatem równa
A.\( 36\pi\sqrt{2} \)
B.\( 108\pi\sqrt{2} \)
C.\( 54\pi \)
D.\( 108\pi \)
Przekątna przekroju osiowego walca jest równa \(4\). Przekątna ta tworzy z bokiem odpowiadającym wysokości kąt \(30^\circ \). Objętość walca wynosi
A.\( 2\sqrt{3}\pi \)
B.\( 3\sqrt{2}\pi \)
C.\( 8\sqrt{3}\pi \)
D.\( \frac{8\sqrt{3}\pi}{3} \)
Przekątna przekroju osiowego walca jest równa \(12\ \text{cm}\). Przekątna ta tworzy z bokiem odpowiadającym wysokości kąt \(36^\circ \). Oblicz pole powierzchni całkowitej i objętość bryły.
Wysokość walca jest równa 10 cm . Kąt między przekątnymi przekroju osiowego, leżący naprzeciw wysokości walca ma miarę \(120^{\circ}\). Oblicz objętość tego walca.
Poziom rozszerzony
Przekrojem osiowym walca jest prostokąt \(A B C D\). Dlugości boków \(A B\) i \(B C\) oraz przekątnej \(A C\) są kolejnymi wyrazami ciągu geometrycznego. Oblicz stosunek pola powierzchni bocznej tego walca do pola jego podstawy (rozpatrz dwa przypadki).
Tematy nadrzędne i sąsiednie
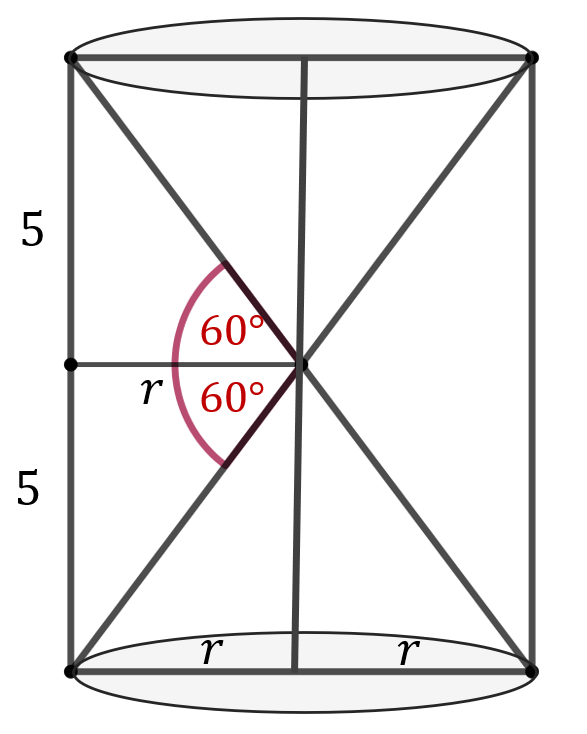 Z trójkąta prostokątnego o przyprostokątnych \(r\) oraz \(5\) mamy: \[\frac{5}{r}=\operatorname{tg} 60^\circ \\[6pt] \frac{5}{r}=\sqrt{3}\\[6pt] r=\frac{5}{\sqrt{3}} \] Zatem objętość walca wynosi: \[ V = \pi r^2 h = \pi \cdot \frac{25}{3} \cdot 10 = \frac{250\pi}{3}\, \text{cm}^3. \]
Z trójkąta prostokątnego o przyprostokątnych \(r\) oraz \(5\) mamy: \[\frac{5}{r}=\operatorname{tg} 60^\circ \\[6pt] \frac{5}{r}=\sqrt{3}\\[6pt] r=\frac{5}{\sqrt{3}} \] Zatem objętość walca wynosi: \[ V = \pi r^2 h = \pi \cdot \frac{25}{3} \cdot 10 = \frac{250\pi}{3}\, \text{cm}^3. \]