Stożek
Poziom podstawowy
Stożek - to bryła obrotowa otrzymana przez obrót trójkąta prostokątnego wokół prostej zawierającej jedną z jego przyprostokątnych. Prostą tę nazywamy osią stożka. 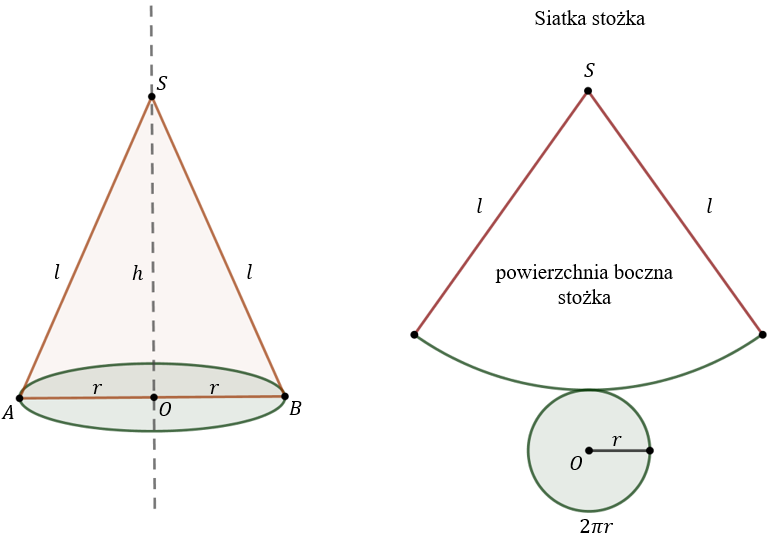 Na powyższym rysunku stożek został otrzymany przez obrót trójkąta \(AOS\) wokół prostej \(OS\).
Na powyższym rysunku stożek został otrzymany przez obrót trójkąta \(AOS\) wokół prostej \(OS\).Podstawą stożka jest koło o środku w punkcie \(O\) i promieniu \(r\).
Przekrojem osiowym stożka jest trójkąt równoramienny \(ABS\).
Wysokością \(h\) stożka jest odcinek \(OS\) łączący wierzchołek stożka \(S\) ze środkiem podstawy \(O\).
Tworzącą \(l\) stożka jest dowolny odcinek łączący wierzchołek stożka z brzegiem podstawy (np. odcinek \(AS\)).
Wzory
Objętość stożka: \[V=\frac{1}{3}P_p\cdot h=\frac{\pi r^2h}{3}\] Pole podstawy stożka: \[P_p=\pi r^2\] Pole powierzchni bocznej stożka: \[P_b=\pi rl\] Pole powierzchni całkowitej stożka: \[P_c=\pi r^2+\pi rl=\pi r(r+l)\]Pole powierzchni bocznej stożka o wysokości \(4\) i promieniu podstawy \(3\) jest równe
A.\( 9\pi \)
B.\( 12\pi \)
C.\( 15\pi \)
D.\( 16\pi \)
Jeśli średnica podstawy stożka jest równa \(12\), a wysokość stożka \(8\), to kąt \(\alpha\) między wysokością stożka, a jego tworzącą jest taki, że:
A.\( \operatorname{tg} \alpha =\frac{12}{8} \)
B.\( \operatorname{tg} \alpha =\frac{8}{12} \)
C.\( \operatorname{tg} \alpha =\frac{6}{8} \)
D.\( \operatorname{tg} \alpha =\frac{8}{6} \)
Przekrój osiowy stożka jest trójkątem równobocznym o boku \(a\). Objętość tego stożka wyraża się wzorem
A.\( \frac{\sqrt{3}}{6}\pi a^3 \)
B.\( \frac{\sqrt{3}}{8}\pi a^3 \)
C.\( \frac{\sqrt{3}}{12}\pi a^3 \)
D.\( \frac{\sqrt{3}}{24}\pi a^3 \)
Trójkąt prostokątny o przyprostokątnych \(4\) i \(6\) obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa
A.\( 96\pi \)
B.\( 48\pi \)
C.\( 32\pi \)
D.\( 8\pi \)
Tworząca stożka ma długość \(4\) i jest nachylona do płaszczyzny podstawy pod kątem \(60^\circ \). Objętość tego stożka jest równa
A.\( \frac{8\sqrt{3}\pi }{3} \)
B.\( \frac{10\sqrt{3}\pi }{3} \)
C.\( 3\sqrt{3}\pi \)
D.\( 16 \)
Tworząca stożka ma długość \( 4 \) i jest nachylona do płaszczyzny podstawy pod kątem \( 45^\circ \). Wysokość tego stożka jest równa
A.\(2\sqrt{2} \)
B.\(16\pi \)
C.\(4\sqrt{2} \)
D.\(8\pi \)
Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych \(13\) i \(15\) wokół dłuższej przyprostokątnej. Promień podstawy tego stożka jest równy
A.\( 15 \)
B.\( 13 \)
C.\( 7{,}5 \)
D.\( 6{,}5 \)
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości \(6\). Pole powierzchni bocznej tego stożka jest równe: 

A.\( 12\pi \)
B.\( 18\pi \)
C.\( 27\pi \)
D.\( 36\pi \)
Tworząca stożka jest o \(2\) dłuższa od promienia podstawy. Pole powierzchni bocznej tego stożka jest równe \(15\pi \). Tworząca stożka ma zatem długość
A.\( 1 \)
B.\( 5 \)
C.\( 3 \)
D.\( 15 \)
Wysokość stożka jest równa 15 cm, a promień podstawy 4 cm. Objętość stożka jest równa
A.\( 60\pi \) cm3
B.\( 80\pi \) cm3
C.\( 100\pi \) cm3
D.\( 125\pi \) cm3
Objętość stożka jest równa \(24\pi \) cm3, a promień podstawy \(6\) cm. Wysokość stożka jest równa
A.\( 2 \) cm
B.\( 4 \) cm
C.\( 6 \) cm
D.\( 8 \) cm
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu \(12\) cm. Podstawa tego stożka jest kołem o promieniu
A.\( 12 \) cm
B.\( 6 \) cm
C.\( 3 \) cm
D.\( 1 \) cm
Objętość stożka o wysokości \(8\) i średnicy podstawy \(12\) jest równa
A.\( 124\pi \)
B.\( 96\pi \)
C.\( 64\pi \)
D.\( 32\pi \)
Objętość stożka o wysokości \(h\) i promieniu podstawy trzy razy mniejszym od wysokości jest równa
A.\( \frac{1}{9}\pi h^2 \)
B.\( \frac{1}{27}\pi h^2 \)
C.\( \frac{1}{9}\pi h^3 \)
D.\( \frac{1}{27}\pi h^3 \)
Tworząca stożka ma długość \(l\), a promień jego podstawy jest równy \(r\). 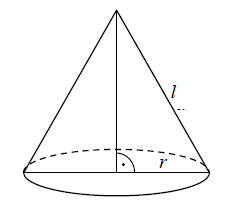 Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas
Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas
 Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas
Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas A.\( r=\frac{1}{6}l \)
B.\( r=\frac{1}{4}l \)
C.\( r=\frac{1}{3}l \)
D.\( r=\frac{1}{2}l \)
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości \(6\). Objętość tego stożka jest równa
A.\( 6\pi \)
B.\( 18\pi \)
C.\( 9\pi\sqrt{3} \)
D.\( 27\pi\sqrt{3} \)
Dany jest trójkąt prostokątny o długościach boków \(a, b, c\), gdzie \(a \lt b \lt c\). Obracając ten trójkąt wokół prostej zawierającej dłuższą przyprostokątną o kąt \(360^\circ \) otrzymujemy bryłę, której objętość jest równa
A.\( V=\frac{1}{3}a^2b\pi \)
B.\( V=a^2b\pi \)
C.\( V=\frac{1}{3}b^2a\pi \)
D.\( V=a^2\pi +\pi ac \)
Kula o promieniu \(5\) cm i stożek o promieniu podstawy \(10\) cm mają równe objętości. Wysokość stożka jest równa
A.\( \frac{25}{\pi } \) cm
B.\( 10 \) cm
C.\( \frac{10}{\pi } \) cm
D.\( 5 \) cm
Jeżeli wysokość stożka zwiększymy trzykrotnie, a długość promienia zmniejszymy trzy razy, to objętość nowego stożka:
A.zwiększy się trzy razy
B.zmniejszy się trzy razy
C.zmniejszy się dziewięć razy
D.nie zmieni się
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest
A.sześć razy dłuższa od wysokości walca
B.trzy razy dłuższa od wysokości walca
C.dwa razy dłuższa od wysokości walca
D.równa wysokości walca
Kąt wycinka będący powierzchnią boczną stożka jest równy \(186^\circ \), a tworząca jest o \(4\ \text{cm}\) dłuższa od promienia podstawy bryły. Oblicz pole powierzchni całkowitej oraz objętość stożka.
Kąt rozwarcia stożka ma miarę \(120^\circ \), a tworząca tego stożka ma długość \(4\). Objętość tego stożka jest równa
A.\( 36\pi \)
B.\( 18\pi \)
C.\( 24\pi \)
D.\( 8\pi \)
Kąt rozwarcia stożka ma miarę \(120^\circ \), a tworząca tego stożka ma długość \(6\). Promień podstawy stożka jest równy
A.\( 3 \)
B.\( 6 \)
C.\( 3\sqrt{3} \)
D.\( 6\sqrt{3} \)
Dany jest stożek o wysokości \(4\) i średnicy podstawy \(12\). Objętość tego stożka jest równa
A.\( 576\pi \)
B.\( 192\pi \)
C.\( 144\pi \)
D.\( 48\pi \)
Dany jest stożek o wysokości \(6\) i tworzącej \(3\sqrt{5}\). Objętość tego stożka jest równa
A.\( 36\pi \)
B.\( 18\pi \)
C.\( 108\pi \)
D.\( 54\pi \)
Stożek o promieniu podstawy \(r\) i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A.\( \frac{4}{3} \)
B.\( 12 \)
C.\( \sqrt{17} \)
D.\( 4 \)
Kąt rozwarcia stożka jest równy \(30^\circ \), a tworząca tego stożka ma długość \(8\) cm. Pole przekroju osiowego tego stożka wynosi:
A.\( 64\ \text{cm}^2 \)
B.\( 32\ \text{cm}^2 \)
C.\( 16\ \text{cm}^2 \)
D.\( 16\sqrt{3}\ \text{cm}^2 \)
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości \(12\). Wysokość stożka jest równa \(8\). Oblicz pole powierzchni bocznej tego stożka. 

Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest ćwiartką koła o promieniu \(8\) cm. Oblicz wysokość tego stożka.
W stożku stosunek pola powierzchni bocznej do pola podstawy jest równy \(\frac{3}{2}\). Oblicz sinus kąta między tworzącą a płaszczyzną podstawy tego stożka.
W stożku różnica długości tworzącej i promienia podstawy jest równa \(6\). Cosinus kąta \(\alpha \) między tworzącą a płaszczyzną podstawy tego stożka jest równy \(\frac{2}{5}\). Oblicz pole powierzchni bocznej tego stożka.
Dany jest stożek o objętości \(8\pi \), w którym stosunek wysokości do promienia podstawy jest równy \(3:8\). Oblicz pole powierzchni bocznej tego stożka.
Tworząca stożka ma długość \( 17 \), a wysokość stożka jest krótsza od średnicy jego podstawy o \( 22 \). Oblicz pole powierzchni całkowitej i objętość tego stożka.
Tworząca stożka o kącie rozwarcia \(\alpha \) ma długość \(8\). Pole powierzchni całkowitej tego stożka jest równe \(48\pi\). Oblicz objętość stożka oraz miarę kąta \(\alpha \).
Metalowy stożek, którego tworząca o długości \(10\) jest nachylona do płaszczyzny podstawy pod kątem \(30^\circ \), przetopiono na sześć jednakowych kulek. Oblicz promień kulki.
Stożek przecięto płaszczyzną równoległą do podstawy i dzieląca wysokość stożka w stosunku \(1:3\) licząc od podstawy stożka. Oblicz stosunek objętości otrzymanych brył.
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest ćwiartką koła o promieniu \(6\) cm . Oblicz wysokość tego stożka.
Poziom rozszerzony
Dany jest stożek, którego powierzchnia boczna jest \(2\) razy większa od pola jego podstawy. Kąt rozwarcia tego stożka oznaczmy literką \(\alpha \). Wykaż, że suma miejsc zerowych funkcji \(f(x)=(x - \operatorname{tg}^2 \alpha)(x-2) \) jest liczbą pierwszą.
Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru \(V = \frac{1}{3} \pi H (r^2 + rR + R^2)\), gdzie \(r\) i \(R\) są promieniami podstaw (\(r \lt R\)), a \(H\) jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa \(10\), objętość \(840\pi\), a \(r = 6\). Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw. 

Tematy nadrzędne i sąsiednie
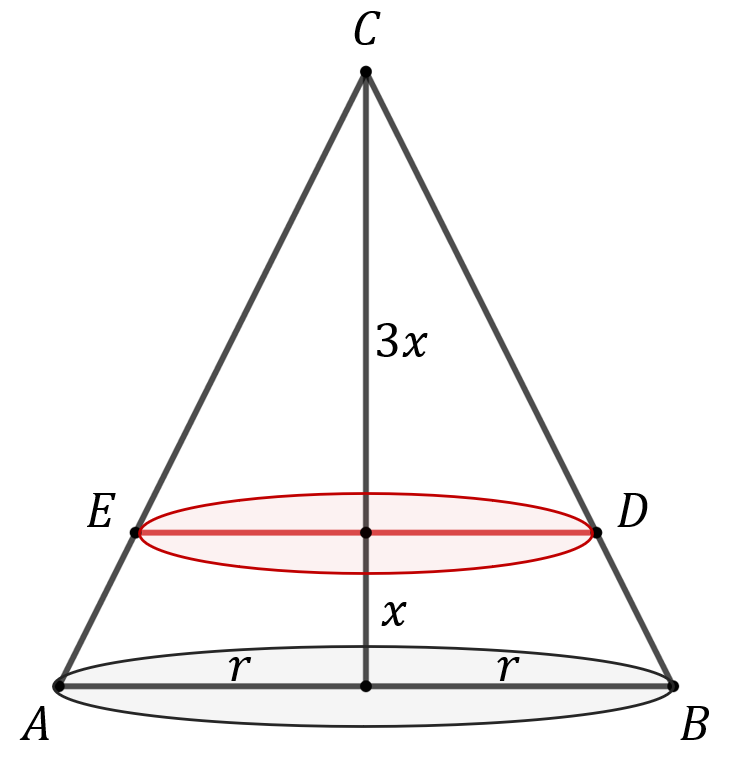 Podpiszmy promień podstawy \(r\). Wysokość całego stożka to \(4x\). Wówczas objętość stożka \(ABC\) to: \[V = \frac{1}{3} \pi r^2 \cdot 4x.\] Stożek o przekroju \(DCE\) jest podobny do stożka o przekroju \(ABC\) w skali podobieństwa: \[ k = \frac{3x}{4x} = \frac{3}{4}. \] Przy skali podobieństwa \(k\) objętości figur podobnych są w stosunku \(k^3\). Zatem objętość mniejszego stożka \(DCE\) wynosi: \[ V_1 = k^3\cdot V = \left(\frac{3}{4}\right)^3 V = \frac{27}{64}V. \] Objętość ściętego stożka \(ABDE\), to: \[ V_2 = V - V_1 = V - \frac{27}{64}V = \frac{37}{64}V. \] Zatem stosunek objętości tych dwóch brył to: \[ \frac{V_1}{V_2} = \frac{27}{64} : \frac{37}{64} = \frac{27}{37}. \]
Podpiszmy promień podstawy \(r\). Wysokość całego stożka to \(4x\). Wówczas objętość stożka \(ABC\) to: \[V = \frac{1}{3} \pi r^2 \cdot 4x.\] Stożek o przekroju \(DCE\) jest podobny do stożka o przekroju \(ABC\) w skali podobieństwa: \[ k = \frac{3x}{4x} = \frac{3}{4}. \] Przy skali podobieństwa \(k\) objętości figur podobnych są w stosunku \(k^3\). Zatem objętość mniejszego stożka \(DCE\) wynosi: \[ V_1 = k^3\cdot V = \left(\frac{3}{4}\right)^3 V = \frac{27}{64}V. \] Objętość ściętego stożka \(ABDE\), to: \[ V_2 = V - V_1 = V - \frac{27}{64}V = \frac{37}{64}V. \] Zatem stosunek objętości tych dwóch brył to: \[ \frac{V_1}{V_2} = \frac{27}{64} : \frac{37}{64} = \frac{27}{37}. \] 