Układy równań w zadaniach z treścią
Poziom podstawowy
Dany jest prostokąt o bokach długości \(a\) i \(b\), gdzie \(a\gt b\). Obwód tego prostokąta jest równy \(30\). Jeden z boków prostokąta jest o \(5\) krótszy od drugiego.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F i wpisz te litery w wykropkowanych miejscach.
Zależności między długościami boków tego prostokąta zapisano w układach równań oznaczonych literami: ……… oraz ……… . A.\( \begin{cases} 2ab=30 \\ a-b=5 \end{cases} \)
B.\( \begin{cases} 2a+b=30 \\ a=5b \end{cases} \)
C.\( \begin{cases} 2(a+b)=30 \\ b=a-5 \end{cases} \)
D.\( \begin{cases} 2a+2b=30 \\ b=5a \end{cases} \)
E.\( \begin{cases} 2a+2b=30 \\ a-b=5 \end{cases} \)
F.\( \begin{cases} a+b=30 \\ a=b+5 \end{cases} \)
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości \(a\) i \(b\) jest równy \(60\). Jeden z boków tego prostokąta jest o \(10\) dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
Obwód prostokąta o bokach długości \(a\) i \(b\) jest równy \(60\). Jeden z boków tego prostokąta jest o \(10\) dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A.\( \begin{cases} 2(a+b)=60 \\ a+10=b \end{cases} \)
B.\( \begin{cases} 2a+b=60 \\ 10b=a \end{cases} \)
C.\( \begin{cases} 2ab=60 \\ a-b=10 \end{cases} \)
D.\( \begin{cases} 2(a+b)=60 \\ 10a=b \end{cases} \)
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew.
Po roku stwierdzono, że uschło \(5 \%\) drzew w pierwszym sadzie i \(10 \%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(60 \%\) liczby drzew, które pozostały w pierwszym sadzie.
Niech \(x\) oraz \(y\) oznaczają liczby drzew posadzonych - odpowiednio - w pierwszym i drugim sadzie.
Po roku stwierdzono, że uschło \(5 \%\) drzew w pierwszym sadzie i \(10 \%\) drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano.
Liczba drzew, które pozostały w drugim sadzie, stanowiła \(60 \%\) liczby drzew, które pozostały w pierwszym sadzie.
Niech \(x\) oraz \(y\) oznaczają liczby drzew posadzonych - odpowiednio - w pierwszym i drugim sadzie.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby \(x\) drzew posadzonych w pierwszym sadzie oraz liczby \(y\) drzew posadzonych w drugim sadzie, jest A.\(\left\{\begin{array}{l}x+y=1960 \\ 0,6 \cdot 0,95 x=0,9 y\end{array}\right.\)
B.\(\left\{\begin{array}{l}x+y=1960 \\ 0,95 x=0,6 \cdot 0,9 y\end{array}\right.\)
C.\(\left\{\begin{array}{l}x+y=1960 \\ 0,05 x=0,6 \cdot 0,1 y\end{array}\right.\)
D.\(\left\{\begin{array}{l}x+y=1960 \\ 0,4 \cdot 0,95 x=0,9 y\end{array}\right.\)
Dane są dwie przecinające się proste. Miary kątów utworzonych przez te proste zapisano za pomocą wyrażeń algebraicznych (zobacz rysunek). 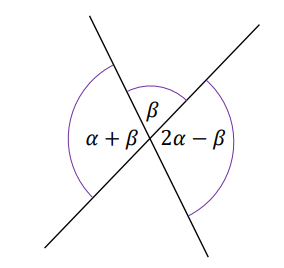
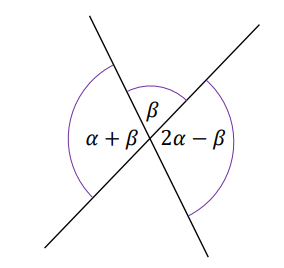
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ A.\( \begin{cases} (\alpha +\beta )+\beta =90^\circ \\ \alpha +\beta =2\alpha -\beta \end{cases} \)
B.\( \begin{cases} (\alpha +\beta )+\beta =180^\circ \\ \alpha +\beta =2\alpha -\beta \end{cases} \)
C.\( \begin{cases} (\alpha +\beta )+\beta =180^\circ \\ \beta =2\alpha -\beta \end{cases} \)
D.\( \begin{cases} \alpha +\beta =90^\circ \\ \beta =2\alpha -\beta \end{cases} \)
E.\( \begin{cases} \alpha +\beta =2\alpha -\beta \\ 180^\circ -(2\alpha -\beta )=\beta \end{cases} \)
F.\( \begin{cases} 3\alpha +2\beta =360^\circ \\ 2\alpha -\beta =2\beta \end{cases} \)
Jeśli od cyfry dziesiątek liczby trzycyfrowej odejmiemy cyfrę jedności, to otrzymamy \(6\). Suma cyfry dziesiątek i cyfry jedności tej liczby wynosi \(10\). Znajdź wszystkie liczby trzycyfrowe podzielne przez \(3\) spełniające ten warunek.
W pewnej szkole pracuje \(20\) nauczycieli. Stosunek liczby mężczyzn do liczby kobiet jest równy \(1 : 9\). Ile kobiet i ilu mężczyzn pracuje w tej szkole?
W dwóch naczyniach jest pewna ilość wody. Gdyby z pierwszego naczynia wylano do zlewu \(5\) cm3, to woda zawarta w tym naczyniu stanowiłaby połowę ilości wody znajdującej się w drugim naczyniu. Gdyby z drugiego naczynia przelano \(10\) cm3 wody do pierwszego naczynia, to ilości wody w obu naczyniach byłyby równe. Ile cm3 wody znajduje się w tych naczyniach?
Suma trzech liczb naturalnych jest równa \(42\). Druga liczba stanowi \(75\%\) pierwszej liczby. Trzecia liczba jest piątą częścią sumy pozostałych liczb. Znajdź te liczby.
Oblicz wymiary narysowanego poniżej prostokąta. 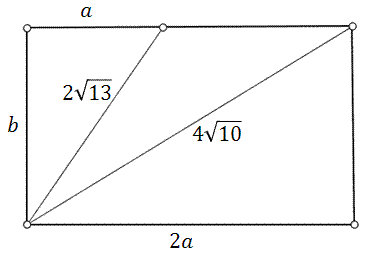

Tematy nadrzędne i sąsiednie